Тема 2. Информационные характеристики.

2.1. Количество информации в сообщении.

Основой любой теории является задание того эталона (меры), с помощью которого оцениваются изучаемые явления (процессы, объекты). В теории информации, где объектом исследования служит процесс передачи сообщений, ключевым является понятие количества информации, содержащейся в сообщении. Аксиомы количества информации вполне естественны и адекватны интуитивному пониманию терминов "информация" и "информативность":

– количество информации в сообщенииxнеотрицательно: ;

– количество информации убывает с ростом предсказуемости (вероятности) сообщения, находясь во взаимно-однозначной зависимости от последней: ;

– количество информации аддитивно, т.е. пара независимых сообщений и содержит количество информации, равное сумме количеств информации в каждом из них: .

Убедимся, что трех перечисленных аксиом достаточно для однозначного определения искомой меры как логарифма вероятности сообщения. Пусть XиY – два независимых ансамбля, где и – два сообщения. Пусть .Тогда ,где учтена независимость источниковXиY. С другой стороны, согласно требованию аддитивности .Нетрудно убедиться, что среди непрерывных функций единственной, удовлетворяющей свойству аддитивности ,является однородная линейная функция , гдеk– фиксированный коэффициент. Ограничиваясь дифференцируемыми функциями, это легче всего показать, продифференцировав обе части условия аддитивности поvпри и получив равенство , а значит, .

Таким образом, количество информации в конкретном сообщении

, (2.1)

где учтено также требование неотрицательности I(x).

Основание, по которому берется логарифм в последнем выражении, задает лишь масштаб, а, следовательно, единицу измерения количества информации. Наиболее часто употребляется логарифм по основанию 2, и в этом случае единицу измерения количества информации называют «бит» (от английского «binarydigit»). Иногда используют натуральный или десятичный логарифмы, называя соответствующие им единицы «нат» и «дит».

В дальнейшем изложении под обозначением logбудет пониматься двоичный логарифм, а количество информации измеряться в битах. Например, если , то бит.

2.2. Энтропия дискретного источника.

Пусть имеется дискретный источник с ансамблем Xи известными вероятностями сообщений . Количество информации, содержащееся в каждом сообщении, определится величиной. Вследствие случайности самого сообщения количество информации в немпредставляет собой случайную величину. Поэтому для описания источника в целом естественно использовать среднее количество информации, приходящееся на одно сообщение.

Математическое ожидание H(X) количества информацииI(x) в сообщении дискретного источника называетсяэнтропией источникаи определяется выражением

(2.2)

Подставив в (2.2) выражение (2.1), получим

(2.3)

Замечание.Согласно соотношению (2.1) количество информации I(x) стремится к бесконечности для тех сообщений , вероятность появления которых близка к нулю. Однако энтропия любого дискретного источника всегда конечна, поскольку стремится к нулю при , в чем легко убедиться с помощью правила Лопиталя.

Поскольку количество информации I(x) отражает степень неожиданности сообщения, энтропия источника (ансамбля), как математическое ожиданиеI(x), характеризует среднюю неожиданность или непредсказуемость состояний источника.

Рассмотрим основные свойства энтропии.

1. Энтропия дискретного источника неотрицательна: , так как и . При этом, энтропия равна нулю тогда и только тогда, когда источник полностью предсказуем, т.е. выдает единственное наперед известное сообщение.

2. Пусть – мощность дискретного источника сообщений с ансамблемX, т. е. тогда

, (2.4)

причем верхняя граница достигается в том и только том случае, когда сообщения источника равновероятны.

Доказательство.Справедливость левого неравенства уже установлена. Доказательство правого основывается на часто используемом в теории информации логарифмическом неравенстве

, (2.5)

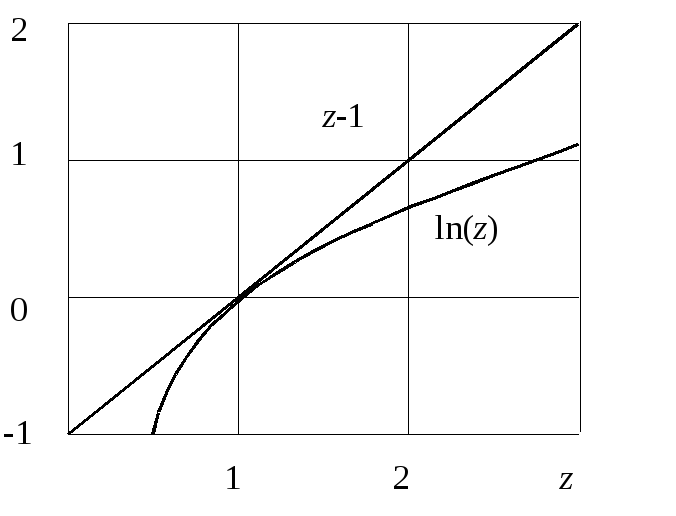
равенство в котором имеет место только при . Формальная проверка его справедливости не составляет труда, однако нагляднее воспользоваться графиком, представленным на рис. 2.1 и не требующим пояснений.

Рис. 2.1

Рассмотрим разность

где учтено, что

Тогда используя (2.5), получаем

откуда и следует правое неравенство в (2.4).

Поскольку равенство в (2.5) имеет место только при , то и в (2.4) оно достигается тогда, когда а значит, для всех , т. е. при равновероятных сообщениях.

Замечание.Установленные границы энтропии хорошо согласуются с ее ролью меры неопределенности сообщений источника. В самом деле, когда источник не обладает вообще никакой неопределенностью, энтропия обращается в нуль. Максимальной же неопределенностью, очевидно, обладает источник, все сообщения которого равно ожидаемы, т.е. априори не имеют предпочтений друг перед другом по вероятности появления.

3. Пусть XиY– статистически независимые ансамбли, аXY– ансамбль, сообщения которого представляют собой все возможные пары , где , , т. е. образуют множество . ПосколькуXиYнезависимы, то и

. (2.6)

Рис. 2.2.

Данное свойство, называемоеаддитивностьюэнтропии, означает, что при комбинировании независимых источников их энтропии складываются.

Соотношение (2.6) можно обобщить на произвольное число независимых источников. Пусть – ансамбль, образованныйnстатистически независимыми ансамблями так, что каждое сообщение из есть цепочка , где . Тогда

Пример 2.2.1.Рассмотрим двоичный источник, сообщения которого имеют вероятности , . Энтропия подобного ансамбля

. (2.7)

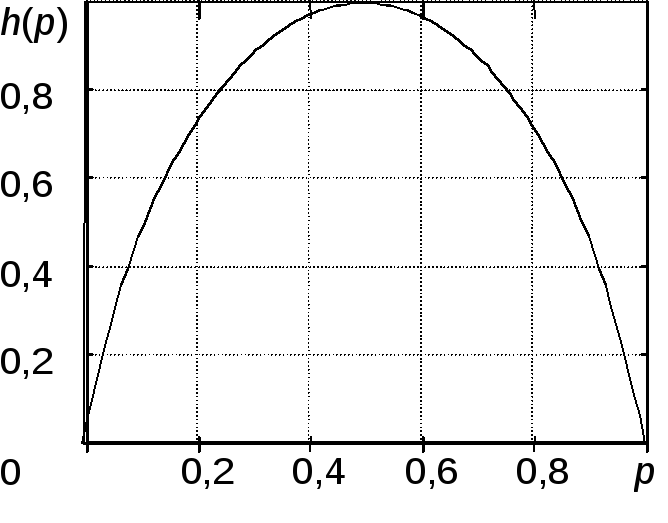
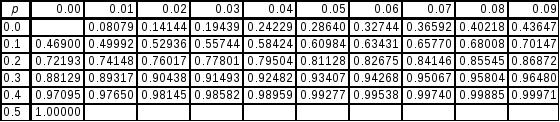
Введенная функция – энтропия двоичного источника – чрезвычайно популярна в теории информации. График ее представлен на рис. 2.2. В точках и эта функция обращается в нуль. При , когда оба сообщения равновероятны, она имеет максимум, равный единице, т.е. одному биту. Значения даются табл. 2.1.

Таблица 2.1.

Энтропия двоичного ансамбля