Коваленко Л.И. Элементы векторного анализа

Министерство образования Российской Федерации

Московский физико-технический институт Кафедра высшей математики

Методические указания

по математическому анализу для студентов второго курса

ЭЛЕМЕНТЫ

ВЕКТОРНОГО АНАЛИЗА

Второе издание

Москва 2001

Составитель: Л.И.Коваленко

УДК 517

Методические указания по математическому анализу для студентов второго курса. Элементы векторного анализа. МФТИ, 2001.

Излагаются основные понятия векторного анализа, формулы Остроградского–Гаусса и Стокса, приемы набла-техники. Доказываются первая и вторая формулы Грина в пространстве. Все демонстрируется на задачах, решение которых приводится. Система координат предполагается декартовой прямоугольной, причем правой.

В настоящее издание добавлено несколько задач, требующих умения работать с терминами поля как в векторной, так и в координатной форме. Внесены другие изменения.

Автор выражает глубокую благодарность чл.-корр. РАН Л.Д. Кудрявцеву, проф. М.И. Шабунину, чл.-корр. РАО Г.Н. Яковлеву, чьи отличные лекционные курсы математического анализа послужили основой для написания данного учебного пособия.

Автор благодарит О.А.Пыркову и Д.А.Терешина за предложения и замечания, которые были учтены при подготовке этого издания.

ОГЛАВЛЕНИЕ

§ 1.	Скалярные и векторные поля. Производная по напра-
§ 2.	влению и градиент скалярного поля . . .	. . . . . . .	4
	Дивергенция и поток векторного поля.	Формула
§ 3.	Остроградского–Гаусса в терминах поля	. . . . . . .	7
	Соленоидальные векторные поля . . . . .	. . . . . . .	14

§4. Циркуляция векторного поля. Потенциальные век-

торные поля . . . . . . . . . . . . . . . . . . . . . . . . 18

§5. Ротор векторного поля. Формула Стокса в терминах поля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

Механический смысл ротора . . . . . . . . . . . . . . . 20

§6. Однократное применение оператора Гамильтона . . . 26

Правила работы с r . . . . . . . . . . . . . . . . . . .	27
Градиент одного вектора по другому . . . . . . . . . .	29
§ 7. Повторное применение оператора Гамильтона . . . .	32
Формулы Грина в R3 . . . . . . . . . . . . . . . . . . .	34
Список литературы . . . . . . . . . . . . . . . . . . . .	36

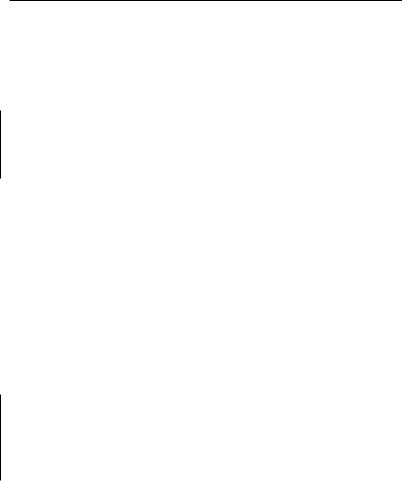
4Л.И. Коваленко. Элементы векторного анализа

§1. Скалярные и векторные поля. Производная по направлению и градиент скалярного поля

Определение 1. Говорят, что в области G задано скалярное (или векторное) поле, если каждой точке M G поставлено в соответствие некоторое число F (M) (или век-

тор a(M)).

Поле температуры внутри некоторого нагретого тела

— это скалярное поле. Поле гравитационное — векторное поле.

Если дано некоторое скалярное или векторное поле в области G R3, то, введя систему координат, можно представить скалярное поле в виде некоторой функции F (x, y, z), а векторное поле — в виде вектор-функции a = = (P (x, y, z), Q(x, y, z), R(x, y, z)).

Пусть в области G R3 задано скалярное поле f(M). Проведем луч через точку M0 G в направлении век-

тора l, |l| = 1.

Определение 2. Производной скалярного поля f в точке M0 по направлению l называется предел

∂f		f(M)	f(M0)		→
					M M = tl, t > 0, (1)
	(M0) = lim	−	,
∂l					−−−−0
	t→+0	t

если он существует.

Введя систему координат, представим заданное скалярное поле в виде функции f(x, y, z).

Величину, задаваемую формулой (1), называют произ-

водной функции f(x, y, z) по направлению l. Утверждение 1. Если функция f(x, y, z) в точке M0

дифференцируема, то она в этой точке имеет производную по любому направлению l и эта производная находится по формуле

			§ 1. Скалярные и векторные поля					5
	∂f	(M0) =	∂f	(M0) cos α+	∂f	(M0) cos β +	∂f	(M0) cos γ, (2)
	∂l		∂x		∂y		∂z

где cos α, cos β, cos γ — направляющие косинусы вектора l.

Пусть функция f(x, y, z) дифференцируема в области G.

Определение 3. Вектор ∂f∂x , ∂f∂y , ∂f∂z называется

градиентом скалярного поля f, или градиентом функции f(x, y, z), и обозначается grad f.

Операцию перехода от скалярного поля f к grad f обозначают, следуя Гамильтону, символом r (читается «на-

бла») и называют оператором «набла», или оператором

Гамильтона. Таким образом, по определению
		rf = grad f.	(3)
Формулу (2) можно переписать в следующем виде, учи-
тывая, что |l| = 1:
	∂f
		(M0) = (l, rf) = |rf| cos ϕ,	(4)
	∂l

где ϕ — угол, образованный l и grad f в точке M0. Отсюда следует, что если | grad f(M0)| 6= 0, то в точке M0 производная функции f по направлению достигает наибольшего значения только по направлению grad f (cos ϕ = 1), при этом

∂f

max ∂l (M0) = |rf(M0)|.

Итак, в каждой точке, в которой | grad f| не равен нулю, направление grad f — это направление наибольшего роста f (оно единственно), а длина его равна скорости возрастания f по этому направлению.

Если | grad f| = 0 в данной точке, то в этой точке производные функции f по всем направлениям равны нулю.

Таким образом, установлено, что градиент скалярного поля зависит лишь от самого поля, но не от выбора системы координат.

Пусть |rf(M0)| 6= 0. Пусть f(x, y, z) = C — поверх-

6Л.И. Коваленко. Элементы векторного анализа

ность уровня в точке M0. Уравнение касательной плоскости в точке M0 к этой поверхности имеет вид

∂f	(M0)(x−x0) +	∂f	(M0)(y −y0) +	∂f	(M0)(z −z0) = 0. (5)
∂x		∂y		∂z

Из этого равенства следует, что если | grad f| в точке не равен нулю, то grad f направлен по нормали к поверхности уровня, проходящей через эту точку.

Все изложенное переносится на случай плоского скалярного поля. Соответственно в формуле (2) будет два слагаемых, в уравнении (5) — тоже. Это — уравнение касательной к линии уровня в точке M0.

2		2		2
Задача 1. Для функции Φ =	x	+	y	+	z	найти произ-
	2		2		2
	a		b		c

водную по направлению внутренней нормали к цилиндрической поверхности x2 + z2 = a2 + c2 в точке M0(a, b, c).

Р е ш е н и е. Пусть f(x, y, z) = x2 + z2. Данная в условии поверхность — это поверхность уровня для f, проходящая через точку M0. Имеем

rf(M0) = (2a, 0, 2c).

Функция f в точке M0 растет быстрее всего по направлению grad f, значит, по направлению нормали к заданной поверхности. Исходя из вида функции f, заключаем, что это — направление внешней нормали. Следовательно, единичный вектор внутренней нормали в точке M0 будет

l =

−2a

, 0,

−2c

=

−a

, 0,

−c

.

√4a2 + 4c2

√4a2 + 4c2

√a2 + c2

√a2 + c2

Имеем rΦ =

2x

,

2y

,

2z

. По формуле (4) получаем

a2

b2

c2

∂Φ

a

2a

c

2c

4

(M0) = −

√

·

−

√

·

= −

√

.

∂l

a2

c2

a2 + c2

a2 + c2

a2 + c2

О т в е т. − √ 4 . a2 + c2

Задача 2. Пусть a — постоянный вектор, |a| 6= 0, r —

§ 2. Дивергенция и поток. Формула Остроградского–Гаусса 7

радиус-вектор произвольной точки M R3, проведенный из фиксированной точки O. Найти grad |[r, a]|3.

Р е ш е н и е. Введем декартову прямоугольную правую

a

систему координат 0, i, j, k, k = |a|. Тогда имеем a = (0, 0, |a|), r = xi + yj + zk,

i j k

[r, a] = x y z = |a|(yi − xj),

0		a
|[r, a]| = |a|(x2 + y02)1/2,	|	||[r, a]|3 = |a|3(x2 + y2)3/2.

Далее находим (см. определение 3)

grad |[r, a]|3 = 3|a|3(x2 + y2)1/2(xi + yj) = 3|a|2|[r, a]|(r − zk).

А так как z = (r, k) = r,	a	, то получим
	|a|				|a|	=
grad |[r, a]|3 = 3|a|2 |[r, a]| r −			r, |a|
				a	a

= 3 |[r, a]| (r (a, a) − a (a, r)) .

Используя формулу для двойного векторного произведения [A, [B, C]] = B (A, C) − C (A, B), окончательно получаем grad |[r, a]|3 = 3 |[r, a]| [a, [r, a]] .

От в е т. 3 |[r, a]| [a, [r, a]].

§2. Дивергенция и поток векторного поля. Формула Остроградского–Гаусса

втерминах поля

Определение 4. Пусть в области G R3 задано векторное поле a = (P, Q, R) с непрерывно дифференцируемыми компонентами.

Дивергенцией векторного поля a называется скалярная функция

8Л.И. Коваленко. Элементы векторного анализа

div a =

∂P

+

∂Q

+

∂R

.

∂x

∂y

∂z

Задача

3. а)

Вычислить

div(grad f(r)),

где r

=

=

x2 + y2 + z2

, f(r) — дважды непрерывно дифферен-

цируемая функция

.

б

)

В каком случае

div grad f(r) = 0?

p

Р е ш е н и е. а) Вычислим grad f(r) = (P, Q, R). Имеем

∂f(r)

x

r

P =

= f0(r) ·

grad f = f0(r) ·

,

(6)

∂x

r

r

где r — радиус-вектор точки (x, y, z).

Для вычисления div grad f найдем вначале

∂P

. Имеем

∂x

∂P

f0

f00

f0

=

+ x2

−

.

∂x

r

r2

r3

Заменяя в полученном выражении x последовательно на

y, потом на z, получаем аналогичные формулы для

∂Q

,

∂y

∂R

∂z

∂P

∂Q

∂R

f0

div grad f(r) =

+

+

= f00

+ 2

.

∂y

∂z

∂x

r

б) Решаем дифференциальное уравнение

f0

u

du

dr

C0

f00

+2

= 0, f0 = u, u0

+2

= 0,

= −2

, f

0 = u =

.

r

r

u

r

r2

f =

C1

+ C2, Ci

= const, i = 0, 1, 2;

r

(7)

div grad

C

= 0.

1

+ C2

r

О т в е т.

а) f

00 + 2

f0

; б) f =

C1

+ C2, Ci — любые

r

постоянные, i = 1, 2.

r

Определение 5. Пусть в области G R3

задано век-

торное поле a = (P, Q, R) с непрерывными компонентами. Пусть S — ориентированная кусочно-гладкая поверхность, лежащая в области G, ν — единичный вектор нормали к поверхности, задающей ее ориентацию. Интеграл

§ 2. Дивергенция и поток. Формула Остроградского–Гаусса 9

ZZ

(a, ν) ds

S

называется потоком векторного поля a через поверхность S и обозначается

ZZ

a ds.

S

Имеем

ZZ ZZ ZZ

ads = (a, ν) ds = (P cos α+Q cos β +R cos γ) ds, (8)

S S S

где cos α, cos β, cos γ — направляющие косинусы нормали ν к поверхности S, задающей ее ориентацию.

Напомним, что система координат правая.

Пусть S — гладкая поверхность, имеющая явное пред-

ставление z = f(x, y), (x, y) D, D — область на плоско-

сти переменных x, y.		Тогда поверхность S имеет векторное
представление r = r(x, y) = (x, y, f(x, y)), (x, y)							.
						D
Отметим, что угол между вектором
	[rx, ry]	1
n =		=			(−fx, −fy, 1)
	|[rx, ry]|		q
				1 + fx2 + fy2

и вектором k = (0, 0, 1) острый.

Если вектор ν (см. (8)) совпадает с вектором n, то вычисление интеграла

ZZ

R cos γ ds

S

в силу того, что
	1
		+ fy2	q
	1 + fx2
cos γ =			, ds = 1 + f2		+ f2 dx dy,
	q			x	y

сводится к вычислению такого двойного интеграла по области D:

10

Л.И.

Коваленко. Элементы векторного анализа

ZZ

R cos γ ds =ZZ R(x, y, f(x, y)) dx dy.

S

D

Аналогично получаются формулы для вычисления ин-

тегралов

S P cos α ds и

S Q cos β ds (см. (8)) в случае яв-

ного

представления поверхности

S

в виде

x = ϕ(y, z) —

для

RR

RR

первого интеграла и в виде y = ψ(x, z) — для второго.

z

Задача 4. Вычислить поток векторного поля

a = (z2 − x, 1, y5)

3

~ν

y

через

ориентированную внутренней

S1

нормалью поверхность S:

y2

=

2x,

S

отсеченную плоскостями: x = 2, z =

S2

= 0, z = 3.

Р е ш е н и е.

Согласно

фор-

0

2

x

муле (8):

Рис. 1

ZZ a ds =ZZ

(z2

− x) cos α+

S

S

+ cos β + y5 cos γ

ds,

где cos α, cos β, cos γ — направляющие косинусы

внутрен

-

ней нормали к S. Имеем

ZZ cos β ds =ZZ cos β ds +ZZ cos β ds,

(9)

S

S1

S2

где (см. рис. 1) S1, S2 — части поверхности S, расположенные соответственно при y>0 и y60, S = S1 S2; cos β > 0

zна S2 и отличается лишь знаком

3от cos β в симметричных относи-

тельно плоскости (x, z) точках на

Dповерхности S1. Поэтому из (9)

						следует, что
-	2	0	2		y
		Рис. 2				ZZ cos β ds = 0.

S