
1.Числовой ряд, его сход-ть.
Определение:
Формально записанная сумма бесконечного
мн-ва чисел![]() (1) наз-ся числовым рядом. Если послед-ть
его частичных сумм{Sn}:
S1=a1,
S2=a1+a2,
,..., Sn=a1+...+an=
(1) наз-ся числовым рядом. Если послед-ть
его частичных сумм{Sn}:
S1=a1,
S2=a1+a2,
,..., Sn=a1+...+an=![]() ...
имеет конечный пределlim
Sn=S,
то говорят, что ряд (1) сходится и имеет
суммуS(в этом случае
запись (1) не просто формальная запись,
а выражает число). Еслиlim Snне существует или бесконечен, то говорят,
что ряд расходится (в этом случае (1) не
выражает никакого числа, но еслиlim
Sn=,
то ряду (1)приписывают сумму
бесконечности).
...
имеет конечный пределlim
Sn=S,
то говорят, что ряд (1) сходится и имеет
суммуS(в этом случае
запись (1) не просто формальная запись,
а выражает число). Еслиlim Snне существует или бесконечен, то говорят,
что ряд расходится (в этом случае (1) не
выражает никакого числа, но еслиlim
Sn=,
то ряду (1)приписывают сумму
бесконечности).
2.T-ма ( Критерий Коши сход-ти ряда).
[ряд
(1) сходится]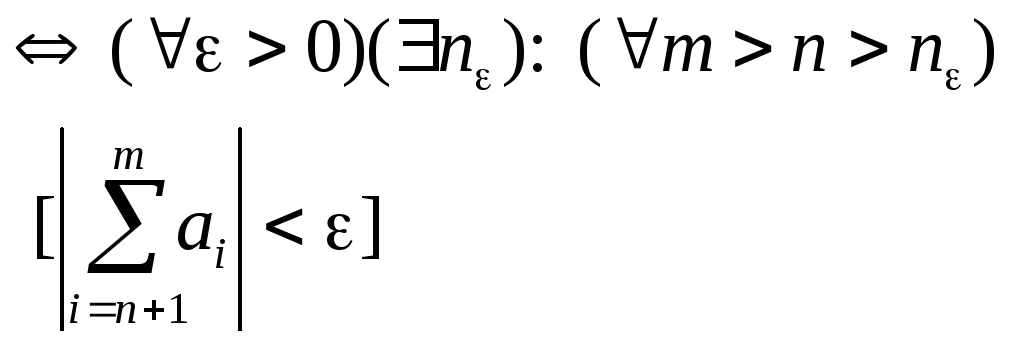
(при достаточно больших номерах любой отрезок ряда делается сколь угодно малым по модулю).
Сходимость ряда
(1) равносильно сход-ти послед-ти частичных
сумм {Sn},
а сход-ть послед-ти равносильна выполнению
критерия Коши для послед-ти:![]() ,
где
,
где
![]()
3.Определение:Ряд![]() наз-сяk-ым остатком ряда.
Если этот ряд сход-ся, то его сумму
обозначают
наз-сяk-ым остатком ряда.
Если этот ряд сход-ся, то его сумму
обозначают![]() .
.
Т-ма (о сход-ти остатка ряда)
k-ый остаток ряда сход-ся или расход-ся одновременно с самим рядом. В случае сход-ти суммаS=Sk+r k (k-ая частичная сумма плюс сумма k-го остатка ряда)
При достаточно больших номерах (>k)ряд и его k-ый остаток имеют одинаковые отрезки ряда, поэтому критерий Коши для них выполняется или не выполняется одновременно так, что сам ряд и его остаток сход-ся или расход-ся одновременно. Пусть ряд (1) сход-ся:
lim Sn= S R,тогда при n>kбудетn=k+m, гдеm- некоторое натуральное числоSn=a1+a2+...+ak+ak+1+...+ak+m,где
m=ak+1+...+ak+m- m-ая частичная сумма остатка рядаak+1+ak+2+...+ak+m+... Приn Sn S, при этом m = n-k (к-фиксированное) и потомуlim m= r k (т.к. по условию остаток ряда сход-ся). В пределе получаемS=Sk+r k
4.Следствие о роли конечного числа членов ряда .
Отбрасывание, добавление или изменение конечного числа членов ряда не влияют на его сход-ть (влияют только на сумму в случае сход-ти)
При достаточно большом куказанные изменения не затрагиваютк-ый остаток ряда, ак-ый остаток ряда сходится или расходится одновременно с самим рядом
5.Т-ма (необходимые признаки сход-ти).
Если ряд (1) сходится, то:
1) n-ый член ряда стремится к нулю:lim an =0.
2)сумма k-ого остатка ряда, прик, стремится к нулю:lim r k=0
Пусть ряд (1) сходится, тогда:
1)lim Sn = S lim Sn-1 = S lim an = lim (Sn-Sn-1)= S - S = 0; 2) lim rk = т-ма о сход-ти ряда=lim(S-Sk)=S-lim Sk=S-S=0
Из т-мы следует, что если lim an0, то ряд расходится, но условиеlim an=0 не гарантирует сход-ти ряда (это только необходимый признак, но не достаточный)
Пример:Геометрический ряд.
b+bq+bq2+...+bqn-1+...=![]() сходится приq<1
и расходится приq1
Приq1
сходится приq<1
и расходится приq1
Приq1
![]() anне стремится
к0, чего не
может быть. Необходимый признак сход-ти
не выполнен ряд рассходится. Еслиq<1
anне стремится
к0, чего не
может быть. Необходимый признак сход-ти
не выполнен ряд рассходится. Еслиq<1
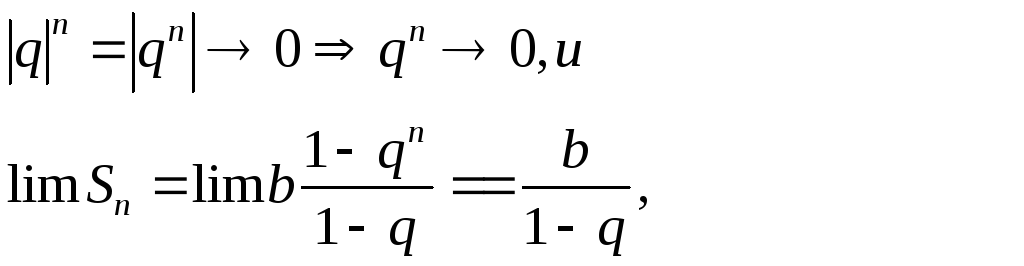 ряд
сходится и
ряд
сходится и![]()
Пример:Гармонический ряд.
![]() расходится, т.к.
расходится, т.к.
![]() , хотя необходимый признак выполнен:lim an=
, хотя необходимый признак выполнен:lim an=
![]()
6.Определение :Суммой рядов![]() anи
anи![]() bnи произведением
bnи произведением![]() anна числоназ-ся
ряды
anна числоназ-ся
ряды![]() (an+bn)
и
(an+bn)
и ![]() an.
an.
Т-ма о линейных операциях с рядами.
Если ряды![]() an
и
an
и ![]() bnсходятся, то их линейная комбинация
bnсходятся, то их линейная комбинация![]() (an+bn)cходится к линейной
комбинации сумм данных рядов:
(an+bn)cходится к линейной
комбинации сумм данных рядов:![]()
Пусть
![]() an=A,
an=A,
![]() bn=B,
т.е.A=
lim
bn=B,
т.е.A=
lim![]() ai,
B= lim
ai,
B= lim![]() bi
, тогда для
ряда
bi
, тогда для
ряда ![]() Сn=
Сn=![]() (an+bn)
сущ-ет С
= lim
(an+bn)
сущ-ет С
= lim![]() Ci
=
lim
Ci
=
lim![]() (ai+bi)
= для
конечной суммы распределитель- ный и
сочетательный законы верны
==
lim
(
(ai+bi)
= для
конечной суммы распределитель- ный и
сочетательный законы верны
==
lim
(![]() ai+
ai+![]() bi)
= A+B,
т.е.
bi)
= A+B,
т.е.![]() (an+bn)
=
(an+bn)
= ![]() an
+
an
+
![]() bn
Признаки сходимости положительных
рядов.
bn
Признаки сходимости положительных
рядов.
Если у ряда а1+а2+…+аn+… (1) все члены аn за исключением м.б. конеч. их числа имеют одинак. знак, то ряд наз-ся знакопостоянным : положительным - если аn 0 и отриц-м – если аn0.Т.к. отр. ряд можно получить из полож. умножением на –1, то дост. рассм. пол. ряды.
Теор Критерий сходимости положительного ряда.
Пол. ряд (1) сходится посл-ть его частичных сумм ограничена.
Ряд (1) сх-ся сх-ся посл. Част. Сумм {Sn}. У пол. ряда. Эта посл. Монотонно возр-ет (Sn+1=Sn+an+1,an+10 Sn+1 Sn), а монот.посл. сх-сяона ограничена
7.Теор Признак сравнения в форме нер-ва.
Если сущ ( n0): ( n>n0)[anbn], то из сх-ти ряда bnсх-ть рядаan, а из расх. рядаanрасх. р.bn.
Благодаря сл.1.5. можно счит., что нер-во вып-ся для всех номеров нач. с 1го (n)[anbn],
тогда
![]() ai
ai
![]() bi.
Если р.bnсх-ся, то по т.2.1. посл-ть его частич-х
сумм огр-на:
bi.
Если р.bnсх-ся, то по т.2.1. посл-ть его частич-х
сумм огр-на:
![]() biM
тогда из (*)
biM
тогда из (*)
![]() aiM,
т.е. посл. част-х сумм рядаanогран-на, а это по 2.1. означ. что р.anсх-ся. Если р.anрасх. то расх и р.bnт.к. в прот. Случ. По док-му сх-ся бы р.an.
aiM,
т.е. посл. част-х сумм рядаanогран-на, а это по 2.1. означ. что р.anсх-ся. Если р.anрасх. то расх и р.bnт.к. в прот. Случ. По док-му сх-ся бы р.an.
8.Теор Признак сравнения в пред форме.
Если сущ. Lim(an/bn)=kконеч. или бескон., то
при к=0; из сх-ти bnсх-тьan
при к=+; из расх-ти bnрасх-тьan
при 0<к<+; оба ряда сх-ся или расх. одновременно.
Док-во анал-но док-ву соотв. Пр-ку сравнения несоб. Инт-ов
9.Теор Признак Даламбера
Если сущ. lim(an+1)/an=D, то при D<1 ряд (1) сх-ся приD>1- расх-ся, причёмlim an=+
Если lim(an+1)/an<1, то (q>0):[ lim(an+1)/an<q<1].По сл-ию о сохр. нер-ва Т-6.5. нач. с нек. номераn будет (an+1)/an<q. Благод. 1.5. мож. Счит., что (n)[ (an+1)/an < q],знач.(n)[an+1<anq]a2<a1q,a3<a2q<(a1q)q=a1q2a3<a1q2…an<a1qn-1. Т.к. геом. р.a1qn-1 при 0<1сх-ся, то по пр-ку срав. Сх-ся рядan. Пустьlim(an+1)/an>1, тогда (q):[ lim(an+1)/an>q>1]. При дост. больших номрахnбудет (an+1)/an>qan+1>anq, мож. счит., что это верно при всех ном-хn, отсюда ан-но предыдущему получаемan>a1qn-1; ноlima1qn-1=+ liman=+, ряд расх-ся.
10.Теор Радикальный признак Коши.
Если lim
![]() =c,
то при с<1ряд сх-ся, приc>1- расх-ся, причёмliman=+
=c,
то при с<1ряд сх-ся, приc>1- расх-ся, причёмliman=+
Самост.
Ан-но теореме 2.4. Исп-ть
![]() ><qan><qn
><qan><qn
11.Теор Инт-й признак Коши.
Если члены ряда an являются знач-ми некот. неотр. убывающей ф-ииf(x), непрерывной на[1,+[: a1=f(1),a2=f(2),…,an=f(n),…, то ряд сх. Или расх. одноврем. с несоб. инт-ом(1to +)f(x)dx.
Сумма anвыраж. Площадь ступ. фигуры с беск. Основанием[0, +[, а (1to +)f(x)dx – пл-дь криволю трапеции с бескон основанием [1, +[ под графиком y=f(x). Утв-ся, что обе эти площади конеч. или бескон. одновременно.
Согл. критерию сх-ти несоб. инт-ла от неотр. ф-ии инт-л сх-сяФ(х)=(1to x)f(t)dtограничена на[1, +[, а согл. кр-ю сх-ти +го ряда, ряд an сх-ся посл-ть частич. Сумм {Sn} огр-на. Ввиду убывания f k<x<k+1f(k)f(x)f(x+1)akf(x)a k+1 (k to k+1)akdx(k to k+1)f(x)dx(k to k+1)a k+1dxak(k to k+1)f(x)dxa k+1 (k=1 to n)ak(k=1 to n) (k to k+1)f(x)dx(k=1 to n)a k+1 Sn(1 to n+1)f(x)dxSn+1-a1SnФ(n+1)Sn+1-a1.
Если (1 to +) сх-ся, то{Ф(n+1)} ограничена, тогда из нер-ва Sn+1Ф(n+1)+a1что{ Sn+1}
Ограничена и потому anсх-ся. Если же(1to +) расх-ся, то{Ф(n+1)} неограничена, а из нер-ва SnФ(n+1) {Sn}неограничена и потому ряд расх-ся
12.Пример
(1/n ) – наз-ся общим гармоническим рядом (Дирихле), сх-ся при>1 и расх. при1.
(1 to +)dx/x - сх-ся при>1 и расх. при 1. При >0ф-яf(x)=1/x будет убывающей, неотрицательной, непрерывной на[1, +[, причём f(n)=1/n=an. Поэт. Согл. 2.6. данный ряд сх-ся или расх. одноврем. с интегралом.
При <0an=1/n +, а пр=0an=11 anне0ряд расх-ся. Т.о. при всех -<1 ряд расх., при>1сх-ся.
14.Теор Об абсолютной сходимости.
Если сходится
![]() |an|,
то сх-ся и сам
|an|,
то сх-ся и сам
![]() an.
an.
[![]() |an|-сх-ся
](*крит
Коши*)(>0)(n ):(m>n>n)[|
|an|-сх-ся
](*крит
Коши*)(>0)(n ):(m>n>n)[|![]() |an||<
|an||<![]() |an|<].Но
|an|<].Но
![]() |an||
|an||![]() |an|(>0)(n):(m>n>n)[|
|an|(>0)(n):(m>n>n)[|![]() an|]<](*крит.
Коши*)
an|]<](*крит.
Коши*)![]() an
сх-ся.
an
сх-ся.
Определение
Если ряд
![]() |an|
сх-ся, то говорят, что ряд
|an|
сх-ся, то говорят, что ряд
![]() an
абс. сх-ся. Если сам ряд
an
абс. сх-ся. Если сам ряд
![]() an
сх-ся, а ряд
an
сх-ся, а ряд
![]() |an|
расх., то говорят, что
|an|
расх., то говорят, что
![]() an
сх-ся неабсолютно(условно).
an
сх-ся неабсолютно(условно).
13.Определение
Ряд у которого полож. члены чередуются через один наз-ся знакочередующимся. Для зн.ч. ряда им-ся свой дост. признак. сх-ти.
Теор Признак Лейбница
Если у зн.ч. ряда n-й член стремится к 0 монотонно убывая, то ряд сх-ся, сумма ряда им. знак 1го члена ряда и не превосх. его по модулю.
Пусть у зн.ч. ряда a1+a2-…-an+… lim |an|=0, |a1||a2||a3||an|=cn тогда ряд запис. в виде с1-с2+с3-… (1),еслиa10 и –с1+с2-с3+… (2) если а10.
а10. Для частич. сумм с чёт. номерамиn=2kимеемS2k=c1-c2+c3-c4+…+c2k-1-c2k=
{(c1-c2)+(c3-c4)+…+ c2k-1-c2k (3)
{c1-(c2-c3)-(c4-c5)-…-c2k (4). Т.к. с1с2…, то все скобки0, поэтому (3) S2k0, посл. {S2k} возрастает: S2k+2 = S2k+ (c2k+1-c2k+2) S2k. (4) S2kc1. Т.о.{S2k}возрастает и ограничена сверхуона имеет конеч.lim S, причём 0 S2kс10 Sс1.
Для посл-ти частич. сумм с неч. номерами n=2kимеемS2k-1=c1-c2+…+c2k-1=(c1-c2+…+c2k-1-c2k)+c2k=S2k+c2k
lim(k) S2k-1=(*по усл.lim(k) c2k=0*)= lim(k) S2k=S. Теперь покажем, что вся посл-ть{Sn} имеет предел S. Зададим>0. Тогдаlim(k) S2k=S(n1): (n=2kn1)[|Sn-S|<], аlim(k) S2k-1=S(n2):(n=2k-1n2)[|Sn-S|<]. Возьмёмn=max{n1,n2}. Тогда(n> n)[|Sn-S|<].Это означ. Чтоlim Sn=S. Т.о. данный ряд сх-ся к сумме S, причём 0Sc1(*a10c1=a1*)0sa1.Ан-но в случаеa10док-ся, что ряд сх-ся кS, причём –с1S0(*а10-с1=а1*)а1S0.Т.о.S и а1 имеют один знак, причём|S||a1|
Опр.Знакочер. ряд удовл. условиям признака Лейбница наз-ся рядом лейбницевского типа. Любой остаток ряда лейб. типа есть т.ж. ряд лейб. типа, поэт верно следствие:
Следствие Об остатке ряда лейб. типа.
Любой n-й остаток ряда л.типа имеет знак 1-го члена этого остатка (т.е. членаan+1) и не превосх. его по модулю :|rn||an+1|
