
1 Задание
1) Если функция F(x) дифференцируема на (a;b) и F’(x)=f(x) при любом x∈(a,b), то F(x) называется первообразной для f(x).
2) Дифференцируемая на (a,b) функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F’(x)=f(x).
3)
По определению, для функции f(x),
заданной на (a,b),
совокупность всех ее первообразных
называется неопределенным интегралом
и обозначается
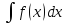 .
.
4) Неопределенным интегралом от функции f(x), непрерывной на (a,b), называется совокупность всех первообразных функции f(x).
5)
Для функции f(x),
непрерывной на (a,b),
символ
 обозначает называется совокупность
всех первообразных функцииf(x)
и, по определению, это есть неопределенный
интеграл функции f(x).
обозначает называется совокупность
всех первообразных функцииf(x)
и, по определению, это есть неопределенный
интеграл функции f(x).
6) Если функция f(x) дифференцируема на (a,b) и dF(x)=f(x)dx при любом x∈(a,b), то F(x) называется первообразной ф-ии для f(x).
7)
Если F(x)
есть первообразная для функции f(x)на
(a,b),
то совокупность F(x)+C
называется неопр. интегралом от ф-ии
f(x)
и обозначается
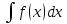 .
.
8) Если F(x) и Ф(x) – первообразные для f(x) на (a,b), то выражение (F(x)-Ф(x))’ равно 0.
9) Если F(x) и Ф(x) – первообразные для f(x) на (a,b), то их разность есть const=C.
10)
Определенным интегралом функции f(x)
на отрезке [a,b]
называется конечный предел I=limσ,
σ=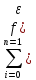 i)∆xy
xi≤
i)∆xy
xi≤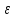 i≤xi+1
(i=0,1,…,n-1)
и обознач.
i≤xi+1
(i=0,1,…,n-1)
и обознач.
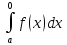 .
.
2 Задание
1)
Если А=const,
то интеграл
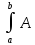 dx
равен числу A(b-a).
dx
равен числу A(b-a).
2)
Если f(x)
– интегрируема на [a,b],
то сумма
 (x)dx+
(x)dx+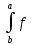 (x)dx
равна числу 0.
(x)dx
равна числу 0.
3)
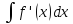 равенf(x)+C.
равенf(x)+C.
4)
По свойству определенных интегралов,
если функция f(x)
интегрируема на [a,b],
A=const,
то
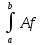 (x)dx
равен A(f’(b)-f’(a)).
(x)dx
равен A(f’(b)-f’(a)).
5)
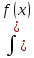 +g(x))dx
равен
+g(x))dx
равен
 +
+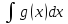 .
.
6)
По свойству определенных интегралов,
если f(x)
и g(x)
интегрируемы на [a,b],
то разность
 (x)dx-
(x)dx-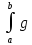 (x)dx
равна
(x)dx
равна
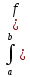 (x)-g(x))dx.
(x)-g(x))dx.
7)
Если А – число (А≠0), то
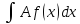 равенA
равенA .
.
8)
Выражение (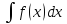 )’
равноf(x).
)’
равноf(x).
9)
Выражение
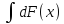 равноF’(x)+C.
равноF’(x)+C.
10)
d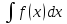 равен f(x)dx.
равен f(x)dx.
3 Задание
1)
Установить соответствие: 1.
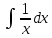 Д.ln|x|+C 2.
Д.ln|x|+C 2. xdx
Ж.
xdx
Ж.
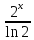 +C 3.
+C 3.
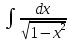 Г. –arccosx+C.
Г. –arccosx+C.
2)
Установить соответствие: 1.
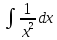 Е.
-
Е.
- +C 2.
+C 2.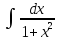 Ж.
arctgx+C 3.
Ж.
arctgx+C 3.
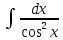 Г.
tgx+C.
Г.
tgx+C.
3)
Установить соответствие: 1.
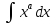 Д.
Д.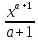 +C 2.
+C 2.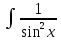 dxЗ.
-ctgx+C 3.
dxЗ.
-ctgx+C 3.
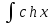 dx
В. shx+C.
dx
В. shx+C.
4)
Установить соответствие: 1.
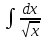 Г. 2
Г. 2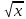 +C 2.
+C 2.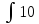 xdx
Ж.
xdx
Ж.
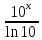 +C 3.
+C 3.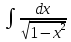 Е.
arcsinx+C.
Е.
arcsinx+C.
5)
Установить соответствие: 1.
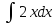 Д.
Д.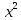 +C 2.
+C 2.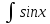 dxГ.
-cosx+C 3.
dxГ.
-cosx+C 3.
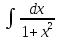 Ж.
-arcctgx+C.
Ж.
-arcctgx+C.
6)
Установить соответствие: 1.
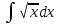 Д.
Д.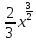 +C 2.
+C 2.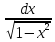 Е. -arccosx+C 3.
Е. -arccosx+C 3.
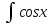 dx
В. sinx+C.
dx
В. sinx+C.
7)
Установить соответствие: 1.
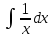 Д.
ln|x|+C 2.
Д.
ln|x|+C 2.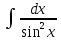 З.
-ctgx+C 3.
З.
-ctgx+C 3.
 dx
Ж.
dx
Ж.
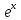 +C.
+C.
8)
Установить соответствие: 1.
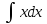 Г.
Г.
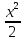 +C 2.
+C 2.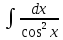 Е.
tgx+C 3.
Е.
tgx+C 3.
 dx
З.
dx
З.
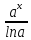 +C.
+C.
9)
Установить соответствие: 1.
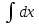 Г.x+C 2.
Г.x+C 2.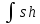 xdx
Б.
chx+C 3.
xdx
Б.
chx+C 3.
 Д.
arctgx+C.
Д.
arctgx+C.
10)
Установить соответствие: 1.
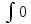 dx
Г. C 2.
dx
Г. C 2.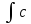 hxdx
В. shx+C 3.
hxdx
В. shx+C 3.
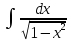 Е.arcsinx+C.
Е.arcsinx+C.
4 Задание
1)
Формулировка теоремы о замене переменной
в неопределенном интеграле такова:
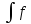 (x)dx|x=φ(u)=
(x)dx|x=φ(u)= (φ(u))·φ’(u)du
(φ(u))·φ’(u)du
2)
Если u(x)
и v(x)
– непрерывно дифференцируемые функции,
то формула интегрирования по частям
для определенного интеграла имеет вид:
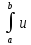 dv=uv|
dv=uv|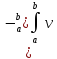 du
du
3)
Интеграл вида
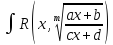 dx,
где a,b,c,d
- действительные числа, m
– натуральное число, ad-bc≠0,
R(x,y)
– рациональная функция, сводится к
интегрированию рациональной функции
заменой
dx,
где a,b,c,d
- действительные числа, m
– натуральное число, ad-bc≠0,
R(x,y)
– рациональная функция, сводится к
интегрированию рациональной функции
заменой
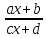 =tm,
причем dx
равен dx=
=tm,
причем dx
равен dx=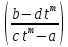 dt;
dx=
dt;
dx=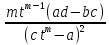 dt
dt
4)
Согласно методу подведения под знак
дифференциала для дифференцируемой
функции u=φ(x)
и интегрируемой функции g(u)
интеграл
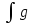 (φ(x))φ’(x)dx
равен
(φ(x))φ’(x)dx
равен
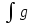 (u)du
(u)du
5)
Формулировка теоремы о замене переменной
в определенном интеграле имеет вид:
φ:[α,β]→[a,b],
∃φ’(t)
∀t∈(α,β),
φ(α)=a,
φ(β)=b,
f
непр-на на [a,b]⇒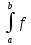 (x)dx=
(x)dx=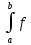 (φ(t))φ’(t)dt
(φ(t))φ’(t)dt
6)
Если u(x)
и v(x)
непрерывно дифференцируемые функции,
то формула интегрирования по частям
для неопределенного интеграла имеет
вид:
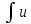 dv=uv-
dv=uv-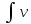 du
du
7)
Интеграл вида
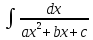 и
и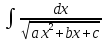 ,
гдеa,b,c
– действительные числа (a≠0)
приводятся к табличным интегралам с
помощью выделения полн. квадрата из
квадр-го 3-хчлена⇒в 2?? ax2+bx+c=a(x+
,
гдеa,b,c
– действительные числа (a≠0)
приводятся к табличным интегралам с
помощью выделения полн. квадрата из
квадр-го 3-хчлена⇒в 2?? ax2+bx+c=a(x+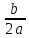 )2±k2
)2±k2
8)
Интеграл вида
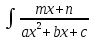 dx,
где a,b,c,m,n,
- действительные числа, (a≠0,
m≠0)
сводится к интегралу
dx,
где a,b,c,m,n,
- действительные числа, (a≠0,
m≠0)
сводится к интегралу
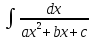 с помощью предварительно выделяя в
числителе произв. квадр-го 3-хчленаax2+bx+c
с помощью предварительно выделяя в
числителе произв. квадр-го 3-хчленаax2+bx+c
9)
Интеграл
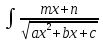 dx,
где a,b,c,m,n
– действительные числа (a≠0,
m≠0),
сводится к интегралу
dx,
где a,b,c,m,n
– действительные числа (a≠0,
m≠0),
сводится к интегралу
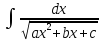 с помощью предварительно выделяя в
числителе произв. квадр-го 3-хчленаax2+bx+c
с помощью предварительно выделяя в
числителе произв. квадр-го 3-хчленаax2+bx+c
10)
Согласно методу подведения под знак
дифференциала для дифференцируемой
функции u=φ(x)
и функции g(u)
интеграл
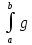 (φ(x))φ’(x)dx
равен
(φ(x))φ’(x)dx
равен
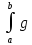 (u)du
(u)du
