Лекции Логинова [1-2 курс, МИФИ] / МАТАН 1 сем / matan_3

Лекция 8

6. Критерий Коши существования предела функции

Пусть D область определения функции f содержит проколотую окрестность т. x₀

Условие Коши: >0x,xD:|f(x)-f(x)|<

Т. (Критерий Коши) Для существования конечного предела

x₀ число или символ н. и д., чтобы f удовлетворяла условию Коши в окрестности точки x₀.

Необходимость. >0,/2 xD:|f(x)-A|</2. Для x,xD получим требуемое неравенство |f(x)-f(x)|<|f(x)-A|+|f(x)-A|/2+/2=.

Достаточность. Пусть {x_n} последовательность типа Гейне. Тогда {f(x_n)}

будет удовлетворять условию Коши для последовательностей, поэтому существует некоторый предел . Докажем, что для любой другой последовательности типа Гейне {y_n} как в Гейне предел будет также равен B. Составим последовательность

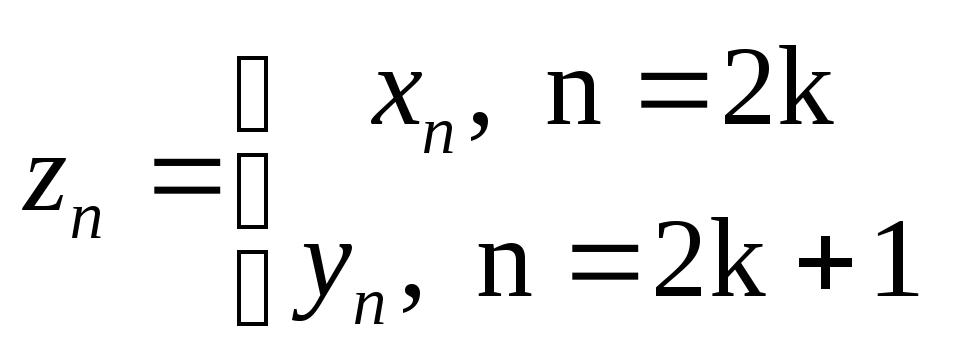
Эта последовательность будет последовательностью типа Гейне и, как уже доказано, предел должен существовать. Тогда все частичные пределы должны совпадать, в частности, =.

Сформулируем условие Коши для других случаев

Односторонние пределы: >0>0x,x(a,a+)D:|f(x)-f(x)|<

f определена в окрестности + (совпадает с обычным)

>0bx,x(b,+)D:|f(x)-f(x)|<

7. Локальная ограниченность функции, имеющей конечный предел

Область определения D функции f cодержит некоторую

f локально ограничена в точке x₀, если она ограничена в некоторой окрестности этой точки M>0xU(x₀)D:|f(x)|M.

Т. Функция f имеющая конечный предел в окрестности точки x₀ локально ограничена в точке x₀.

Доказательство: =1,M=max{|A-1|,|A+1|,f(x₀)} или M=max{|A-1|,|A+1|}

Замечание. Теорема верна и в случае

8. Сохранение знака функции, имеющей ненулевой предел в точке

Область определения X функции f cодержит некоторую

Теорема

( f(x) сохраняет знак A в некоторой окрестности точки x₀)

Замечание 1.

Замечание 2. Теорема верна и в случае

A - число или символ.

9. Предел сложной функции

f(x) определена на X, g(t) определена на T , область значений GX. Рассматривается функция F(t)=f(g(t)),tT.

Теорема. Пусть g определена на G=(,) или на (,)\{t₀},t₀ (,). f определена на (a,b) за исключением быть может точки x₀(a,b),tG:g(t)x₀, если tt₀. . Тогда

Доказательство: Пусть. Возьмем >0>0x:f(x) , далее >0t:g(t) ,tt₀g(t)x₀. таким образом,

t f[g(t)]

§3 Свойства пределов

1.Переход к пределу в неравенствах

Т1. Если f(x)g(x)h(x) определены на (a,b) за исключением быть может x₀(a,b) и , А и B числа, то AB.

Замечание. Аналогично f(x)<g(x)

Лекция 9

2. Арифметические операции над пределами

Везде в этом пункте рассматриваются конечные пределы.

1), , если .

2) , если существуют конечные пределы

3)

Следствие:

4) 

5) g(x)0,, 

Замечание: Аналогичные свойства имеют место для односторонних пределов

3.Бесконечно малые и бесконечно большие функции

Опр. Бесконечно малой в точке x₀ называется функция f(x)

такая, что

Свойства бесконечно малых функций

1) Критерий существования конечного предела

 б.м. функция при xx₀, (x):f(x)=A+(x)

2) (x),(x) б.м.  (x)+(x) б.м.

3) б.м. на ограниченную

4) Произведение б.м.

Опр. f(x) определенная в проколотой окрестности x₀ называется б.б. в т. x₀, если

5) Если (x) б.м. в т. x₀ и (x)0, то 1/(x) является б.б. и наоборот. Символически 1/=0, 1/0=

4. Сравнение б.м. и б.б. функций. Символы

f,g определенны в некоторой проколотой окрестности т. x₀

, если

Аналогично определяется при x₀x₀+0,-0,, .

Пример: f(x)=(1),x

Опр. Если при xx₀ , f(x)=(g) и g(x)=(f) , то f(x), g(x) называются функциями одного порядка

Пример: x³,x²,x1

Определение . Пусть f(x), g(x) определенны в некоторой проколотой окрестности точки x₀, пишут , если

,x:f(x)=(x)g(x)

Аналогично определяется при x₀x₀+0,-0,,

Пример: f(x)=(1),xx₀

Если , б.м. и , то говорят, что  б.м. более высокого порядка, чем .

Определение. Функции f(x), g(x) называются эквивалентными в точке x₀ ( в окрестности этой точки ), если выполнено хотя бы одно из двух условий

Замечание 1. Если выполнено одно из этих условий, то будет выполнено и второе.

Замечание 2. Эти условия можно записать в другой форме. Например, первое из них: в некоторой проколотой окрестности точки имеет место равенство f(x)=h(x)g(x),h(x)1, при xx₀.

Замечание 3. Если, например, g(x)0, то первое условие можно записать в виде .

Определение. Если f(x) эквивалентна (x-x₀)ⁿ при xx₀ , то f(x) называется бесконечно малой порядка n. Если f(x) эквивалентна 1/(x-x₀)ⁿ при xx₀ , то f(x) называется бесконечно большой порядка n.

Если f(x) б.б. при xx₀ и f(x) эквивалентна xⁿ при x , то f(x) называется бесконечно большой порядка n.

Примеры. ,,0,1,+.

При вычислении пределов полезна следующая теорема

Т2. Пусть f эквивалентна f₁,g эквивалентна g₁ при xx₀, кроме того существует конечный предел , тогда существует

Опр. Если , то g называется главной частью f при xx₀..

Лекция 10

§4 Замечательные пределы

1.

Для

см. тригонометрический круг

Т.о.

2.

5