Математические основы криптологии / VER

Теория вероятностей.

1. Алгебра событий.

Случайный или стохостический эксперимент - это идеальный эксперимент, который может быть повторен в неизменных условиях сколь угодно раз.

Пространство элементарных исходов.

₁, ₂,...,_n - элементарные исходы. {₁, ₂,...,_n}= - пространство элементарных исходов. ={Р, Г} - для монеты (решка и герб). ={1,2,3,4,5,6} - для кубика. ={Г, РГ, РРГ,...} - счетное пространство элементарных исходов (когда монету подбрасываешь до первого появления герба). Конечные и счетные пространства - дискретные постранства. =континууму - континуальное пространство элементарных исходов. Событием наз-ся А. А - выпадение четного числа: А={2,4,6}. ={четная,нечетная}, В()=А - мн-во событий. А={, ,...}. Алгеброй наз-ся любое мн-во, в котором определены две операции: сложение, умножение, причем умножение коммутативно и сущ-ет для А элемент Е_А: АЕ_А=А. Е_А=А либо Е_А=.

Пустое мн-во - не возможное событие. - событие={₁,...} - достоверное событие. А₁А₂=А₁А₂, А₁+А₂=А₁А₂, АВ - А влечет В. Если А₁А₂=, тогда А₁ и А₂ - несовместны. 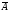- противоположное событие. 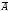={: А}, А-В=А\В. Подбрасывание 2 монет сразу: ={РР, РГ, ГР, ГГ}, _n(А)=n(А)/n - частота событий, где n - число экспериментов. Пусть на мн-ве задана р: _i р(_i):

1. i 0p(_i)1

2. p(_i)=1.

Классическое вероятностное пространство: 1) = n, ={₁, ₂,..., _n},

2. элементарные исходы равновероятны: np(_i)= p(_i)= 1 p(_i)= 1/n. - конечное мн-во; А, р(А)=р(_i) - вероятность:

1. 0р(А)1

2. р()=0, р()=1

3. р(А+В)= р(А)+ р(В)- р(АВ). Если АВ= р(А+В)= р(А)+р(В).

4. ВА: р(А-В)= р(А)- р(В), А= (А-В)В

5. р(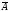)= р(-А)= р()- р(А)= 1-р(А).

Пример 1: На карточках 1,2,3,4,5. А={вторая карточка с нечетным числом}. ={(1,2), (1,3),...}, =А₅² =5*4=20. р(_i)=1/20,

А=А1+А2, где А1={первая нечетная, вторая нечетная}, А2={первая четная, вторая нечетная}. р(А)=р(А1)+р(А2), 1-ый способ: А1=6; А2=6, р(А)=6/20+6/20=3/5. 2-ой способ: А=12=n(А); n=20 р(А)=n(A)/n=12/20=3/5. Пример 2: Бросаются 2 игральные кости. А={сумма выпадений равна 7}; В={сумма равна 8}. =36, А={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)} р(А)=6/36=1/6. В={(2,6),(3,5),(4,4),(5,3),(6,2)} р(В)=5/36. (, А, р(А)) - вероятностное пространство.

Условная вероятность.

N - число людей, N_A - число работающих людей из N. N_B - число мужчин из N. Случайно выбранный человек - работающий: А={человек - работающий}; В={человек - мужчина} р(А)=N_A/N; p(A)=N_B/N, АВ={мужчина работает};

N_AB -число работающих мужчин. р(АВ)=N_AB/N. N_AB/N_B=N_AB/NN/N_B= p(AB)1/p(B). Условной вероятностью события А при условии В (р(В)0) наз-ся р(АВ)/р(В)=р(АВ), где В - гипотеза Н р(АН)=р(АН)/р(Н).

Пример 1: 3 игральные кости. На одной кости 1 при условии, что на всех 3 костях разные числа.

Н={на всех костях разные числа}; А={на одной кости 1}. Р(АН) - ?

1. Н=654=120. АН=(А1+А2+А3)Н, где А1 - на первой кости 1, А2 - на второй кости 1 и т.д. АН=А1Н+А2Н+А3Н

А1Н={на первой кости 1}, А1Н=54=20 АН=60 р(АН)=60/120=1/2

2. р(АН)=АН/=60/6³, р(Н)=120/6³ р(АН)= =60/120=1/2.

Пример 2: 10 игральных костей, при условии, что выпала хотя бы одна 1, найти вероятность, что выпало хотя бы две 1.

Н={выпала хотя бы одна 1}, А={выпало хотя бы две 1}, АН АН= А р(АН)= р(АН)/р(Н) = р(А)/р(Н)= (1-р(неА)) /(1-р(неН)), неН={ни одной единицы}, неН=5¹⁰ р(неН)=5¹⁰/6¹⁰, неА={ни одной} {выпала одна 1}; неА= 5¹⁰+105⁹ р(неА) = ( 5¹⁰+ 105⁹ )/6¹⁰ р(АН)=1-(105⁹)/(6¹⁰-5¹⁰).

Пример 3: Полицейский ищет сбежавшего вора.

С вероятностью 1/2 - в городе, С вероятностью 1/2- за городом, В городе с равной вероятностью в одном из 5 баров. Полицейский обошел 3 бара - там нет. Какова вероятность, что он найдет в 2 других барах ? Н={в 3 барах его нет}; А={в 2 других барах}; Н={либо в 2 барах}{либо за городом}. АН АН=А р(АН)= р(АН) /р(Н)= р(А)/р(Н). р(в одном баре)=1/10. р(А)=2/10=1/5. р(Н)=1-3/10=7/10 р(АН)=(1/5)/(7/10)=2/7.

Св-ва условной вероятности.

(, А, р(А))(Н, А_Н, р(АН)):

1. 0р(АН)1

2. р(А+ВН)= р((А+В)Н) /р(Н)= р(АН+ВН) /р(Н)= (р(АН)+ р(ВН)- р(АВН)) /р(Н)=р(АН)+ р(ВН)- р(АВН).

3. Если ВА, то р(А-ВН)= р((А-В)Н) /р(Н)= р(АН-ВН) /р(Н)= (р(АН)- р(ВН)) /р(Н)= р(АН)- р(ВН)

4. р(Н)=р(Н)/р(Н)=0

1. р(НН)=1

Если А и Н не пересекаются АН= р(АН)=0, Если Н влечет А, т.е. НА р(АН)=р(Н)/р(Н)=1

Независимость событий.

р(А)р(АН). Если А и Н независимы, то р(А)= р(АН)= р(АН)/р(Н). События А и Н независимы если р(АН)= р(А)р(Н).

Пример 4: Из 52 карт берут 1 карту. А={вынут туз}; В={взята пика}; С={взята дама}. А и В независимы, А и С зависимы.

р(А)=4/52=1/13; р(В)=13/52=1/4 р(АВ)=1/52. р(А)р(В)=1/131/4=1/52 А и В независимы, р(С)=1/13; р(АС)= 0 1/131/13 =169 А и С зависимы. А и В независимы неА и неВ независимы А и неВ независимы,...р(АВ)= р(А)р(В)

р(АнеВ)= р(А(-В))= р(А-АВ)= р(А)- р(АВ)= р(А)- р(А)р(В)= р(А)(1- р(В))= р(А)р(неВ).

Формула полной вероятности.

А происходит вместе с Н₁,..., Н_n: р(Н_i)0; i H_i H_j= ; AH_i . Говорят, что событие Н_i образует полную группу событий по отношению к А, тогда р(А)=р(АН_i)р(Н_i) - формула полной вероятности. Т.к. АН_i,то А=АН_i=Н_iА. Т.к. Н_i H_j= , то АН_i АН_j= р(А)= р(АН_i)= (р(АН_i)р(Н_i)) /р(Н_i)= р(АН_i)р(Н_i).

Пример: Три урны:

1. 4 белых и 3 черных

2. 2 белых и 3 черных

3. 5 белых и 1 черный

А={шар черный}, р(АН₁)=3/7; р(АН₂)= 3/5; р(АН₃)= 1/6 р(А)=1/3(3/7+ 3/5+1/6)= 151/630.

Формулы Байеса.

АН_i, где р(Н_i)0, Н_i Н_j=. р(Н_iА) - апостероирное распределение вероятности. р(Н_i) - априорные вероятности.

р(Н_iА)= р(АН_i)/р(А)= ((р(АН_i)/ р(Н_i)) р(Н_i))/ р(А)= (р(АН_i) р(Н_i))/ р(АН_к) р(Н_к), i=1,2,..., n.

Предыдущий пример: р(Н₁А)= (3/71/3)/ (151/630)= 630/1057 =90/151, р(Н₂А)= (3/51/3)/ (151/630)= 630/755= 126/151,

р(Н₃А)=135/151.

Серия независимых испытаний.

- пространство элементарных событий для одного эксперимента. _n=..., ={герб, решка} ₃= = {(ггг), (ггр), ...,(ррр)} =2³. _n= ... = ⁿ, _n= ^{(1) (2)}... ⁽ⁿ⁾. Пример: ⁽¹⁾={г, р}; ⁽²⁾={1,2,...,6} ₂= ⁽¹⁾⁽²⁾= {г1, г2,..., г6 р1, р2,..., р6}. _n - серия независимых испытаний. А_n. Пусть n=2 ₂=⁽¹⁾⁽²⁾, ⁽¹⁾={₁₁, ₁₂, ₁₃,...}, p(_1i)=p_1i : p_1i0, p_1i=1. ⁽²⁾={₂₁, ₂₂, ₂₃,...}, p(_2j)=p_2j : p_2j0, p_2j=1. ₂= {(₁₁₂₁), (₁₁₂₂), (₁₁₂₃),...}= {(_1i2j): i1,j1}, p(_1i, _2j)= p_ij= p(_1i) p(_2j), p_ij= p(_1i) p(_2j)= p_1i p_2j=1, ₃= , ₃= {(111), (112),..., (666)},

p_ijk=1/61/61/6.

Т-ма о независимости событий 1-го эксперимента с событиями 2-го эксперимента.

₂=⁽¹⁾⁽²⁾. А, В₂; А связана с ⁽¹⁾, В связана с ⁽²⁾, тогда р(АВ)=р(А)р(В), ={выпадение герба}. В={5}; А=⁽²⁾, где ⁽¹⁾, А={г1, г2, г3,...., г6}, В=⁽¹⁾, где ⁽²⁾, В={г1, р1, г2, р2,..., г5, р5}, АВ= р(АВ)= р()= р(_1i,_2j)= p_1ip_2j= p_1i p_2j= p() p(); р(А)= р(⁽²⁾)= р(_1i, _2j)= p(_1i) p(_2j)= p(). Аналогично р(В)=р() р(АВ)= р(А) р(В).

Испытания Бернулли.

Повторные испытания наз-ся испытаниями Бернулли если _n=...; ={у, н}; р(у)=р, q=р(ну)=1-р(у); =у+у+н; у - выпадение герба р=1/2; q=1/2; р()={pq p...q}; q=1-p. АУ - выпадение числа 5, р=5/6; q=1/6. b(k, n, p) вероятность k успехов из n испытаний с вероятностью успеха р. Т.о. b(k, n, p)=C_n^kp^kq^n-k. A_k, A_k={наступило k успехов}; A_k=`= =(у...н,...,у...у) p(A<sub>k</sub>)= =p(`)=p(`)=p^kq^n-k. C_n^k - k букв можно поставить на n мест. p(A_k)=C_n^kp^kq^n-k

b(0, n, p)=C_n⁰p⁰qⁿ=qⁿ, b(1, n, p)=1-b(0, n, p)=1-qⁿ - вероятность одного успеха хотя бы один. Пример: 5 выстрелов, вероятность попадания в десятку равна 1/4. р=1/4; n=5.

1. b(1, 5, ¼)=C₅¹1/4(3/4)⁴=0.4

2) b(2,5,¼)=C₅²(1/4)²(3/4)³=0.25

2. хотя бы одно 1-b(0,5,¼)=0.75

Геометрическая вероятность.

Если =континууму и А=континууму, то р(А)=(А)/(), где - мера. Примеры: 1) Попасть пулей в прутья квадратной решетки, L - расстояние между осями прутьев, а - толщина прута. Какова вероятность (La).

(А)=2а/2L+2a/2(L-a)=2aL-a², ()=L² p(A)=(2aL-a²)/L².

Случайная величина (СВ).

Х - случайная величина, наз-ся функция определенная на и принимает значения в области действительных чисел.

Х: R¹. Если область значений континуум, то говорят о непрерывности СВ. Если конечное или счетное, то СВ - дискретна (ДСВ).

ДСВ.

Область значений Х()= {Х₁, Х₂,...}; А_k= {: X()=x_k}; p(A_k)=p{X()=x_k}. Законом изменения СВ наз-ся таблица:

x x₁ x₂ x₃ ... x_n

p p₁ p₂ p₃ ... p_n p{Xx_k}=1. ДСВ хар-ся законом и функцией распределения. Функция распределения:

F_X(x)=p{X=x_k}. В каждой точке х собираются вероятности событий, при которых x_kx_i. x - число выпадаемых гербов Г.

х(){0,1,2,3}

х 0 1 2 3

р 1/8 3/8 3/8 1/8 b(1, 3, 1/8)=C₃¹p¹q², F_X(x_m+) - F_X(x_m)= p{X=x_k}- p{X=x_k}= p{X=x_m}. Если х0, то F_X(x)= p{X=x_k}= 0. Если 0х1, то F_X(x)= p{X=x_k}= p{X=0}=1/8. Если 1х2, то F_X(x)= p{X=x_k}= p{X=0}+ p{X=1}= 1/8+ 3/8= 1/2. Если 2х3, то F_X(x)= 3/8+1/8+3/8=7/8. Если х3, то F_X(x)=1.

1.Закон распределения СВ. (Биномиальное распределение СВ). Закон Бернулли.

{b(k, n, p), k=0,1,...,n} наз-ся распределением Бернулли. b(k, n, p)=C_n^kp^kq^n-k=(p+q)ⁿ=1 определяет вероятность на ={0,1,...,n}

2.Распределение Пуассона для ДСВ.

n; p0; np==const. Если n и p0 и np, то b(k, n, p)(e^-k)/k! (k=0,1,..,n). Т.к. np, то _n0 такое, что np=+_n p=(+_n)/n, b(k, n, p)=C_n^kp^k(1-p)^n-k=

Если n достаточно велико и p достаточно мало, то b(k, n, p)= (e^-k)/k!. Пример: n=500 человек; р=1/365; А - первого января родятся; =500/365=1.37; р_k=p{k человек родилось 1-го января},

p₀ p₁ p₂ p₃ p₄

254. 0.348 0.239 0.109 0.037

255. 0.348 0.239 0.109 0.037 (e^-k)/k!=e^-k/k!=e^-e=1. Набор чисел случайных величин 0,1,... с вероятностью

р_k=(e^-k)/k! наз-ся распределением Пуассона. Оно определяет набор вероятностей на ={0,1,...}. Функция от случайной величины (Х) тоже случайная величина.

Х -2 -1 0 1 2

1/5 1/5 1/5 1/5 1/5

Х² 0 1 4

1/5 2/5 2/5

Х+1 -1 0 1 2 3

1/5 1/5 1/5 1/5 1/5

Совместное распределение.

На рассмотрим Х: х₁, х₂,..., х_i

р(х₁), р(х₂),..., р(х_i) и Y: y₁, y₂,..., y_i

p(y₁), p(y₂),..., p(y_i). A_ij={: X()=x_i, Y()=y_j}, тогда набор р(x_i, y_j)=р(А_ij) будет наз-ся совместным распределением СВ X и Y. Пример 1: х - число гербов, y - число решек при одном бросании.

х 0 1 2 y 0 1

р 1/4 1/2 1/4 р 1/2 1/2

Y\X 0 1 2 (гербы)

0 0 ¼ ¼

1 ¼ ¼ 0

(решки)

Св-ва совместного распределения:

1. р(x_i, y_j)0 i, j

2. A_ij - полная группа событий. р(А_ij)= p(x_i, y_j)=1

3. i p(x_i, y_j)= p(x_i), j p(x_i, y_j)= p(y_j). p(x_i,y_j)= p{(X=x_i) (Y=y_j)}= p{(X=x_i) (Y=y_j)}= p{(X=x_i) (Y=y_j)}= p{(X=x_i) }= p(x_i).

СВ X и Y наз-ся независимыми если явл-ся независимыми события {X=x_i} и {Y=y_j} при i,j. p{(X=x_i) (Y=y_j)}= p{X=x_i} p{Y=y_j}= p(x_i) p(y_j), т.е. p(x_i, y_j)=p(x_i)p(y_j). Если СВ Х_k связана только с k-ым испытанием, то X₁, X₂,... будут независимыми. Пример 2: Кость бросается 4 раза. X - CB={сумма очков при 2-х первых бросаниях}; Y - СВ={максимум очков при остальных 2-х бросаниях};

Х 2 3 4 5 6 7

р 1/36 2/36 3/36 4/36 5/36 6/36

Х 8 9 10 11 12

р 5/36 4/36 3/36 2/36 1/36

Y 1 2 3 4 5 6

р 1/36 3/36 5/36 7/36 9/36 11/36

p(x_i, y_j)=p(x_i)p(y_j)

Условным распределением СВ наз-ся вероятность p(X=x_iY=y_j)= p((X=x_i) (Y=y_j))/ p(Y=y_j)= p(x_i, y_j)/ p(y_j)

p(X=0Y=0)=0

p(X=1Y=0)=(1/4)/(1/2)=1/2

p(X=2Y=0)=(1/4)/(1/2)=1/2

МО - матожидание;

МХ - матожидание СВ Х.

n - семей; n_k - число семей, в которых к-детей. n=n₀+n₁+n₂+... . m=0n₀+1n₁+2n₃+3n₃+... - общее число детей. m/n= 0n₀/n+1n₁/n+2n₂/n+3n₃/n+.. . X - число детей в случайно выбранной семье.

Х 0 1 2 3 ....

р n₀/n n₁/n n₂/n n₃/n.... . MX=x_ip(x_i)=m/n - среднее значение случайной величины. Если данный ряд сходится абсолютно, то говорят, что величина имеет матожидание. Пример 1: СВ Х распределена по биномиальному закону, тогда

Х 0 1 ... k n

p b(0,n,p)...b(k,n,p)=C_n^kp^kq^n-k

MX= kC_n^k p^k q^n-k= pk C_n^k p^k-1 q^n-k= p(C_n^k p^k q^n-k)`<sub>p</sub>= p(C<sub>n</sub><sup>k</sup> p<sup>k</sup> q<sup>n-k</sup>)`_p= p[(p+q)ⁿ]`_p= pn(p+ q)^n-1=np. Пример 2: СВ Х распределена по закону Пуассона.

X 0 1 .... k n

p e^- e^- .... (e^-k)/k!

MX= k(e^{- k})/k!= e^-(k ^k)/k!= e^-(k ^k-1)/k!= e^-(^k/ k!)`= e<sup>-</sup>(<sup>k</sup>/ k!)`= e^- (e)`=. ДХ - дисперсия СВ Х - наз-ся её среднее отклонение от её среднего значения. ДХ=М(Х-МХ)²=(Х_k-MX)²p(x_k). Пример 1: СВ Х распределена по закону Бернулли. Хb(k, n, p), Y_i={1,если в i-ом испытании успех - р; 0, если в i-ом испытании неудача - 1-р}, X=S_n - число успехов в n испытаниях. S_n=Y₁+Y₂+...+Y_n, ДХ= ДS_n= ДY_i

Y_i 0 1

p 1-p

ДY_i= M(Y_i²) - (MY_i)²= p-p², ДX= np(1-p)= npq, Пример 2: Х распределена по закону Пуассона.

X 0 1 2 ...

p e^- e^- (²e^-)/2 ...

ДХ= MX²- (MX)², MX²= k² e^{- k}/k!= e^-(k^{2 k})/k!= ²e^-(k^{2 k-2})/ k!= ²e^- [(^k/ k!)``+ (k<sup>k-2</sup>)/k!]= <sup>2</sup>e<sup>-</sup> (<sup>k</sup>/ k!)``+ e^- (k^k)/ k!= ²+, ДХ= ²+-²=.

Св- ва матожидания.

1. МС=С (С=const), 2. M(X)=MX (=const), 3. M((X))=(x_k)p(x_k).

• (X)=Y

Y y₁ y₂ y₃ ....

p p(y₁) p(y₂) p(y₃) ....

M((X))= MY= y_i p(y_i)= y_i p((x_k)=y_i)= (x_k) p(x_k)= (x_k) p(x_k).

4. M(X+Y)= MX+MY.

• M(X+Y)= (x_i+y_j) p(x_i, y_j)= x_i p(x_i, y_j)+ y_j p(x_i, y_j)= x_i p(x_i, y_j)+ y_j p(x_i, y_j)= x_ip(x_i)+ y_jp(y_j)= MX+MY.

5. X и Y - независимы, то M(XY)= M(X)M(Y)

• M(XY)= x_iy_jp(x_i, y_j)= x_iy_j p(x_i) p(y_j)= x_ip(x_i) y_jp(y_j)= MXMY.

Cв-ва дисперсии.

1. ДC=0

2. Д(aX+b)= a²ДХ

• Д(aX+b)= M(aX+ b- M(aX+b))²= M(aX+ b-aMX- b)²= a²M(X- MX)²= a²ДХ.

3. ДX= M(X-MX)²= M(X²- 2XMX+ (MX)²)= M(X²)- 2(MX)²+ (MX)²= M(X²)- (MX)²

4. Если Х₁, X₂,....,X_n независимые СВ, то Д(X₁+...+X_n)= ДХ₁+....+ДХ_n. Д(X+Y)=ДX+ДY, Д(X+Y)=M(X+Y-M(X+Y))²= M(X+Y- MX- MY)²= M((X- MX)+ (Y- MY))²= M[(X- MX)²+ (Y- MY)²+ 2(X- MX)(Y- MY)]= ДХ+ДY+ 2M(X- MX) (Y-MY)= ДХ+ ДY+ 2M(X- MX)M(Y- MY)= MX- MX=0; MY- MY=0= ДХ+ДY.

Непрерывная СВ.

F_X(x)=p(Xx) xR¹, p(Xx)=p(X=x_i).

Cв-ва:

1. 0F_X(x)1

2. F_X(x) не убывающая x₁x₂ p(Xx)=p{: X()x}.

3. F_X(x) непрерывна слева lim F_X(x)= F_X(x₀-) (при xx₀) f_X(x) - плотность распределения СВ. F_X(x)= (от - до х )f_X(t)dt

MX= (от - до + )xf_X(x)dx; ДХ= (от - до + )(X-MX )²f_X(x)dx

Cв-ва плотности:

1. f_X(x)0, F_X`(x)=f_X(x) в точке где f_X(x) непрерывна.

2. (от - до +) f_X(x)dx=1, X=ДХ - среднее квадратичное отклонение. Если МХ=0,то Х-центрированная. Если МХ=0 и Х=1, то Х - стандартизованная. Вероятность попадания в интервал: x₁X x₂. p{:X( ) x₁ X() x₂}=p{:X( ) x₂}-{:X()x₁}= p{:X() x₂}- p{:X() x₁}= F_X(x₂)- F_X(x₁)= (от - до x₂ )f_X(x)dx- (от - до x₁ )f_X(x)dx= (от х₁ до х₂)f_X( x)dx.

Пример 1: Х описывается по показательному закону

f_X(x)=0, если х0, f_X(x)= e^-, если х0, МХ - среднее время безотказной работы аппаратуры, МХ= (от - до + )хf_X(x)dx= (1/ )(от 0 до )xe^-Xdx= (1/) (от 0 до )te^-tdt= (1/)( te^-tот 0 до - (от 0 до )e^-tdt)= 1/, ДХ= (от - до + )(X-MX )²f_X(x )dx= (от 0 до )(X²- 2X/+ 1/² )e^-Xdx= -(от 0 до )Xe^-Xdx- 2(от 0 до )Xe^-Xdx+ (1/²)(от 0 до )e^-Xdx= 1/²

Пример 2: р{радиоаппаратура не выйдет из строя за время t=MX}. X - время безотказной работы. P(XMX)= 1-p(XMX)=1-F_X(MX)= 1 - (от - до МХ )f_X(MX)dx= 1 - (от 0 до 1/ )e^-Xdx= 1+e^-Xот 0 до 1/= 1/e.

Т-ма Чебышева.

Если ДХ сущ-ет (интеграл сходится абсолютно), тогда (0) p{X-MX} ДХ/². p{X-MX}= p{: X()-MX }= p(x_k) (X_k-MX)²/ (X-MX)² (1/²)(X_k- MX)²p(x_k) (1/² )(X_k- MX)²p(x_k)= ДХ/².

Закон больших чисел.

Если S_n - число успехов в серии из n испытаний, то S_n/n - частота успеха. При n S_n/np. Закон больших чисел:

Пусть y₁,..., y_n - независимые СВ с одинаковыми My_i=n и Дy_i=², тогда p{(y₁+...+y_n)/ n - }0 (при n).

• (y₁+...+ y_n)/n – СВ, M((y₁+...+ y_n)/ n)= ((y₁ +...+ y_n)/ n)= (1/n)(y₁ +...+y_n)= (1/n)n=. Д((y ₁+...+ y_n)/n)= (1/n² )(y₁+ ... +y_n)= (1/n²) n²= ²/n, p{(y₁+ ... +y_n)/ n - } ²/(n²) 0 (при n). Пример: y_i - успех в i-ом испытании.

y_i 0 1

p 1-p p p{S_n/n - }= p{(y₁+ ... +y_n)/n - p } p(1-p)/ (n²)1/(4n²).