Лекции по криптологии / Y12_M01_L07

Лекция 7. Подстановки.

7.1.Группа подстановок..

Подстановкой называется взаимнооднозначное отображение конечного множества на себя. Обычно подстановки записывают в виде двух строк.

Верхняя строка является операндом подстановки, а нижняя - результатом ее действия на операнд.

Например, одна из подстановок, действующих на множестве из пяти элементов может быть записана следующим образом: .

Элементы конечного множества всегда можно перенумеровать, следовательно и операнд любой подстановки можно записать в виде 1,2...n, где n - количество элементов в операнде. Число n называется степенью подстановки. Указанная подстановка Т является, таким образом, подстановкой пятой степени и может быть записана так: .

Очевидно, различными подстановками одной степени можно воздействовать на исходное множество последовательно друг за другом.

Результат последовательного действия подстановок называется их произведением и записывается обычно .

Произведение двух подстановок определяется исходя из того, что если первая подстановка переводит j на место i, а вторая подстановка, переводит k на место j, то в произведении k переходит на место i. Таким образом, если, ,,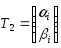 то , например, при и , .

Легко видеть, что , т.е. произведение подстановок некоммутативно, однако скобки в произведениях можно расставлять произвольно. Существует «единичная» подстановка I, такая, что для всех T : IT=TI=T. Для нашего примера .

Также нетрудно видеть, что для любой подстановки существует обратная подстановка , такая, что . Действительно, для построения достаточно переставить местами строки в подстановке , а затем упорядочить колонки так, чтобы числа в верхней строке шли в возрастающем порядке.

Перечисленных свойств вполне достаточно, чтобы классифицировать множество подстановок степени n, с указанной операцией умножения, как группу. Эта группа обозначается и называется симметрической группой -ой степени.

Заметим также, что в некотором смысле, подстановки степени n могут быть сконструированы из подстановок меньшей степени.

Дело в том, что подстановки степени nN могут действовать на операнде из N элементов, если считать, что каждый из N-n дополнительных элементов не перемещаются (переходят в себя). Например, при дополнении каждого операнда элементами n+1, n+2 ... N, можно считать, что =.

Исходя из этого, можно говорить о том, что подстановки меньшей степени включаются во множество подстановок большей степени и, в свою очередь, образуют теперь уже подгруппу по исходной операции умножения.

7.2. Циклы и транспозиции. Подобные подстановки.

Оказывается, каждую подстановку Т можно представить в виде произведения T= некоторых специальных подстановок, называемых циклами, причем, циклы попарно независимы. Последнее означает, что подстановки и , при , действуют на непересекающихся подмножествах операнда подстановки Т, если не принимать во внимание элементы, остающиеся неподвижными. Поясним указанное свойство подстановок более конкретно.

Пусть 1kn и Р - подстановка степени n, причем РI. Подстановка Р называется k-членным циклом, если она не перемещает N-k элементов, а ее действие на оставшиеся k элементов: можно представить в в виде циклической диаграммы переходов: . В этой диаграмме допускается только один переход от элемента с большим индексом, к элементу с меньшим индексом, а именно: .

Например, трехчленный цикл пятой степени может выглядеть следующим образом: . Здесь элементы 4 и 5 неподвижны, причем , , .

Ясно, что циклическая диаграмма переходов, может быть выписана, начиная с любого своего элемента, однако все эти записи соответствуют одной и той же подстановке. Обычно цикл записывают в виде, аналогичном диаграмме переходов: , а единичную подстановку рассматривают как произведение одночленных циклов вида , где под i подразумевается любой элемент (от 1 до n).

Для записи подстановки в виде произведения циклов достаточно выписать все различные диаграммы переходов. Например, подстановка может быть представлена как , впрочем, одночленные циклы при записи часто опускаются.

Запись подстановки в виде произведения циклов называется циклической записью.

Наиболее простым циклом, очевидно, является подстановка, которая переставляет местами только два элемента. Такой двучленный цикл называется транспозицией. Оказывается, можно показать, что если подстановка степени N разлагается в произведение r попарно независимых циклов (включая и одночленные циклы) то ее можно представить в виде произведения n-r транспозиций. Заметим, что в этом представлении транспозиции не обязательно являются независимыми циклами.

Величина называется декрементом подстановки.

Определение. Подстановка называется регулярной, если ее циклическая запись состоит из циклов равной длины.

Определение. Подстановка называется полноцикловой, если ее цикловая запись состоит из одного цикла.

7.2.1. Корни из подстановок.

Определение. Степенью произвольной подстановки называется -кратное произведение подстановки саму на себя.

Для записи в цикловом виде достаточно каждый цикл подстановки преобразовать следующим образом.

Пусть , . Выбираем элементы с шагом , начиная с любого скажем, первого, элемента текущего цикла. Записываем их последовательно. При первом повторении среди выбранных элементов закрываем результирующий цикл. Если символы исходного цикла не исчерпаны, выбираем один из элементов, не входящих в результирующий цикл и действуем аналогично. После выбора всех элементов цикла, переходим к следующему циклю исходной подстановки.

Примечание. Выбор элементов с шагом , означает выбор элементов с номерами , и т.д., где - длина соответствующего цикла.

Пример. Начинаем с первого элемента первого цикла подстановки , записываем: . Затем выбираем элемент с номером , т.е. через один от исходного и дописываем его в формируемый цикл: .

Выбираем элемент с номером , т.е. через один от текущего, но в цикл его не дописываем, т.к. этот элемент уже находится в формируемом цикле. Выбираем в первом цикле подстановки элемент, не принадлежащий циклу , например, и открываем новый цикл: . Затем выбираем элементы с шагом , начиная с элемента : . Поскольку сформированные циклы содержат все элементы исходного цикла, то его преобразование закончено. Итак, .

Следующие циклы дают , . В итоге, .

Задача нахождения , исходя из , не однозначна. Действительно, элементы цикла в цикловой записи исходной подстановки могли находиться в любом месте и быть к тому же циклически сдвинуты (циклы равны, с точностью до циклического сдвига). Единственное, что известно, это расстояние между элементами, т.е. они были расположены в исходной подстановке как , либо . Элементы второго цикла должны быть расположены аналогично: , либо . Совместно они могут располагаться различными способами, например: . Для нахождения корней степени из подстановок необходимо учитывать все варианты возможного взаимного расположения элементов циклов, которое зависит от , и длин циклов исходной подстановки.

7.2.2. Подобные подстановки

Подстановки одной степени называются подобными, если существует подстановка , такая, что .

Уравнение относительно называется уравнением подобия.

Определение. Цикловой структурой подстановки называется запись вида , где - количество различных длин циклов в циклической записи подстановки, длина одного из ее циклов, а - количество циклов длины, входящих в подстановку.

Теорема. Подстановки подобны в том и только том случае, когда их цикловые структуры одинаковы.

Решение уравнения подобия состоит в следующем.

1. Записываем в цикловой форме.

2. Если цикловые структуры не совпадают, то решений нет.

3. Подписываем цикловые записи подстановок друг под другом таким образом, чтобы под каждым циклом оказался цикл равной длины, причем в верхней строке записываем циклическую запись подстановки .

4. В каждой группе циклов одинаковой длины, в одной из строк, скажем нижней, произвольно переставляем циклы местами. При каждой конфигурации расположения циклов, каждый цикл независимо от других выписываем с каждого места. Преобразование производим с каждой группой циклов независимо.

Любая из множества полученных двухстрочных записей (подстановок) является решением уравнения подобия.

7.3. Декремент и четность подстановки. Детерминант матрицы.

Определение. Подстановка называется четной (нечетной) если ее декремент четен (нечетен) соответственно.

Знаком (характером) подстановки называется значение .

Ранее мы рассматривали детерминанты матриц над полями характеристики два.

В общем случае определитель матрицы порядка над полем выражается как знакопеременная сумма всех членов определителя, соответствующих подстановкам группы : .