rol_nauki_v_razvitii_obshchestva_sbornik_statey_mezhdunarodn

УДК 67

А.А. Терпяков, аспирант II года Московский государственный университет им. М. В. Ломоносова Механико-математический факультет Кафедра вычислительной механики

МОДЕЛИРОВАНИЕ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК ТЕКСТИЛЬНЫХ КОМПОЗИТОВ

Введение.

Актуальность темы исследования определяется использованием текстильных композитов различных конфигураций в строительстве, машиностроении, авиакосмической, нефтегазовой и других отраслях. В связи с широким использованием данного класса материалов, возникла необходимость проводить механическое моделирование новых материалов.

Текстильным композитом называют материал, основой которого являются жесткие нити, уложенные переплетающимися слоями и залитые «матрицей» из эпоксидной смолы, металла или керамики. Также иногда добавляется нить, прошивающая все слои материала.

Рисунок 1. Пример ортогонального композита.

Текстильные или тканые композиты представляют собой армирующий тканый материал, находящийся в матрице, позволяющую армированию удерживать форму. Как правило, армирующий материал может быть выполнен в одной из трёх форм

[2]:

частицы с приблизительно равными измерениями;

волокна (нити);

разорванные нити.

Будем рассматривать композиты, в которых армирующим материалом являются длинные волокна, возможно, с дефектами в виде полного или частичного разрыва нити. Композиты принято разделять на три типа по виду матрицы [2]:

композиты с металлической матрицей;

композиты с керамической матрицей;

композиты с полимерной матрицей.

71

Наибольший интерес для моделирования и изучения с точки зрения промышленности на данный момент представляют композиты с полимерной матрицей. Композитами с полимерной матрицей называются материалы, в которых армирующие волокна вставлены в какой-либо пластик: эпоксидную смолу, полиэстер, полипропилен. Волокна обычно формируются из стекла, углерода (графита) или арамида (кевлара) и могут принимать любую форму: тканые волокна, ненаправленные нити, узлы.

Имеет смысл моделировать тканые композиты эффективным материалом [1-3] с осредненными по пространству механическими свойствами — эффективными свойствами [4, 5].

Эффективным материалом мы назовём однородный материал, удовлетворяющий условию: если этим материалом заполнить представительный объём, то средние напряжения по объёму в исходном и эффективном материале будут равны при одинаковых перемещениях граней.

Особенности вычисления эффективных свойств тканого композита состоят в том, что он является анизотропным армированным материалом, а модули упругости матрицы и армирующих волокон могут различаться на 3-4 порядка.

Вывод расчетных формул.

Для решения поставленных задач использовались соотношения теории упругости при малых деформациях, примененные к изотропным и ортотропным материалам.

0

R, R – радиус-вектор частицы в начальном и текущем состояниях;

0	– вектор перемещений;
u R R			1
Тензор деформаций Грина при малых деформациях:		0		0	0
		E		( u u )
			2

Закон Гука:

Уравнение движения: 0

Рассматриваются периодические ячейки нескольких типов [6, 7]: 1. ячейка 2х2 волокна, переплетенная по диагонали

72

2. ячейка ламинарного композита размером 2х2 волокна

3. ортогональная ячейка с прошивающей нитью

Для представительного объёма V0, выделенного в начальном состоянии (до деформации) решаем определённое количество последовательностей краевых задач теории упругости:

0		(1)
с граничными условиями
u	uГ
	0	(2)

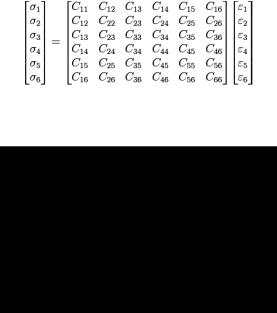
Материалы матрицы и армирующих нитей описываются законом Гука для ортотропных материалов:

Также для ортотропного материала связь напряжений и деформаций может быть записана в следующем виде:

73

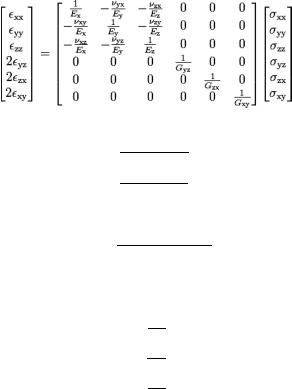
Выразим параметры материалов через коэффициенты Cijkl :	, тогда
Пусть

Каждая последовательность решаемых задач соответствует определённому виду

0

тензора деформаций Грина E e эффективного материала. В свою очередь, разные задачи в рамках одной последовательности различаются величиной деформации. Могут быть решены следующие последовательности задач:

1)11 q – растяжение или сжатие по оси X,

2)22 q – растяжение или сжатие по оси Y,

3)33 q – растяжение или сжатие по оси Z,

4)12 q – сдвиг в плоскости XY,

5)13 q – сдвиг в плоскости XZ,

6)23 q – сдвиг в плоскости YZ,

где q – величина деформации.

Решая каждую из задач каждой последовательности, находим тензор напряжений σ. Зная его, вычисляем тензор напряжений σe эффективного материала по следующей формуле:

	e	1	dV	1	N Rd	(4)
		V		V
			V

Последнее равенство в (4) получено с использованием формулы ГауссаОстроградского и того, что

74

( R) ( )R ( R) ( )R I

(5)

Зная компоненты перемещений и тензор истинных напряжений, мы можем вычислить тензор деформаций Грина эффективного материала:

0	1	0	0	(6)
E		( u u )
	2

Эффективные определяющие соотношения будем искать в виде зависимости тензора напряжений от тензора Грина E :

0	(0)	0	(7)
ije C ijkl Ekle

На практике удобнее задавать не аффинор деформаций эффективного материала, а тензор деформаций Грина – и, зная его, вычислять аффинор из формулы (6). Поскольку аффинор – несимметричный тензор второго ранга, определить его однозначно из симметричного тензора Грина не получится. Поэтому мы задаём его верхнетреугольным – тогда шесть его компонент однозначно определяются по шести независимым компонентам тензора Грина.

Вычислив аффинор, мы прикладываем к модели граничные условия (2), решаем краевую задачу теории упругости и находим σ. С помощью осреднения по формуле

(4) вычисляем эффективный тензор напряжений σe, далее из (7) находим тензор напряжений . Затем для каждой последовательности задач строится зависимость компонент тензора напряжений от величины деформации q. Эти зависимости аппроксимируются выражениями вида:

0	(8)
ije ij q

Коэффициенты αij могут быть определены, к примеру, с использованием метода наименьших квадратов. Коэффициенты Cijkl из (7) определяются через коэффициенты αij, вычисленные для соответствующей последовательности задач:

		q		0	0
1)	0
	E e 0 0 0					ije	Cij11q
			0	0	0
		0		0	0
2)	0
	E e 0 q 0					ije	Cij 22q
			0	0	0
		0		0	0
3)	0
	E e 0 0 0					ije	Cij33q
			0	0	q
		0		q	0
4)	0						Cij12 Cij21 q
	E e q 0 0					ije
			0	0	0
		0		0	q
5)	0						Cij13 Cij31 q
	E e 0 0 0					ije
				0	0
		q
		0		0	0
	0
6)	E e 0 0 q					ije Cij 23 Cij32 q
			0	q	0

Будем считать Cijkl = Cijlk.

75

Расчеты.

Численные расчеты осуществлялись методом конечных элементов с использованием системы инженерного прочностного анализа ANSYS [8-12].

Для проверки работы программы на ANSYS была использована следующая модельная задача: для ячейки размером 2х2 нити (модель 2) была построена конечно-элементная сетка, затем каждому элементу были заданы упругие

константы соответствующие стали (E = 1 ГПа,				v = 0.3). Затем проводился расчёт
эффективных свойств Cijkl и вычисление на				их основе ортотропных свойств
материала			и их сравнение с исходными данными.
Результаты расчёта представлены в таблице 1.
	Таблица 1. Проверка достоверности результатов программы.
	Коэффициент	Исходное значение,	Результат расчёта,		Погрешность,
		ГПа		ГПа	%
		2.1	2.100227968		0.010855619
		2.1	2.099617961		0.018192333
		2.1	2.101317939		0.062759
		0.3	0.300018173		0.006057794
		0.3	0.299994774		0.001741909
		0.3	0.299988274		0.00390858
		8.08	8.076924848		0.038058812
		8.08	8.076924848		0.038058812
		8.08	8.076924848		0.038058812

Результаты численного решения сравнивались с исходными значениями модуля Юнга, коэффициента Пуассона и аналитически вычисленными значениями модуля сдвига. Таким образом, можно отметить высокую достоверность используемого программного модуля для расчёта эффективных свойств. Кроме этого, достоверность полученных результатов подтверждается постановкой задачи механики деформируемого твёрдого тела, соблюдением условий симметрии, сходимостью результатов при измельчении сетки.

В современной промышленности используется множество композитных материалов, которые можно разделить на две непересекающиеся группы: материалы с изгибом армирующих волокон и материалы без изгиба армирующих волокон – рисунок 2, 3 соответственно.

Рисунок 2. Схема однослойного композитного материала с изгибом армирующих волокон.

76

Рисунок 3. Схема однослойного композитного материала без изгиба армирующих волокон (ламинарного).

Очевидно, что механические свойства композитных материалов с переплетением армирующих нитей будут отличаться от механических свойств ламинарных композитов. Были рассмотрены две периодические ячейки 2х2 волокна с изогнутой и плоской формой армирующих нитей.

Были рассмотрены два материала, используемые для изготовления армирующих нитей: кевлар и углеродные волокна. Механические свойства нитей и эпоксидной матрицы представлены в таблицах 2, 3 и 4.

Таблица 2. Механические свойства кевларовых волокон

, МПа	104 000
	5 400
	5 400
	0.4
	0.4
	0.4
	12 000
	12 000
, МПа	12 000

Таблица 3. Механические свойства углеродных волокон

, МПа	230 000
	15 000
	15 000
	0.3
	0.3
	0.3
	50 000
	50 000
, МПа	50 000

Таблица 4. Механические свойства эпоксидной матрицы

E, МПа	3 000
	0.3

77

Рассчитанные эффективные свойства представлены в таблицах 5-8.

Таблица 5. Механические свойства композита с переплетенными кевларовыми нитями

, МПа	1 462
	1 455
	4 195
	0.3732
	0.2967
	0.3018
	2 754
	2 980
, МПа	5 872

Таблица 6. Механические свойства ламинарного композита с кевларовыми нитями

, МПа	1 396
	1 373
	4 228
	0.3651
	0.3094
	0.3112
	2 991
	3 465
, МПа	6 162

Таблица 7. Механические свойства композита с переплетенными углеродными нитями.

, МПа	1 471
	1 460
	6 732
	0.3918
	0.2873
	0.3061
	3 385
	6 323
, МПа	1 648

Таблица 8. Механические свойства ламинарного композита с углеродными нитями.

, МПа	1 396
	1 373
	4 228
	0.3651
	0.3094

78

	0.3112
	2 991
	3 465
, МПа	6 162

Из приведенных в таблицах 5-8 данных можно сделать вывод, что переплетение волокон положительно влияет на прочностные характеристики композитного материала. Для композитных материалов с кевларовыми армирующими нитями переплетение увеличивает модуль Юнга на 5%, а в случае с углеродными волокнами

—на 7%.

Взадаче рассматривается периодическая ячейка тканого композита с переплетенными армирующими нитями. Были смоделированы два типа дефектов нити: трещина (зона дефекта ничем не заполнена) и дефект нити при производстве (зона дефекта заполнена материалом матрицы). Механические параметры материалов нитей и матрицы представлены в таблицах 2 и 4. Ниже представлены результаты расчётов эффективных свойств тканых композитов с дефектами при различных размерах зоны образования дефекта (размер 0.0 соответствует материалу без дефекта).

Таблица 9. Случай частичного обрыва нити с заполнением дефекта матрицей.

Размер
зоны	0.0	0.05	0.1	0.15	0.2
образован
ия дефекта
, МПа	1462,54	1468,023	1471,551	1474,655	1482,316
	1455,087	1459,634	1467,04	1469,451	1475,874
	4195,085	4190,554	4187,674	4185,03	4181,257
	0,3732	0,3732	0,3733	0,3733	0,3727
	0,2967	0,2966	0,2964	0,2966	0,2967
	0,3019	0,3018	0,3019	0,3018	0,3017
	2754,087	2750,252	2747,326	2745,906	2742,79
	2980,049	2976,705	2974,892	2972,66	2968,128
, МПа	5872,504	5858,157	5842,161	5836,527	5821,325

Таблица 10. Случай частичного обрыва двух нитей с заполнением дефекта матрицей.

Размер
зоны	0.0	0.05	0.1	0.15	0.2
образован
ия дефекта
, МПа	1462,54	1475,587	1486,351	1490,372	1496,929
	1455,087	1467,257	1478,302	1482,99	1493,188
	4195,085	4184,932	4177,415	4173,425	4168,356
	0,3732	0,3731	0,3722	0,3726	0,3731
	0,2967	0,2965	0,2964	0,2964	0,2967
	0,3019	0,3017	0,3019	0,3020	0,3015

79

	2754,087	2744,508	2738,111	2734,846	2732,232
	2980,049	2968,055	2963,63	2965,464	2966,963
, МПа	5872,504	5838,098	5808,639	5796,884	5772,434

Таблица 11.Случай частичного обрыва нити без заполнения дефекта матрицей.

Размер
зоны	0.0	0.05	0.1	0.15	0.2
образован
ия дефекта
, МПа	1462,54	1462,536	1462,387	1462,489	1462,167
	1455,087	1454,874	1454,883	1454,565	1454,653
	4195,085	4184,311	4177,935	4168,849	4160,934
	0,3732	0,3731	0,3730	0,3728	0,3728
	0,2967	0,2963	0,2966	0,2959	0,2967
	0,3019	0,3022	0,3021	0,3028	0,3020
	2754,087	2748,751	2746,682	2743,442	2740,198
	2980,049	2971,719	2973,282	2974,054	2973,22
, МПа	5872,504	5853,221	5845,752	5820,561	5811,25

Таблица 12. Случай частичного обрыва двух нитей без заполнения дефекта матрицей.

Размер
зоны	0.0	0.05	0.1	0.15	0.2
образован
ия дефекта
, МПа	1462,54	1462,338	1462,1	1462,157	1461,632
	1455,087	1454,749	1454,566	1454,259	1454,189
	4195,085	4171,018	4156,167	4142,294	4127,238
	0,3732	0,3729	0,3728	0,3724	0,3724
	0,2967	0,2966	0,2967	0,2966	0,2975
	0,3019	0,3021	0,3020	0,3029	0,3022
	2754,087	2742,576	2736,502	2732,002	2727,466
	2980,049	2971,425	2964,367	2959,981	2956,293
, МПа	5872,504	5828,967	5809,322	5782,404	5755,395

Таблица 13. Случай полного обрыва нити с заполнением дефекта матрицей.

Размер
зоны	0.0	0.05	0.1	0.15	0.2
образован
ия дефекта
, МПа	1462,54	1488,757	1507,065	1524,652	1546,877
	1455,087	1486,571	1507,508	1529,19	1550,329
	4195,085	4165,99	4145,704	4127,393	4108,271
	0,3732	0,3725	0,3718	0,3700	0,3687
	0,2967	0,2964	0,2969	0,2977	0,2991

80