8. Дисперсия альтернативного признака.

Среди варьирующих признаков, которые изучает статистика, встречаются признаки вариации, которые проявляются в том, что у одних единиц совокупности они встречаются, у других нет.

Признаки, которыми обладают данные единицы и не обладают другие, называются альтернативными.

Количественно вариация альтернативного признака в численности всей совокупности обозначается а доля единиц, не обладающих признаком, обозначаетсяи принимает значения, тогда:

Среднее значение альтернативного признака равно доле, которая является обобщающей характеристикой совокупности по этому варьирующему признаку:

Тогда дисперсия альтернативного признака равна:

Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Т.к., , то средний квадрат отклонений не может быть больше 0,25.

9. Приемы анализа вариационных рядов.

Закономерные изменения частот за счет изменения варьирующего признака в вариационных рядах называется закономерностями распределения.

Главной задачей анализа вариационных рядов является выявление закономерностей распределения и характера распределения.

Например, распределение рабочих по уровню заработной платы зависит от условий:

• квалификации;

• нормы выработки;

• расценок;

• условий труда – это общее условие.

Тип закономерности распределения – это отражение в вариационных рядах общих условий, определяющих распределение в однородной совокупности. Общие условия, определяющие тип закономерностей, познаются анализом сущности явления тех его свойств и условий, которые определяют изменчивость вариационного признака. Следовательно, должна быть построена кривая распределения. Кривая распределения – это графическое изображение частот варьирующего ряда в виде непрерывной линии, где частоты связаны с вариантами функционально. Существует теоретическая кривая распределения и фактическая.

Теоретическая кривая выражает общую закономерность данного распределения в чистом виде исключающую влияния случайных условий.

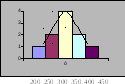
Рис. 4. Полигон распределения

Полигон распределения – непрерывная линия, характеризующая фактическую кривую распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.

В статистике наиболее часто для сопоставления фактических и теоретических кривых используют нормальный тип распределения, который имеет следующее уравнение:

где - ордината кривой нормального распределения /частость/,- это нормированное распределение.

В экономической статистике кривая нормального распределения (рис. 5) встречается достаточно редко, но нормальное распределение может служить моделью для выяснения степени и характера отклонения от нее фактического распределения.

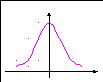
Рис. 5. Кривая нормального распределения

Выравнивание фактического распределения по кривой нормального распределения.

Cостоит из нескольких этапов:

• сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения;

• проверяют на сколько распределение признака соответствует нормальному.

					Теоретическая частота	Комулятивная частота
						фактич.	теоретич.
195	2	45,2	2,469	0,01888	1,2895	2	1,3	0,7
205	5	35,2	1,240	0,06316	4,3138	7	5,6	1,4
215	13	25,2	1,377	0,15395	10,5247	20	16,1	3,6
225	17	15,2	0,830	0,28269	19,3077	37	35,4	1,6
235	18	5,2	0,284	0,38361	26,2005	55	61,6	-6,6
245	31	4,8	0,262	0,38568	26,3419	86	87,9	-1,9
255	22	14,8	0,808	0,28737	19,627	108	107,5	0,5
265	12	24,8	1,355	0,15822	10,806	120	118,3	1,7
275	5	34,8	1,901	0,06562	4,4818	125	122,8	2,2

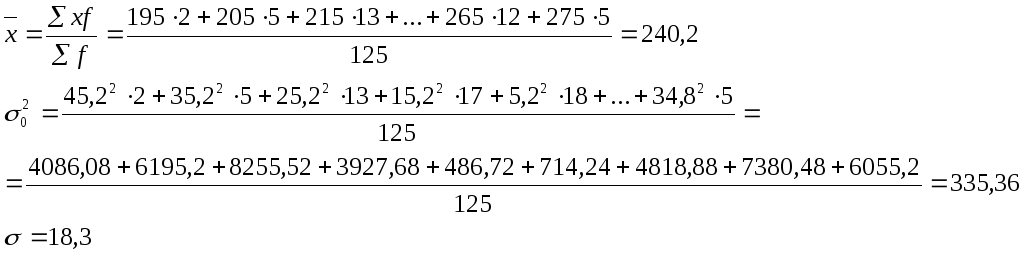
; постоянное число 68,30

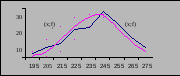
Рис. 6. Кривые фактического и нормального распределения

Критерии согласия.

Математическая статистика дает несколько показателей, по которым можно судить, на сколько фактическое распределение согласуется с нормальным. Эти показатели называются критериисогласия.

Критерий согласия Колмагорова (критерий ) определяется путем деленияmaxразности коммулятивных частот на корень квадратный из числа наблюдений:

, где d– максимальное отклонение фактической частоты от фактической частоты;

n– число наблюдений.

По приведенному примеру критерий =

По специальной таблице вероятности для критерия согласия определяют, что значение=0,59 соответствует вероятности 0,88. Это значит, что с вероятностью 0,88 можно судить об отклонении фактических частот от теоретических, которые являются случайными.