
Лекции по теоретической механике1 / Лекция №9
.docУравнения Лагранжа второго рода
Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения механической системы, составленные в обобщённых координатах:
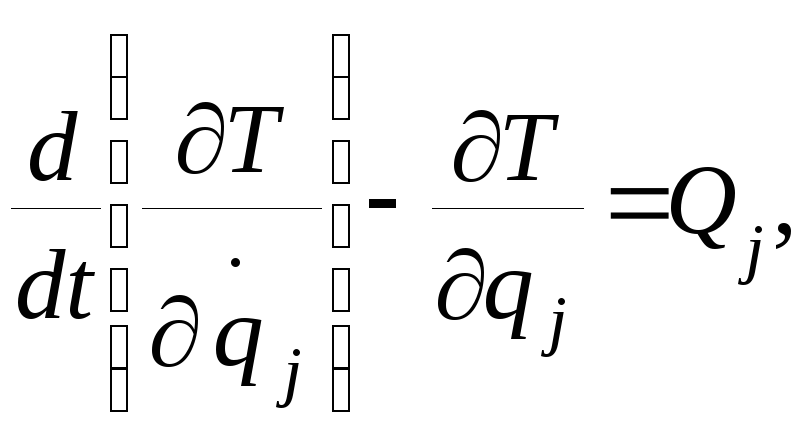
где j
– количество уравнений (j
= 1, 2, …, n),
n
– число степеней свободы механической
системы, T
– кинетическая энергия системы, qj
– обобщённая координата,
![]() – обобщённая скорость, Qj
– обобщённая сила. Если qj
= x
(м), то
– обобщённая скорость, Qj
– обобщённая сила. Если qj
= x
(м), то
![]() (м/с);
если qj
= φ
(рад), то
(м/с);
если qj
= φ
(рад), то
![]() (рад/с).
(рад/с).
Вычисление обобщённых сил
Если система имеет n степеней свободы, то у неё n обобщённых координат, независимых друг от друга (q1, q2, …, qn) и n возможных перемещений (δq1, δq2, …, δqn). Сумма элементарных работ, приложенных к системе сил, на возможные перемещения системы равна
![]() .
.
Обобщёнными силами называются коэффициенты, стоящие перед соответственными возможными перемещениями. Так как обобщённые координаты не зависят друг от друга, то для определения обобщённой силы системе необходимо сообщить возможные перемещения, соответствующие координатам, а все остальные возможные перемещения принять за нуль, то есть для определения Q1 необходимо, чтобы δq1 ≠ 0, δq2 = 0, δq3 = 0, …, δqn = 0, тогда
![]()
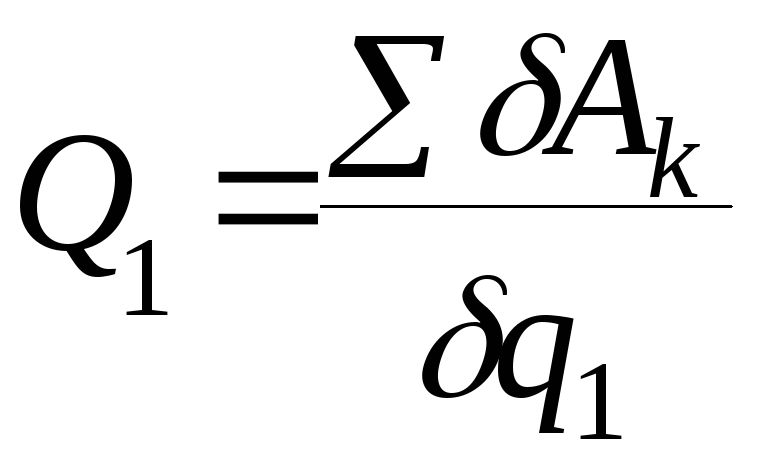 .
.
Размерность обобщённых сил зависит от размерности обобщённых координат: если qj = x (м), то Qj – сила (Н); если qj = φ (рад), то Qj – момент (Н∙м).
Пример 1.
Составить
дифференциальное уравнение груза,
перемещаемого вверх по гладкой наклонной
плоскости под действием силы
![]() .
.
Д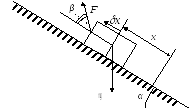 ано:
m,
α,
β.
ано:
m,
α,
β.
Решение:
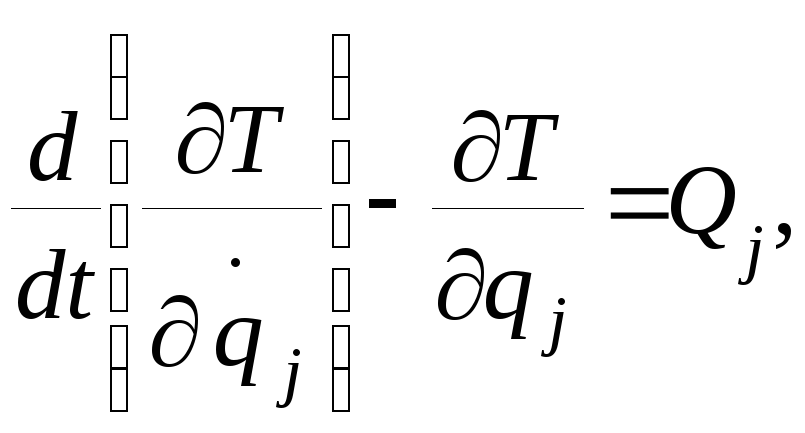
 n
= j
= 1, q
= x,
n
= j
= 1, q
= x,
![]()

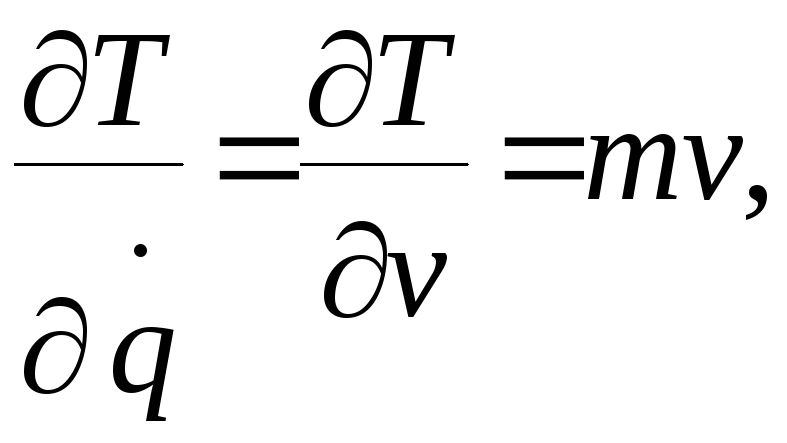
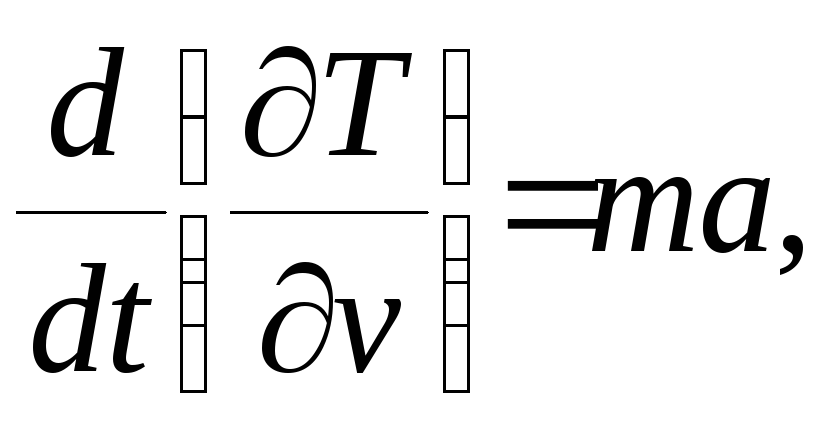
определим обобщённую силу Q; для этого составим сумму элементарных работ приложенных сил на возможное перемещение груза:
![]()
![]()
подставляем в уравнение Лагранжа:
![]()
дифференциальное уравнение движения груза имеет вид:
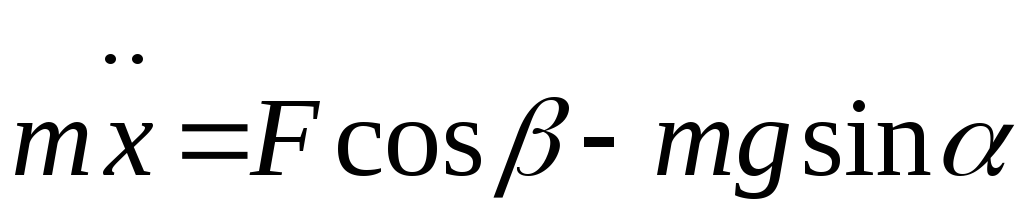 .
.
План решения задач с помощью уравнений Лагранжа второго рода.
-
Определить число степеней свободы механической системы и выбрать удобные обобщённые координаты.
-
Вычислить кинетическую энергию системы в её абсолютном движении и выразить её через обобщённые координаты qj ,
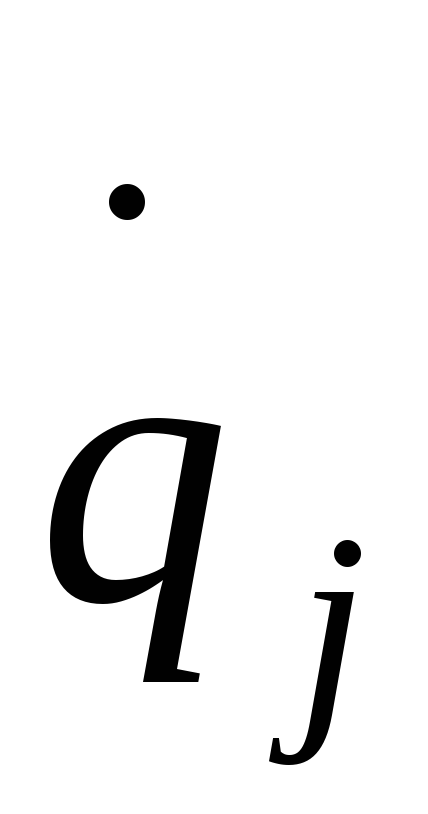 .
. -
Вычислить все производные в левой части уравнений.
-
Определить обобщённые силы Qj, соответствующие выбранным координатам.
-
Подставить всё в уравнения Лагранжа.
Пример 2.
С оставить
дифференциальное уравнение движения
механической системы и определить закон
движения этой системы при заданных
массах тел: m1,
m2,
m3.
Считать, что каток катится без скольжения
и пренебречь трением качения.
оставить
дифференциальное уравнение движения
механической системы и определить закон
движения этой системы при заданных
массах тел: m1,
m2,
m3.
Считать, что каток катится без скольжения
и пренебречь трением качения.
Решение:
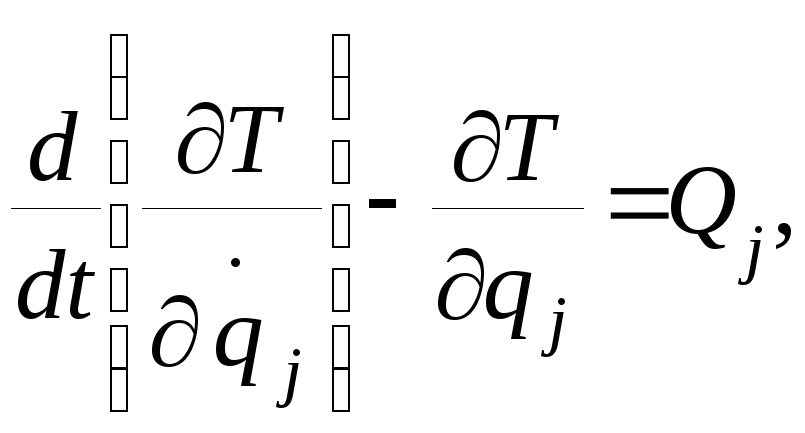
n
= j
= 1, q
= x,
![]() v1
= vc,
v1
= vc,
T = T1 + T2 + T3,
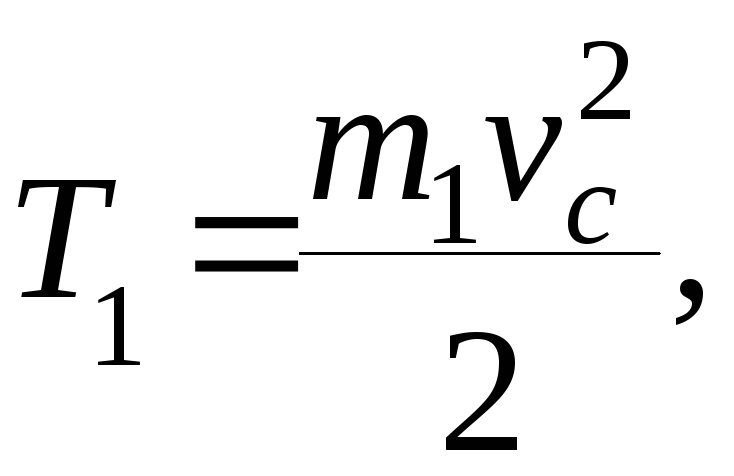
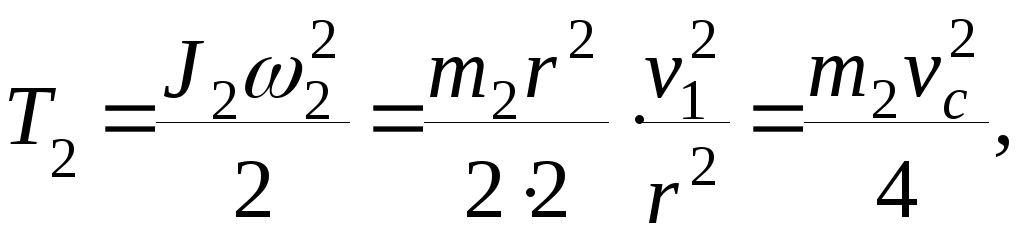
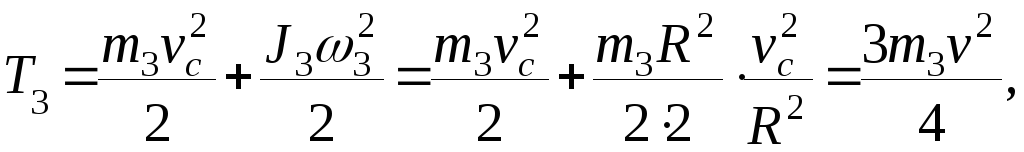
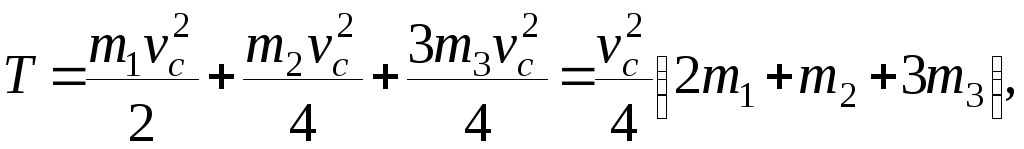
находим производные:
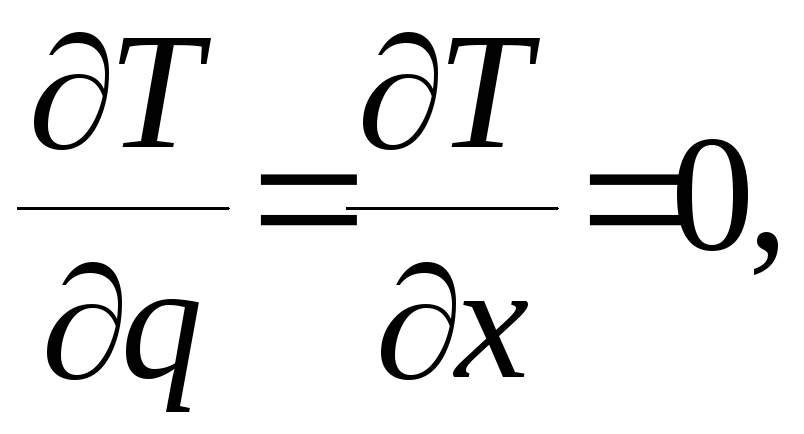
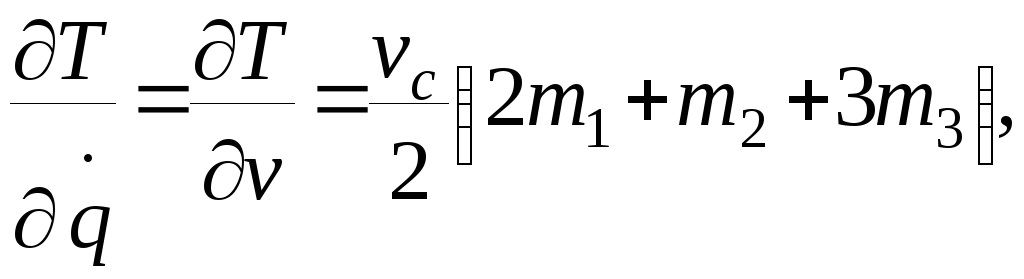
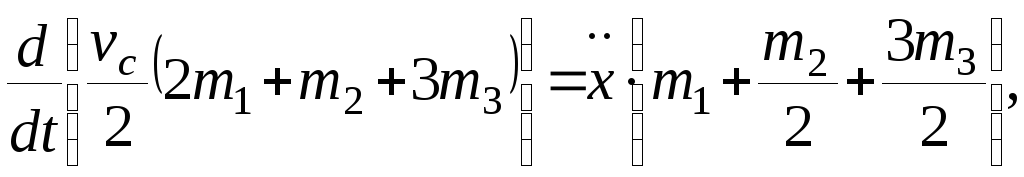
определим обобщённую силу Q, составляя сумму элементарных работ всех сил на возможные перемещения системы:
![]() δy
= δx,
δy
= δx,
![]() Q
= m1g,
Q
= m1g,
подставляем в уравнение Лагранжа:
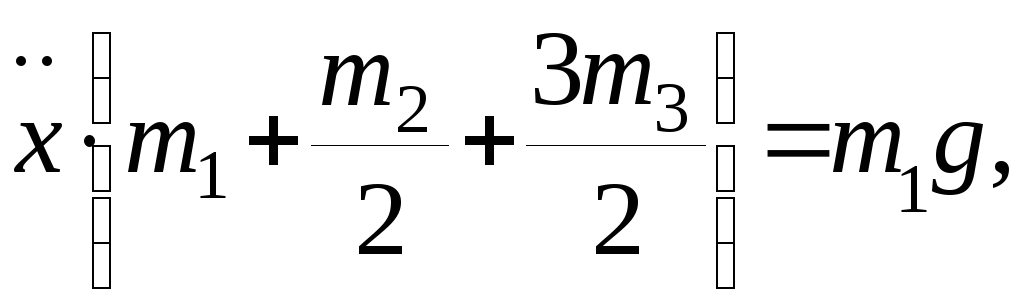
получали дифференциальное уравнение движения механической системы; для определения закона движения данной системы полученное выражение необходимо дважды проинтегрировать.
Пример 3.
Определить ускорение груза 1, применяя общие уравнения динамики.
Дано: m1, m2, m3.
Решение:
общее уравнение динамики:
![]()
зададим системе возможные перемещения:
![]()
![]()
![]()
![]()
![]()
найдём уравнения связи между всеми возможными перемещениями и другие связи между всеми ускорениями; связи между ними точно такие же, как и между соответствующими скоростями:
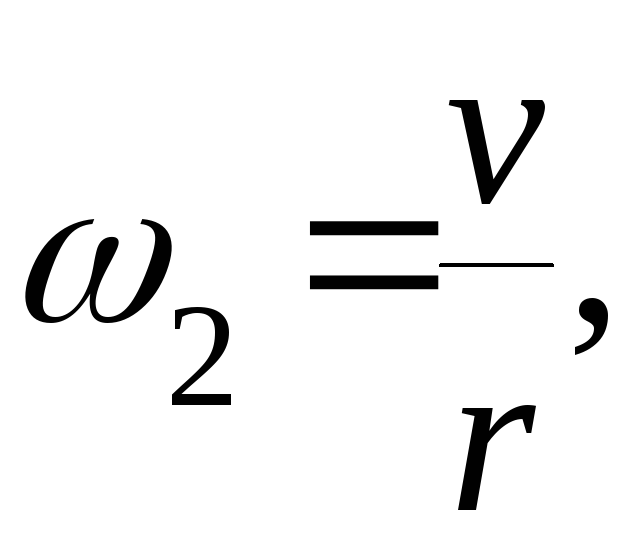

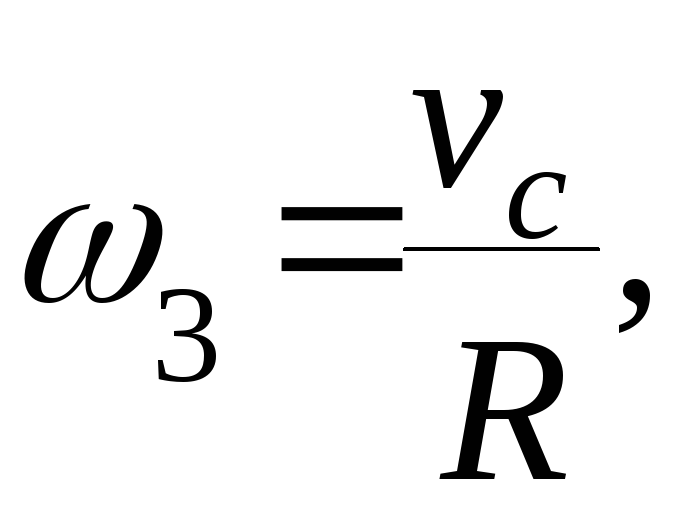 vc
= v,
vc
= v,

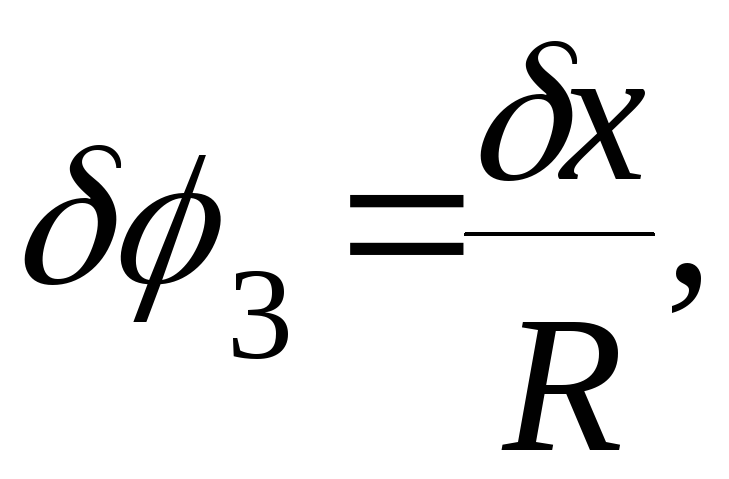 δx
= δy,
δx
= δy,
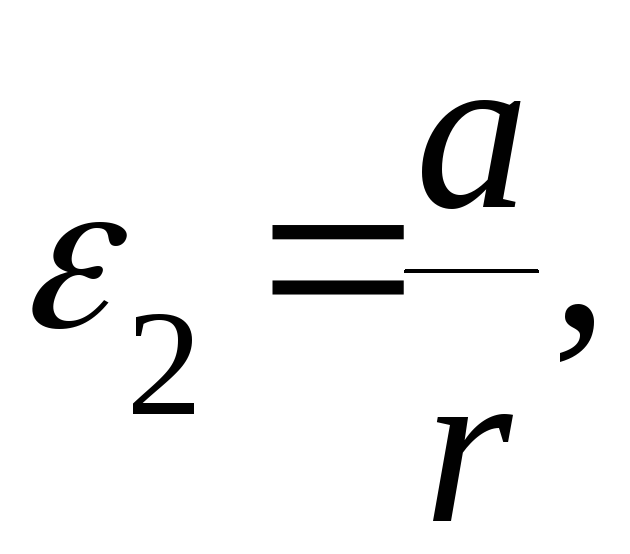
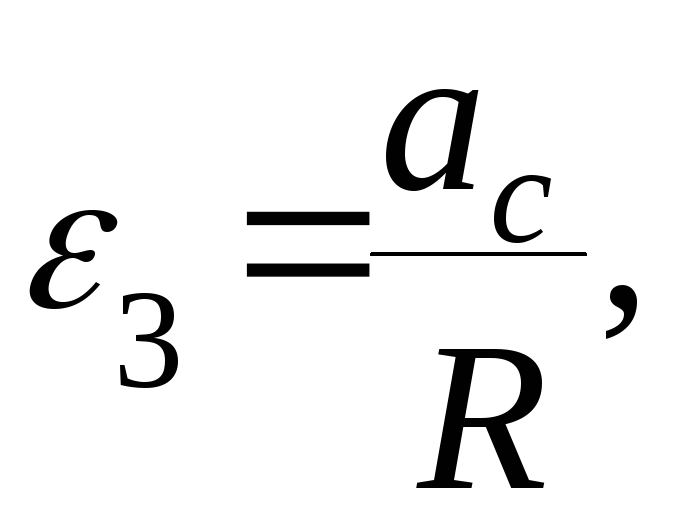 ac
= a,
ac
= a,
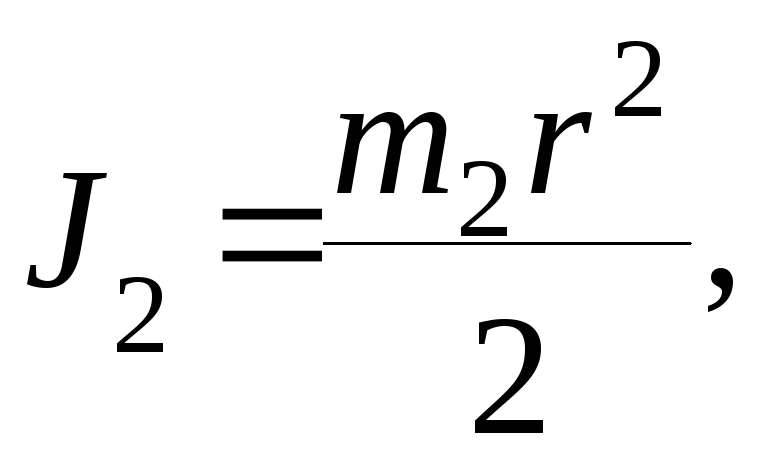

 δy
≠ 0,
δy
≠ 0,
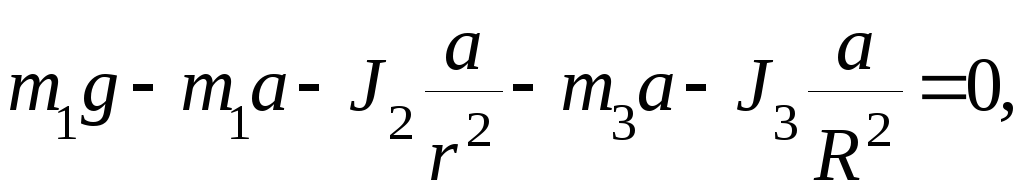

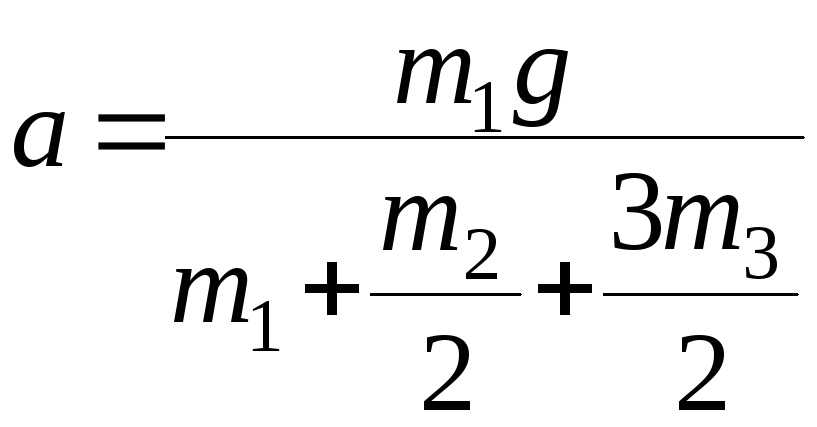 .
.
