
- •Часть 4
- •1.Функции нескольких переменных
- •1.1. Понятие функции двух переменных. Область определения
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные и частные дифференциалы первого порядка
- •1.4. Полное приращение функции и полный дифференциал
- •1.5. Применение полного дифференциала в приближенных вычислениях первого порядка
- •1.6. Частные производные сложной функции. Полная производная
- •1.7. Дифференциал сложной функции. Инвариантность формы первого дифференциала
- •1.8. Производная по направлению. Градиент
- •1.9. Частные производные и дифференциалы высших порядков
- •1.10. Дифференцирование функций, заданных неявно
- •1.11. Экстремум функции нескольких переменных. Необходимое условие
- •1.12. Достаточный признак экстремума
- •1.13. Наибольшее и наименьшее значение функции в замкнутой области
- •Вопросы для самопроверки
- •2. Двойной интеграл
- •2.1. Основные понятия и определения
- •2.2. Основные свойства двойного интеграла
- •2.3. Вычисление двойного интеграла в декартовых координатах
- •2.4. Вычисление двойного интеграла в полярных координатах
- •2.5. Вычисление объемов тел с помощью двойного интеграла
- •2.6. Вычисление площадей плоских фигур
- •2.7. Вычисление площадей поверхностей
- •2.8. Моменты инерции плоской фигуры
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3. Тройной интеграл
- •3.1 Задача, приводящая к понятию тройного интеграла
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •3.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.4. Вычисление объема тела с помощью тройного интеграла
- •3.5. Приложение тройного интеграла для вычисления массы тела
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •4.1. Основные понятия
- •4.2. Вычисление криволинейного интеграла II рода
- •4.3. Формула Грина
- •4.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5. Поверхностный интеграл II рода
- •5.1. Основные понятия
- •5.2. Вычисление поверхностного интеграла II рода
- •5.3. Формула Остроградского-Гаусса
- •5.4. Формула Стокса
- •5.5. Векторная запись формулы Стокса. Ротор вектора
- •5.6. Потенциальные векторные поля. Нахождение потенциала
- •5.7. Оператор Гамильтона. Векторные операции второго порядка
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Начала математического анализа
- •Часть 4
- •Подписано к изданию 02.05.06.
- •394026 Воронеж, Московский просп., 14
3.2. Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к вычислению трехкратного интеграла, т.е. последовательному вычислению трех определенных интегралов.
Пусть
областью интегрирования V
является тело, ограниченное снизу
поверхностью
![]() ,
сверху - поверхностью
,
сверху - поверхностью
![]() ,
причем (z1(x;
y)
≤ z2(x;
y)).
Область
является
проекцией тела на плоскость Оху
(рис.
15)
,
причем (z1(x;
y)
≤ z2(x;
y)).
Область
является
проекцией тела на плоскость Оху
(рис.
15)
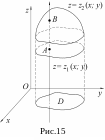
Область V называется правильной в направлении оси Oz, если любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х,у,z) имеет место формула
 .
.
Данная формула сводит вычисление тройного интеграла к вычислению двойного интеграла от однократного интеграла. Вычисление начинается с внутреннего интеграла по переменной z при постоянных х и у. Нижним пределом внутреннего интеграла является аппликата точки А точки входа прямой, параллельной оси Oz в область V, т. е. . Верхней границей является аппликата точки В - точки выхода прямой из области V, т.е. . Если граница области D (рис. 16) определена неравенствами
![]()
где
![]() и
и
![]() - непрерывные
на отрезке [а,b]
функции,
- непрерывные
на отрезке [а,b]
функции,
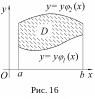
то, получаем формулу
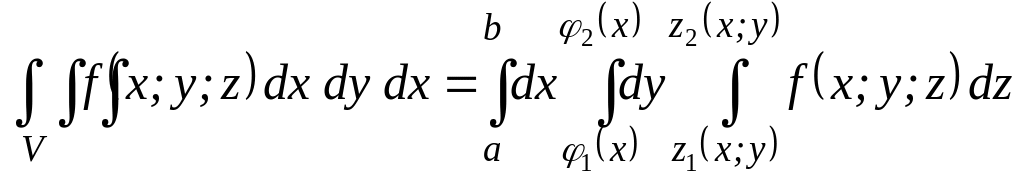 .
.
Стоит отметить, что порядок интегрирования в трехкратном интеграле может быть изменен, если область определяется как правильная относительно оси .
Пример
24.
Вычислить
![]() где
ограничена плоскостями
где
ограничена плоскостями
![]()
![]()
![]()
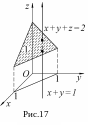
![]() (рис. 17).
(рис. 17).
Решение: Область является правильной в направлении оси Oz, а ее проекция на плоскость Оху является правильной в направлении оси Оу. По формуле перехода к трехкратному интегралу имеем:
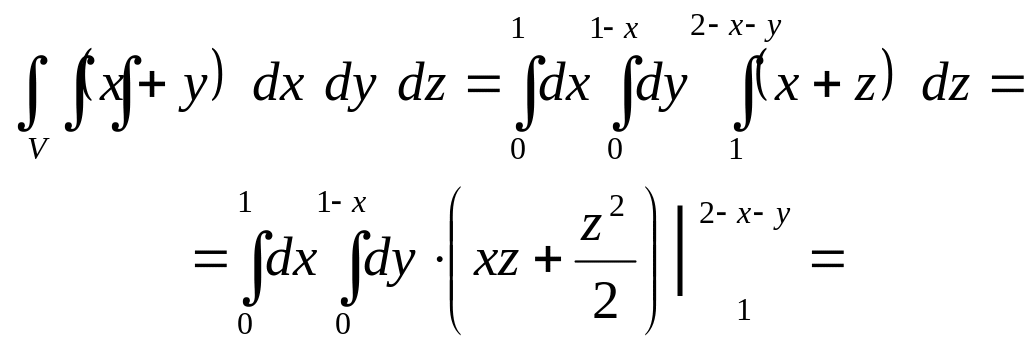
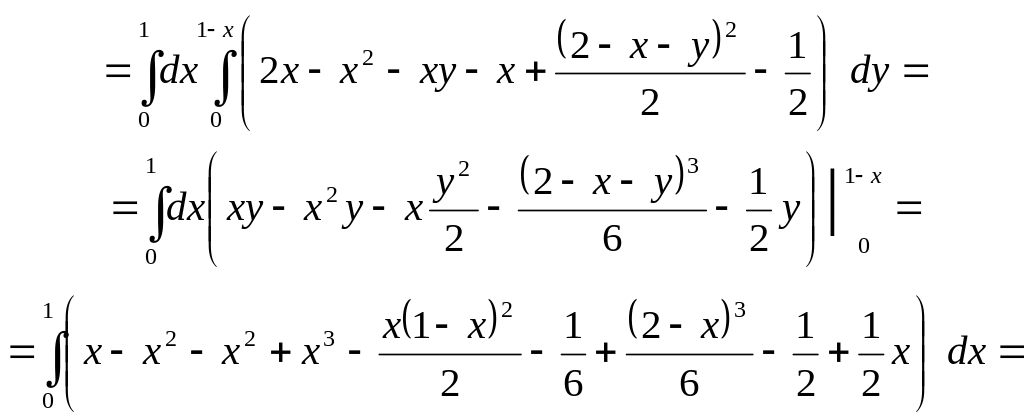
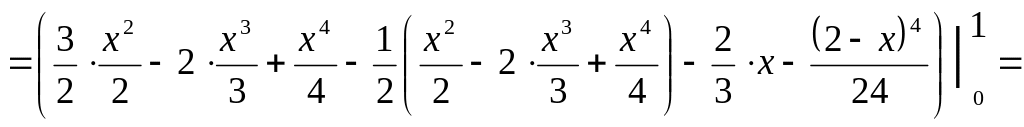
![]()
3.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
Замена переменных в тройном интеграле производится с помощью якобиана преобразования
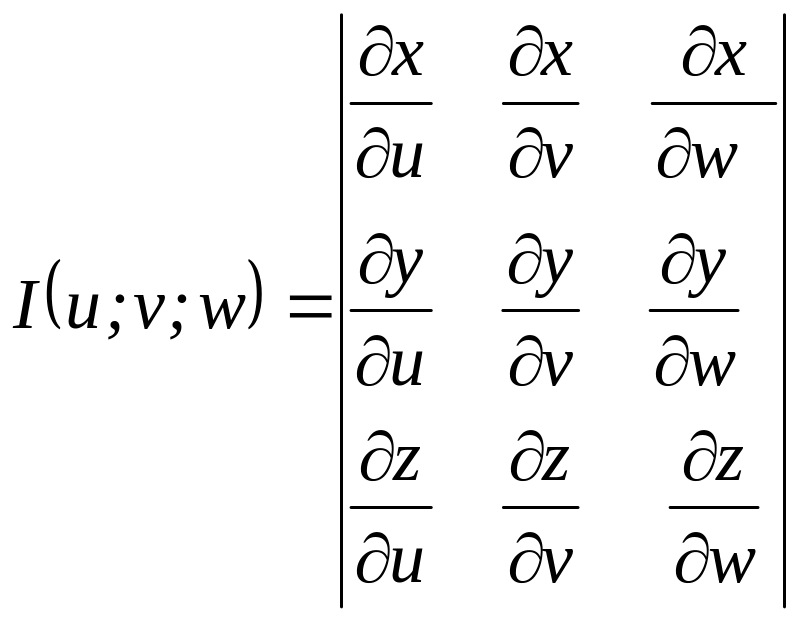 .
.
Пусть совершена подстановка x =φ(u;v;w), y=ψ(u;v;w), z=χ(u;v;w).
Если
эти функции имеют в некоторой области
V*
пространства Ouvw
непрерывные частные производные и
отличный от нуля определитель
![]() ,
то справедлива формула замены переменных
в тройном интеграле
,
то справедлива формула замены переменных
в тройном интеграле
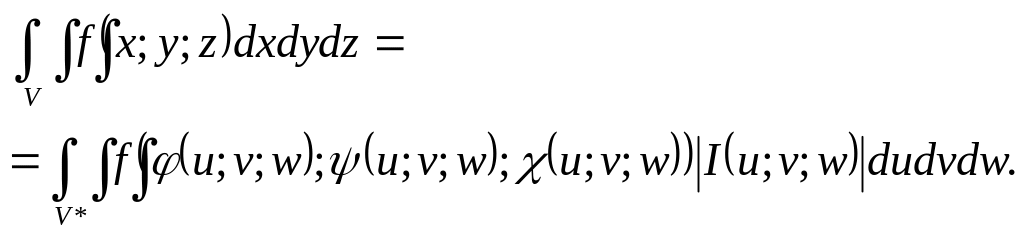
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты (рис. 18).
Положение точки М(х,у,z) в цилиндрических координатах определяется заданием трех чисел r, φ, z, где r –полярный радиус, т.е. длина радиуса-вектора проекции точки М на

плоскость
Оху
![]() ,
φ
–
полярный угол, образованный этим радиусом
- вектором с осью Ox
,
φ
–
полярный угол, образованный этим радиусом
- вектором с осью Ox
![]() ,
z
- аппликата точки М
,
z
- аппликата точки М
![]() .
.
Цилиндрические
координаты точки связаны с ее декартовыми
координатами следующими соотношениям0:
![]()
![]()
![]()
Якобиан преобразования равен
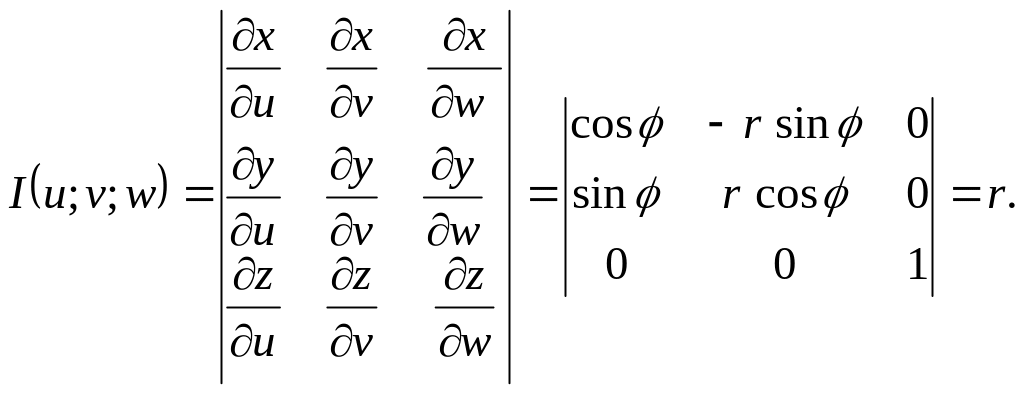
Формула замены переменных принимает вид
![]()
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования описывается в цилиндрических координатах более простым образом, а подынтегральная функция упрощается.
 Пример
25.
Вычислить
Пример
25.
Вычислить
![]() ,
где V
- область, ограниченная верхней частью
конуса
,
где V
- область, ограниченная верхней частью
конуса
![]() и
плоскостью
и
плоскостью
![]() .
.
Решение:
На рис. 19 изображена область
.
Уравнение конуса принимает вид
![]() ,
т. е.
,
т. е.
![]() .
Уравнение границы области D
х2
+ у2
= 1 запишется так: r
=
1. Используем равенство
.
Уравнение границы области D
х2
+ у2
= 1 запишется так: r
=
1. Используем равенство
![]() .
.
Прямая, параллельная оси Oz, входит в область D при z = r и выходит из нее при z = 1.
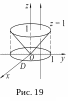
Согласно формуле перехода к трехкратному интегралу получаем:
![]()

Пример
26. Вычислить тройной интеграл
![]() где область
где область
![]() ,
ограничена поверхностями:
,
ограничена поверхностями:![]()
![]()
![]() .
.
Решение:
Запишем уравнение параболоида
![]() в цилиндрических координатах, используя
уравнения связи
в цилиндрических координатах, используя
уравнения связи
![]() ,
,
![]() :
:
![]() или
или
![]() .
.
Область
описывается неравенствами
![]() ,
,
![]() ,
,
![]() .
.

Сферическими
координатами точки
M(x,y,z)
пространства
Oxyz
называется
тройка чисел ρ,
φ,
θ,
где
ρ
-
длина
радиуса - вектора точки М
![]() ,
φ
-
угол,
образованный проекцией радиуса
- вектора
,
φ
-
угол,
образованный проекцией радиуса
- вектора
![]() на
плоскость Оху
и
осью Ох
,
θ
- угол отклонения радиуса-вектора
от оси Oz
на
плоскость Оху
и
осью Ох
,
θ
- угол отклонения радиуса-вектора
от оси Oz
![]() (рис.
20).
(рис.
20).
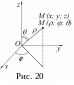
Сферические
координаты ρ,
φ,
θ
связаны с декартовыми x,
y,
z
соотношениями:
![]()
![]()
![]()
Якобиан преобразования при переходе к сферическим координатам равен
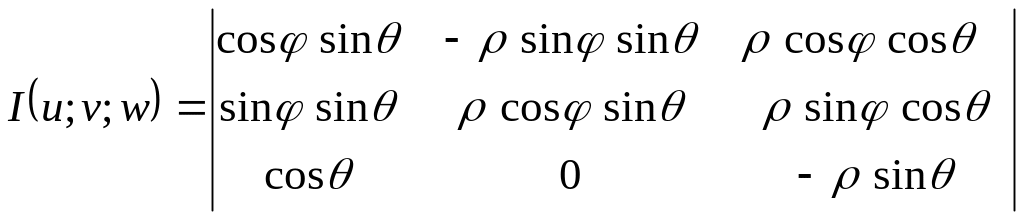 =
=
=![]() +
+
+![]() =
=
=![]() +
+
+![]() =
=
=![]()
Тройной интеграл в сферических координатах имеет вид
![]()
![]()
Пример 27. Вычислить тройной интеграл
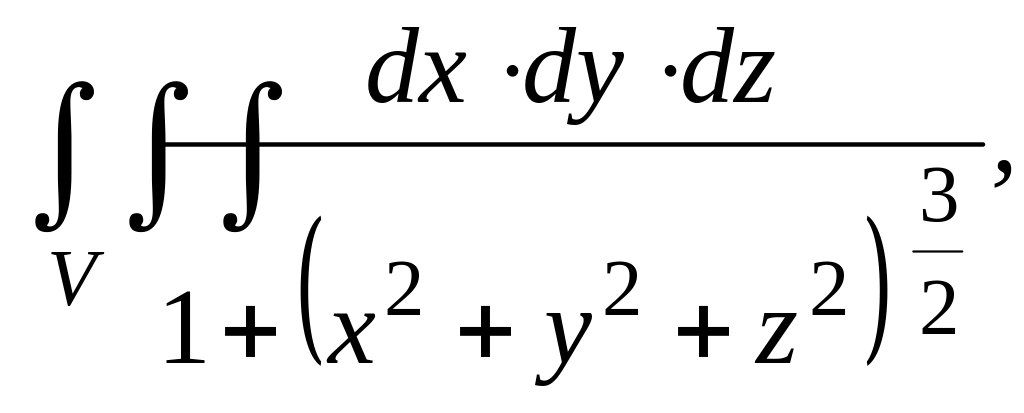
где V – шар x2 + y2 + z2 ≤ 1.
Решение: Используя якобиан преобразования, имеем
![]()
Граница
области V
- сфера и ее уравнение в сферических
координатах имеет вид ρ
= 1. Подынтегральная функция после замены
переменных примет вид
![]()
![]() Согласно
формуле тройного интеграла в сферических
координатах имеем
Согласно
формуле тройного интеграла в сферических
координатах имеем
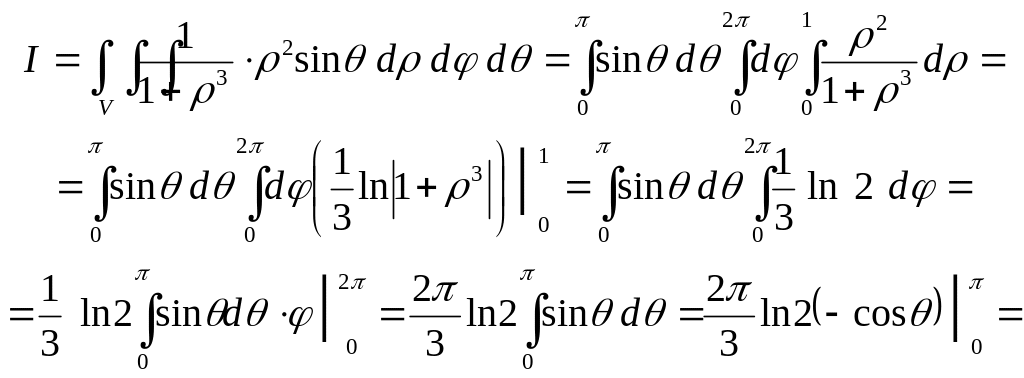
![]()
