Идеальными связями механической системы называют такие связи, при которых сумма элементарных работ сил реакций связей на любом возможном перемещении системы равна нулю.

8.3. Принцип возможных перемещений

Принцип возможных перемещений определяет условия равновесия точки или материальной системы, находящейся под действием заданной системы активных сил и при заданных связях. Для равновесия материальной системы (в некоторой инерциальной системе отсчета), находящейся под действием активных сил и подчиненной идеальным, голономным, неосвобождающим, стационарным связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на любом возможном перемещении системы из предполагаемого положения равновесия, т.е.

∑Fkδrk=0, (k=1,…,N).

9. ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ, ТЕОРИИ УДАРА

9.1. Устойчивость положения равновесия

Механическая система может совершать малые колебания только вблизи устойчивого положения равновесия. В положении равновесия обобщенные координаты системы принимают равными нулю, т.е. отсчитывают их от положения равновесия. Движение механической системы в общем случае считают колебательным тогда, когда все обобщенные координаты или часть из них изменяются не монотонно, а имеют колебательный характер, т.е. принимают нулевые значения по крайней мере несколько раз.

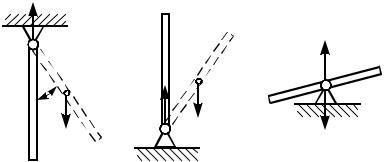
Рассмотрим стержень с горизонтальной осью вращения

(рис. 9.1).

48

R0	б)		в)
а)				_
0
				R0
C	C
	R0	_		0
ϕ
_	0	P		_
				P
P	ϕ=180ο
ϕ=0

Рис. 9.1

Положения равновесия стержня имеет место при ϕ=0° и ϕ=180°. В положении равновесия силы, приложенные к стержню, составляют уравновешенную систему сил. Для установления устойчивости положения равновесия стержня следует дать стержню достаточно малое начальное отклонение от положения равновесия. В отклоненном положении силы, действующие на стержень, уже не являются уравновешенными.

Если существует такое достаточно малое отклонение стержня от положения равновесия, при котором силы стремятся вернуть стержень в положение равновесия, то такое положение равновесия считается устойчивым (рис. 9.1, а).

В случае, когда силы еще дальше удаляют стержень от положения равновесия, положение является неустойчивым

(рис. 9.1, б).

Безразличным (рис. 9.1, в) называется такое положение равновесия, когда стержень, получив малое начальное отклонение от положения равновесия, остается в равновесии в новом отклоненном положении.

Рассмотренные положения равновесия стержня характерны не только для любого твердого тела, но и для любой механической системы.

При устойчивом положении равновесия система, выведенная из положения равновесия достаточно малыми возму-

49

щениями в виде начальных отклонений и скоростей, которые сообщаются всем точкам системы или их части, совершает колебания около положения равновесия или приближается к нему без колебаний. При неустойчивом положении равновесия случайные возмущения приводят к тому, что система при дальнейшем движении все дальше и дальше удаляется от положения равновесия [26].

Условимся обобщенные координаты q1, q2, … , qn принимать равными нулю в положении равновесия, т.е. отсчитывать их от положения равновесия системы. В общем случае из на-

чальных значений обобщенных координат q10 , q20 , , qn0 и начальных обобщенных скоростей q10 , q20 , , qn0 состоит началь-

ное возмущение системы.

Если для всякого как угодно малого положительного числа ε можно выбрать два других малых положительных числа η1, η2 таких, что при начальных возмущениях, удовлетворяют

условиям qi0 <η1 , qi0 <η2 , в дальнейшем движении механиче-

ской системы выполняются условия qi(t) <ε для каждой обобщенной координаты, то равновесие системы называется устойчивым.

В положении равновесия механической системы каждая обобщенная сила Qi равна нулю [26]. Для случая потенциального силового поля обобщенные силы выражаются через потенциальную энергию по формулам

Qi=–∂ П/∂ qi, i=1, 2, …, n.

Следовательно, в положении любого равновесия

∂ П/∂ qi=0, и поэтому потенциальная энергия при этом достигает своего экстремального значения [26].

9.2. Колебания системы с одной степенью свободы

Механическая система с одной степенью свободы в случае голономных, идеальных, неосвобождающих связей имеет

50

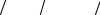
одну обобщенную координату q, и ее движение описывается уравнением Лагранжа:

d dt(∂T ∂q)− ∂T ∂q = Q .	(9.1)

Обобщенная сила Q состоит из трех частей:

Q=QП+QФ+QВ. (9.2)

Обобщенная сила потенциальных сил выражается через

потенциальную энергию по формуле QП=–∂П/∂q.

QФ – обобщенная сила от действия сил сопротивления. Часть обобщенной силы QВ получается от так называе-

мых возмущающих сил, зависящих прежде всего от времени. Рассмотрим малые колебания системы с одной степенью

свободы под действием одних потенциальных сил [26]. Считаем, что сил сопротивления и возмущающих сил нет. Такие колебания называются собственными, или свободными. В да н- ном случае малых колебаний системы получим линейное дифференциальное уравнение для обобщенной координаты q, в.

Выражение для кинетической энергии можно представить в

виде

T = 1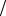2aq2 ,

где a – называется коэффициентом инерции. Потенциальная энергия определяется в соответствии с выражением П(q)=1/2cq2, где c – коэффициент жесткости. Составляющие уравнения Лагранжа для этого случая имеют вид:

∂T∂q = 0, ∂T∂q = aq, ddt (∂T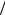∂q)= aq, ∂П∂q = cq .

Уравнение Лагранжа после подставки этих значений производных позволяет получить дифференциальное уравнение малых собственных колебаний системы с одной степенью свободы:

aq + cq =0 .	(9.3)

51

После деления обеих частей уравнения (9.3) наa и обозначения c/a=k2 получим дифференциальное уравнение собственных колебаний системы с одной степенью свободы в форме

q + k	2	q = 0 .	(9.4)

Постоянная величина k называется круговой, или циклической, частотой колебаний. Для прямолинейных колебаний материальной точки (рис. 9.2), на которую действует сила Fx=– c0x, имеем x + k2 x = 0 , где k2=c0 /m.

0

F M

x

x

Рис. 9.2

Решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами (9.4) будем

искать в виде q=eλt. После подстановки этого выражения в

(9.4) получаем характеристическое уравнение λ2+k2=0. Последнее квадратное уравнение имеет два чисто мни-

мых корня λ1,2=±ki. Решение уравнения (9.4) можно представить в виде

q=C1cos(kt)+C2sin(kt). (9.5)

Производная от этого выражения позволяет определить обобщенную скорость

	q = −C1k sin(kt)+ C2k cos(kt).		(9.6)
Из начальных условий определяются произвольные по-
стоянные C1	и C2: t = 0, q = q0 , q = q0 , где q0 и		q0 – начальные

значения обобщенной координаты и обобщенной скорости. Используя выражения для q и q при t=0, получаем

C1 = q0 ,C2 = q0 k . Подставляя их значения в (9.5), имеем:

q = q cos(kt)+	q0	sin(kt).	(9.7)
0	k

52