Т.к. S = 4000

см2, g =100

см

,

ρд = 0,8

г

,

ρв =1

г

,

H =50

см, имеем

сек

2

см3

см3

4000

1000

0,64

2500

г см2

кг м2

A =

=3,20

=3,20

Дж.

2

2

2

1

сек

сек

2.1.9.2. Вычисление пути по известной скорости

При изучении производной рассматривалась задача о мгновенной скорости. Если тело движется прямолинейно и его перемещение S является

функцией	времени, т.е. S = S(t), то производная	S (t)	задает в каждый
	мгновенную скорость V (t):	′
момент t			(2.33)
	V (t)= S (t).
	′

Пусть известна функция V (t) непрерывная на [t1 ,t2 ]. Нам нужно найти путь, пройденный телом за время от момента t = t1 до момента t = t2 . Очевидно, искомый путь S = S(t2 )− S(t1 ). Учитывая (2.33), делаем вывод, что функция

S(t) - это первообразная функции V (t), и так как V (t)				непрерывна на [t1 ,t2 ],
то по формуле (2.12) Ньютона-Лейбница t∫2 V (t)dt = S(t2 )− S(t1 ), т. е.
t1
S = t∫2 V (t)dt .							(2.34)
t1	равна V = (3t2			− 2t) м/с. Найти путь
Задача. Скорость точки в момент t
S , который преодолела точка, двигаясь прямолинейно, за время, равное 4 с,
прошедшее от начала движения.
Воспользуемся формулой (2.34), где V = 3t2 − 2t , t					= 0, t	2	= 4 :
				1
S = ∫4 (3t2 − 2t)dt = (t3 − t2 )			4 = 64 −16 = 48 (м).
0			0

2.2.Несобственные интегралы

Впервом разделе главы 2 рассматривались определенные интегралы. В определении этого понятия фигурировал предел последовательности интегральных сумм, который не обязательно существует. Отмечалось, что непрерывные на отрезке [а;b] функции интегрируемы на этом отрезке.

Оказывается есть и другие классы интегрируемых функций. Например, если функция y = f (x) имеет внутри [а;b] разрыв первого рода (с конечным

скачком в точке разрыва), а в остальных точках [а;b] непрерывна, то ∫b f (x)dx

a

тоже существует. При этом для его вычисления можно использовать формулу Ньютона-Лейбница (не на всем отрезке, а на его частях). Продемонстрируем вышесказанное на примере. Рассмотрим функцию

74

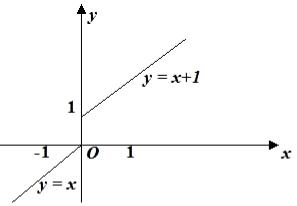
( ) х при х 0, y = f x = x +1 при х 0..

Очевидно, функция f (x) непрерывна при x (− ∞,0) и при x (0,∞), а

		в точке x0	= 0	имеет	разрыв	первого
		рода, рис. 2.30.
		Вычислим	∫1 f (x)dx .		По свойству 7
			−1
		определенных		интегралов		можно
						записать
		∫1 f (x)dx = ∫0 f (x)dx + ∫1 f (x)dx = ∫0 хdx +
		−1	−1		0	−1
	Рис. 2.30	1
		∫(x +1)dx ,	(вместо		функции f (x)
		0

подставили выражения, которыми f (x) задается слева и справа от точки х0 = 0). В последнем выражении каждое слагаемое можно вычислить по формуле Ньютона-Лейбница, т.е.

1

f (x)dx =

x2

0

x2

1

1

1

∫

−1

+

+ x

0

= 0

−

+

+1

− 0

=1.

−1

2

2

2

2

на [а;b] есть

В некоторых случаях,

например, если у функции f (x)

точки разрыва второго рода, определенный интеграл может и не существовать. Используя понятие определенного интеграла, все же удается описать такие ситуации. Кроме того, распространяют «понятие определенного интеграла» на бесконечный промежуток интегрирования. В таких случаях полученные интегралы называют несобственными.

2.2.1. Несобственные интегралы I рода

Рассмотрим функцию y = f (x), непрерывную на полуоси [a,+∞). Для

любого b (b>a ) существует ∫b	f (x)dx , очевидно зависящий от	верхнего
a
предела b. Устремим b к ( + ∞).		f (x) на
Определение. Несобственным интегралом I рода от функции
полуоси [a,+∞), обозначаемым ∞∫ f (x)dx , называют blim→+∞ ∫b f (x)dx , т. е.
a	a
+∞∫ f (x)dx = blim→+∞ ∫b f (x)dx .		(2.35)
a	a

Если этот предел существует, то несобственный интеграл называют сходящимся (его значение равно полученному пределу). Если же предел бесконечен или не существует, то несобственный интеграл называют расходящимся.

75

Пример 2.22. Исследовать несобственный интеграл +∞∫																dx			.
													b		1		x
+∞ dx					b −	1			3		2						3
					∫x	3	dx			x	3								3
По определению ∫3				= blim→+∞											= blim→+∞
		x						= blim→+∞	2				1				2
1					1

			3
b	2	−		1				= +∞.
			2

Делаем вывод, что исследуемый интеграл расходится.

Несобственный интеграл (2.35) называют несобственным интегралом с

бесконечным верхним пределом.	f (x) непрерывна при −∞<		x ≤ b , то по
Аналогично, если функция
определению
∫b f (x)dx = alim→−∞ ∫b		f (x)dx .	(2.36)
−∞	a

Если этот предел существует и конечен, то несобственный интеграл с бесконечным нижним пределом, стоящий в левой части равенства (2.36), называется сходящимся и его значение определяется формулой (2.36). Если же этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

Пример 2.23. Исследовать несобственный интеграл −∫1 dx .

−∞ x2

−1 dx

−1

−2

x−1

−1

1

−1

По формуле (2.36) ∫

∫

x

dx

=

−

=

2

= alim→−∞

alim→−∞

−1

a

= alim→−∞

x

a

−∞ x

а

		1		=1 + 0 =1. Делаем вывод, что интеграл сходится и равен 1:
= lim 1 +		a
a→−∞

	−∫1 dx2 =1.
	−∞ x
Если	функция f (x) непрерывна	на всей числовой оси, то можно
рассмотреть	несобственный интеграл	∞∫ f (x)dx . Для его определения
		−∞

привлекают уже рассмотренные ранее несобственные интегралы (2.35) и (2.36). Выбирают произвольное число c R и полагают по определению

∞∫ f (x)dx = ∫c		f (x)dx + +∞∫ f (x)dx .	(2.37)
−∞	−∞	c
Если независимо от выбора c оба несобственных интеграла, стоящие в
правой части равенства (2.37), сходящиеся, то			∞∫ f (x)dx сходится и равен их
			−∞

сумме (по формуле (2.37)). Если же хотя бы один из несобственных

интегралов в правой части (2.37) расходится, то ∞∫ f (x)dx – расходящийся.

−∞

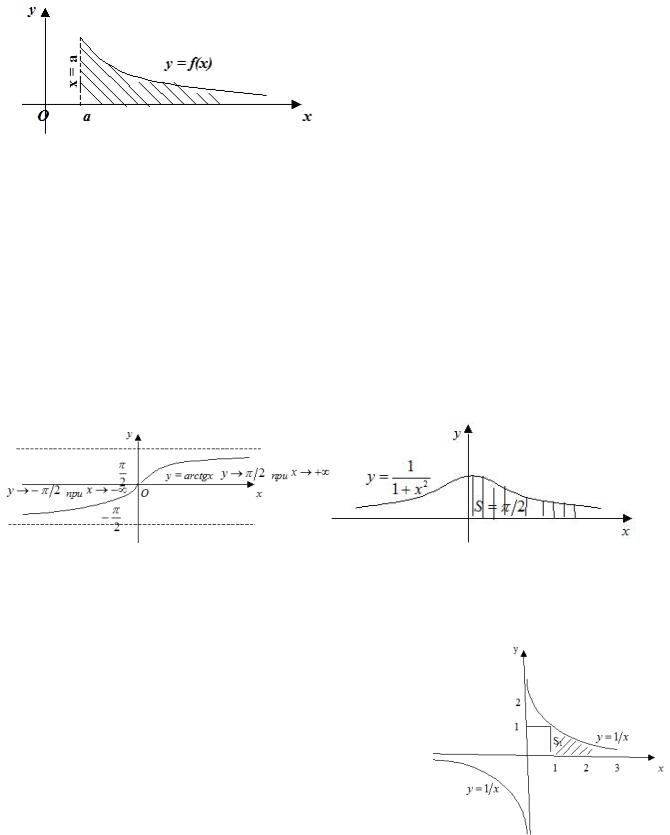
Геометрически для неотрицательной на [a;+∞) функции f (x)

76

несобственный интеграл	+∞∫ f (x)dx	представляет собой			площадь
	a
криволинейной фигуры, ограниченной графиком функции y = f (x), осью Ox
и прямой x = a (рис. 2.31).		Здесь фигура		не	ограничена
		справа	никакой	вертикальной
		прямой.
		Приведем несколько примеров
		вычисления		несобственных

интегралов и дадим геометрическую

Рис. 2.31

+∞ dx

интерпретацию некоторых из них.

Пример 2.24.

Найти

или сделать вывод о его расходимости

∫0 1+ x2

1

(здесь подынтегральная функция f (x)=

).

1+ x2

b

+∞ dx

b

dx

π

π

∫

2 = blim→+∞

∫

1+ x

2 = blim→+∞ arctgx

blim→+∞(arctgb − arctg0)=

2

− 0 =

2

0 1+ x

0

0

(рис.

2.32,

поясняет,

почему

lim arctgb = π ). Данный

несобственный

b→+∞

2

интеграл сходится, а площадь S (рис. 2.33) конечна ( S = π

кв. ед.).

2

Рис. 2.32

Рис. 2.33

Пример 2.25. Найти +∞∫dx или доказать его расходимость.

1 x

По определению

+∞1	b		dx			b		= blim→+∞(lnb − ln1)=
∫	dx = blim→+∞	∫
				= blim→+∞ ln x		1
1 x		1	x
			= lim ln b = +∞.
				b→+∞
	Таким образом, данный интеграл расходится,
а изображенная на рис.					2.34 площадь S1 –
бесконечна ( S1		= +∞).						Рис. 2.34

77

Пример 2.26 Найти

+∞dx

или доказать его расходимость.

∫1 x2

1

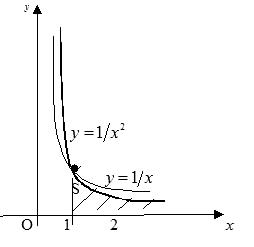
Сделаем рис. 2.35, на котором изобразим графики функций

y =

и

x2

y = 1 .

x

1

Мы видим, что функция

y =

x2

убывает быстрее,

чем

y =

1 . Из рис.

x

S ,

2.35 видно, что площадь

ограниченная

сверху

кривой

y =

1

,

x2

будет меньше, чем соответствующая

Рис. 2.35

площадь,

ограниченная кривой y =

1 .

1

x

Выясним, будет ли эта площадь конечной, то есть будет ли сходиться +∞∫

dx .

2

По формуле (2.35)

1

x

dx

b

+∞ 1

dx = lim

b

1

1

1

1

∫

∫

2

= lim

−

= lim

−

− −

= lim

−

+1

=1.

2

x

b→+∞

x

b→+∞

x

1

b→+∞

b

1

b→+∞

b

1

1

Таким образом,

+∞∫

1

dx - сходится, а площадь S - конечна ( S = 1 кв.ед.).

2

1

x

Пример

2.27.

Вычислить

несобственный

интеграл

+∞∫cos xdx

или

установить его расходимость.

0

b

+∞∫cos xdx = lim sin x

= lim(sin b −sin 0)= lim sin b.

0

b→+∞

0

b→+∞

b→+∞

Этот

предел

не

существует

(sin x

при

x → +∞ не

стремится

к

определенному значению, так как значенияsin x колеблются в промежутке от –1 до 1). Следовательно, несобственный интеграл расходится.

Иногда достаточно установить, сходится данный интеграл или расходится и оценить его значение. Для этого могут быть полезны следующие теоремы, которые мы приведем без доказательства, а применение проиллюстрируем примерами. Приводимые ниже теоремы называют

признаками сравнения.		x [a,+∞)
Теорема (Первый признак сравнения.) :	Если для всех
+∞	(x)dx сходится, то	+∞	f (x)dx
выполняются неравенства 0 ≤ f (x)≤ϕ(x) и ∫ϕ		∫
a		a

78

также сходится, и

+∞	+∞
∫	f (x)dx ≤ ∫ϕ(x)dx .

aa

Пример 2.28. Исследовать, сходится ли интеграл +∞∫e−x2 dx .

1

Заметим, что

∫e−x2 dx

относится к числу так называемых «неберущихся».

Воспользуемся

первым

b

признаком

сравнения.

Найдем

+∞

−x

dx = lim

b

−x

= lim(−e

−x

)

= lim(−e

−b

+e

−1

)=

1

. Так

как

при x ≥1

∫e

∫e

dx

1

e

1

b→+∞

1

b→+∞

b→+∞

выполняется неравенство e−x2

≤ e−x , то +∞∫e−x2 dx тоже сходится и его значение

1 .

1

меньше, чем

e

Теорема

(Второй

признак

сравнения).

Если

для

всех

x ( x ≥ a )

+∞

выполняется неравенство

0 ≤ϕ(x)≤ f (x), причем

∫ϕ(x)dx

- расходится, то

a

расходится и интеграл +∞∫ f (x)dx .

a

Пример 2.29. Исследовать интеграл +∞∫ x +1dx .

1 x3

Заметим,

что

x +1

>

x

=

1

>

0, при

x [1,+∞). Так

как

x3

x3

x

+∞ dx

b −

1

b

= blim→+∞ (2

b − 2)= +∞,

2

∫

x

т.е. расходится,

то из

x

= blim→+∞

∫x

dx

=

blim→+∞ 2

1

1

x

1

1

неравенства

+1

>

по

второму

признаку сравнения следует,

что

x3

x

исследуемый интеграл тоже расходится.

Замечание. Очевидно для несобственных интегралов ∫b f (x)dx тоже можно

−∞

сформулировать аналогичные теоремы сравнения.

у

				2.2.2. Несобственные интегралы II рода
				Пусть функция y = f (x)	непрерывна		в
				полузамкнутом интервале [a,b),	а	lim f (x)	не
						x→b−0
				x существует или равен бесконечности,		рис. 2.36.
		а	с b
			Рис. 2.36

79

Для любой точки с (a,b) существует ∫c	f (x)dx , зависящий от c . Устремим c
a

	c	(x)dx . Этот предел обозначают
к b слева и будем искать	сlim→b−0 ∫ f
	a
называют несобственным интегралом II рода, то есть
∫b f (x)dx = clim→b−0 ∫c f (x)dx .
a		a

∫b f (x)dx и

a

(2.38)

Если предел, стоящий в правой части равенства (2.38), существует, то несобственный интеграл II рода называют сходящимся. Если же этот предел равен бесконечности или не существует, то несобственный интеграл

расходится. Например, рассмотрим

∫0 dx

. Здесь f (x)=

1 , она непрерывна при

−2

x

x

x [− 2,0), а lim

1

= ∞. Значит,

∫0 dx

–

это несобственный интеграл II рода.

x→0

x

−2 x

0

dx

c

dx

c

По формуле (2.38) ∫

x

= limc→−0

∫

x

= limc→−0 ln

x

− 2

= limc→−0(ln

c

− ln 2)= −∞. Это

−2

−2

означает, что ∫0 dx расходится.

−2 x

По формуле, аналогичной (2.38), можно дать определение несобственного интеграла II рода на отрезке [a,b] от функции, непрерывной

на (a,b], у которой lim f (x) равен бесконечности или не существует:

x→a+0

b	b
∫ f (x)dx = clim→a+0	∫ f (x)dx .	(2.39)
a	c

При этом такой несобственный интеграл сходится, если предел в правой части существует и расходится в противном случае. Например,

рассмотрим ∫5

dx

.

Здесь

f (x)=

1

непрерывна

при x (1,5]

и

x −1

x −1

1

1

dx

lim

= +∞. Поэтому ∫5

– это несобственный интеграл II рода. По

x→1+0

x −1

1

x −1

формуле (2.39):

5

5

dx

5

−1

1

= lim

(x −1)

2 dx = lim

2(x −1)2

= lim(4 − 2

c −1)= 4 − 0 = 4

,

1

x −1

∫

c→1+0

∫

c

→1+0

c→1+0

т.е. несобственный интеграл сходится и равен 4.

Если функция y = f (x)

непрерывна во всех точках отрезка [a,b] кроме

точки

x0 (a,b),

являющейся точкой

разрыва II рода (хотя бы один из

односторонних

пределов

функции

f (x) в

этой точке бесконечен или

не

80

существует), то ∫b f (x)dx тоже является несобственным интегралом II рода и

a

по определению представляется в виде

b	x0	f (x)dx +	b
∫ f (x)dx = ∫			∫ f (x)dx .	(2.40)
a	a		x0

Такой интеграл является сходящимся, если сходятся оба интеграла в правой части формулы (2.40). В противном случае ∫b f (x)dx расходится. Аналогично,

	a
∫b	f (x)dx представляется в виде суммы нескольких несобственных
a

интегралов, если в (a,b) есть несколько точек разрыва II рода функции f (x). В виде суммы двух несобственных интегралов II рода записывается

∫b f (x)dx	и в случае, когда f (x) непрерывна в (a,b), а пределы			f (x) в обоих
a
концах	a	и b не являются конечными: ∫b	f (x)dx = ∫с f (x)dx + ∫b		f (x)dx , где
		a	a	с
точка с	-	произвольная точка интеграла (a,b).

Заметим, что обозначение несобственного интеграла II рода такое же, как и определенного. Чтобы отличить их друг от друга, нужно изучить подынтегральную функцию f (x) на отрезке интегрирования [a,b]. Если f (x)

непрерывна на [a,b] или имеет на [a,b] конечное число точек разрыва I рода,

то интеграл определенный. В противном случае – интеграл несобственный и его нужно вычислять, используя одну из формул, приведенных выше.

Если функция

Рис. 2.37

y = f (x) неотрицательна на [a,b], и ∫b f (x)dx является

a

несобственным, то он тоже может быть интерпретирован как площадь фигуры, имеющей незамкнутую границу. В последнем рассмотренном примере получилось, что

5		dx
∫1					= 4 .				Построив график функции
		x −1
f (x)=				1					(рис. 2.37), делаем вывод, что
						x −1
площадь S							заштрихованной фигуры конечна

и равна 4 кв. ед.

Замечание. Для несобственных интегралов II рода тоже существуют теоремы сравнения, аналогичные признакам сравнения для несобственных интегралов I рода.

81