Нахождение общего решения
Общее решение при вызове dsolve будет получаться, если в списке deqns отсутствуют начальные или граничные условия.
Пример.
Решить уравнение
(a – некоторый параметр)
> dsolve(diff(diff(y(x),x),x)=a*diff(y(x),x)+y(x),y(x));
Как и следовало ожидать, общее решение содержит две произвольные постоянные _C1 и _С2. Кроме того, оно включает параметр a.
Решим то же уравнение с определенным значением параметра, например, a=4:
> dsolve(diff(diff(y(x),x),x)=4*diff(y(x),x)+y(x),
y(x));
В
теории линейных дифференциальных
уравнений вводится понятие «фундаментальная
система решений», которая играет роль
базиса пространства решений однородного
уравнения. Если функцию dsolve
запустить с параметром output=basis,
будет выведена эта самая фундаментальная
система решений. Например, для уравнения
получим
> dsolve(x^2*diff(y(x),x$2)+3*x*diff(y(x),x)+4*y(x)=0,y(x),output=basis);
Для записи общего решения нужно сложить функции, входящие в фундаментальную систему, предварительно их умножив на произвольные постоянные (C1 и C2):
Если
уравнение неоднородное (к примеру,
),
то помимо фундаментальной
системы решений соответствующего
однородного уравнения получим еще и
частное решение данного уравнения:
> dsolve(x^2*diff(y(x),x$2)+3*x*diff(y(x),x)+
4*y(x)=x,y(x),output=basis);
здесь
есть частное решение. Как известно,
общее решение неоднородного линейного
уравнения строится как сумма общего
решения соответствующего однородного
уравнения и какого-либо частного решения
данного неоднородного уравнения. Поэтому
в последнем примере общее решение
запишется в виде
.
Предпочтение
явного вида вывода решения, т.е
,
можно задать с помощью параметра
explicit=true. По
умолчанию действует параметр
explicit=false,
т.е. Maple будет выводить
решение в том виде, в каком «сочтет»
удобным. При указании explicit=true
он попытается записать его именно явно,
что видно из следующего примера
> dsolve(diff(y(x),x)/y(x)-ln(y(x))/(1+x^2)=0,
y(x));
> dsolve(diff(y(x),x)/y(x)-ln(y(x))/(1+x^2)=0,
y(x),explicit=true);
Решение также можно получить в виде степенного ряда (в Maple V не работает):
> dsolve(diff(diff(y(x),x),x)=4*diff(y(x),x)+y(x),
y(x),formal_series);
Нахождение частного решения
а) Решение задачи Коши для ОДУ
Пример.
Решить задачу Коши
,
,
.
> dsolve({diff(diff(y(x),x),x)-2*diff(y(x),x)+y(x)=sin(x),y(0)=1,D(y)(0)=0},y(x));
Отметим, что в последнем выводе не следует понимать y(x) ни как функцию, ни как переменную, хранящую решение уравнения. Другими словами, нельзя обращаться к y(x) как к обычной математической функции (равно как и к переменной). Например, Maple откажется выводить решение в какой-либо точке:
> y(2.2);
y(2.2)
или строить график этого решения
> plot(y(x),x=0..1);
Plotting error, empty plot
Выход может быть найден в использовании функции subs (подстановка). Например, вычертить график решения дифференциального уравнения можно, запуская сразу вслед за dsolve([…]) команду
> plot(subs(",y(x)),x=0..1);
Напомним, знак " означает подстановку последнего результата, вместо него можно ставить предварительно введенную переменную. Например,
> t:=dsolve({diff(diff(y(x),x),x)-2*diff(y(x),x)+y(x)=sin(x),y(0)=1,D(y)(0)=0},y(x)):
> plot(subs(t,y(x)),x=0..1);
Крайняя левая точка промежутка, на котором строится график, при решении задач Коши определяется по начальным условиям, правая точка – произвольно. В данном случае взято значение 1.
Если дальнейшие вычисления не ограничиваются построением графика решения уравнения, а требуют полноценной функции, то ее можно ввести через unapply. Разберите внимательно следующий фрагмент.
> t:=dsolve({diff(diff(y(x),x),x)-2*diff(y(x),x)+y(x)=sin(x),y(0)=1,D(y)(0)=0},y(x));
> u:=unapply(subs(t,y(x)),x); # теперь решение уравнения есть функция u(x)
> u(2.2); # значение этой функции при значении аргумента, равном 2.2
> plot(u(x),x=0..2); # график решения
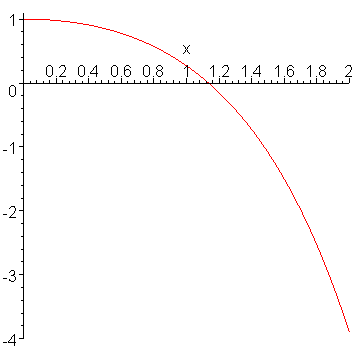
Табулирование функции u(x) на отрезке [0, 2] с шагом 0.2:
> for x from 0 by 0.2 to 2 do printf(`x=%g z=%g\n`,x,u(x)); od;
x=0 z=1
x=.2 z=.978594
x=.4 z=.908078
x=.6 z=.777092
x=.8 z=.570907
x=1.0 z=.270151
x=1.2 z=-.150833
x=1.4 z=-.726056
x=1.6 z=-1.500509
x=1.8 z=-2.53346
x=2.0 z=-3.902601
То же решение в виде разложения в степенной ряд по степеням x
> dsolve({diff(diff(y(x),x),x)-2*diff(y(x),x)+y(x)=sin(x),y(0)=1,D(y)(0)=0},y(x),series);
Максимальный порядок полинома, который выводит эта функция, определяется глобальной переменной Order. По умолчанию для этой переменной установлено значение 6. По желанию его можно поменять, например,
> Order:=10;
Если после этого запустить последнюю функцию, система выдаст 10 слагаемых ряда:
С параметром method=laplace решение осуществляется операционным методом – путем преобразования Лапласа. Для некоторых линейных уравнений (например, с разрывной правой частью) этот способ решения может оказаться предпочтительнее.
Пример.
Решить задачу Коши
,
,
.
> dsolve({diff(y(t),t$2)+5*diff(y(t),t)+6*y(t)=10*sin(t),
y(0)=0,D(y)(0)=1},y(t),method=laplace);
б) Решение краевой задачи для ОДУ
Пример.
Решить краевую задачу
,
,
.
> dsolve({diff(diff(y(x),x),x)-2*diff(y(x),x)+y(x)=sin(x),y(0)=1,y(1)=2},y(x));
Это краевая задача 1-го рода. Maple справляется и с задачей 2-го рода:
Пример.
Решить краевую задачу
,
,
> eqns:={diff(diff(y(x),x),x)+y(x)=1/(1+cos(x)),
D(y)(0)=1,D(y)(Pi/2)=1}:
> dsolve(eqns,y(x));
Данный пример показывает, что уравнение и дополнительные условия можно задать заранее, объявив вспомогательную переменную (в данном случае eqns).
Maple
V плохо справляется с
решением краевых задач 3-го года. Например,
краевую задачу
,
,
он не решает, хотя известно, что
аналитическое решение для неё существует.
Тем не менее, выход можно найти, если
сначала получить общее решение, содержащее
две произвольные постоянные, а затем
определить эти постоянные, удовлетворив
его граничным условиям. Приведенный
ниже фрагмент демонстрирует такую
возможность.
> eqns:=diff(diff(y(x),x),x)+y(x)=sin(x): # исходное уравнение
> bound:={D(y)(0)+2*y(0)=-1,D(y)(Pi/2)-y(Pi/2)=0};# граничные условия
t:=dsolve(eqns,y(x)); # получение общего решения
> y:=unapply(subs(t,y(x)),x);# задание функции y(x) для хранения общего решения
>r:=solve(bound,{_C1,_C2}); # нахождение произвольн. постоянных из системы двух уравнений
> subs(r,y(x));# подстановка найденных значений _C1 и _С2 в решение
Отметим, что Maple версии 7 и выше эту задачу решает через dsolve без проблем:
> eqns:={diff(diff(y(x),x),x)+y(x)=sin(x),D(y)(0)+2*y(0)=-1,D(y)(Pi/2)-y(Pi/2)=0}:
> dsolve(eqns,y(x));
