
- •Раскрытие неопределенностей в теории пределов
- •Введение
- •1. Понятие, определние и свойства предела функции
- •2. Бесконечно малые и бесконечно большие функции
- •3. Первый замечательный предел
- •4. Второй замечательный предел
- •5. Раскрытие неопределенностей вида
- •6. Раскрытие неопределенностей вида
- •7. Раскрытие неопределенности вида
- •8. Раскрытие неопределенности вида
- •9. Раскрытие неопределенности вида
- •10. Применение бесконечно малых к раскрытию неопределенностей
- •11. Раскрытие неопределЕнностей по правилу лопиталя
- •12. Некоторые специфические методы Раскрытия неопределЕнностей вида
- •Применение рядов к раскрытию неопределенностей
- •Библиографический список
- •Оглавление
- •Раскрытие неопределенностей в теории пределов
- •394006 Воронеж, ул. 20-летия Октября, 84
7. Раскрытие неопределенности вида
Этот вид неопределенности приводится
к виду
![]() или
с помощью тождественных преобразований.
или
с помощью тождественных преобразований.
Замечание. Неопределенности
вида
![]() и
и
![]() называют классическими.
называют классическими.
Примеры
Вычислить пределы:
1. Найти
![]() .
.
Умножим и разделим данное выражение на
сопряженное ему, т.е. на
![]() .
.
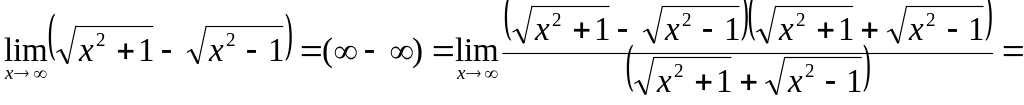
![]()

2.
![]() .
.
В этом случае достаточно привести дроби к общему знаменателю.
![]()
 .
.
8. Раскрытие неопределенности вида
Этот вид неопределенности тоже относится к классическим, если один из множителей опустить в знаменатель знаменателя, т.е. привести к "трехэтажной" дроби.
Например,

Примеры
Вычислить пределы:
1.
![]()

 (выделен первый замечательный предел).
(выделен первый замечательный предел).


3.
Найти:
![]() .
.
Полагая
![]() ,
получаем
,
получаем
![]()
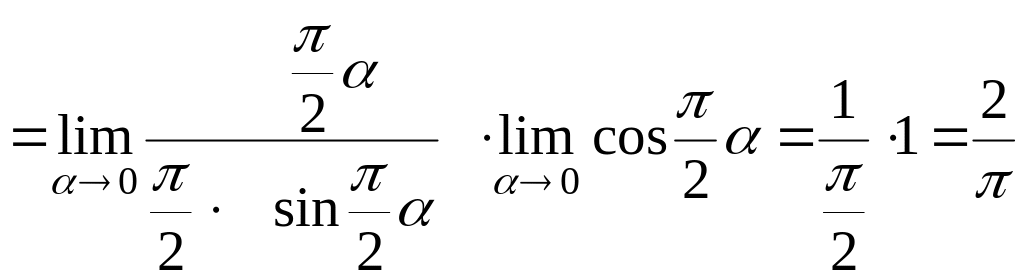

(выделен первый замечательный предел).
9. Раскрытие неопределенности вида
Такие
неопределенности возникают при вычислении
пределов степенно-показательных функций:
![]() ,
если
,
если
![]()
Неопределенности этого вида раскрывают при помощи второго замечательного предела, используя его в структурном виде (15).
 (17)
(17)
Пример 1
Найти

![]()
 ,
т.к. в рамке вы
,
т.к. в рамке вы
делен второй замечательный предел. В более сложных случаях удобно вводить замену переменной.
Пример 2
Найти
![]()
Имеем
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() и при
и при
![]() ,
,
![]()
![]() ,
,
Предел круглой скобки:
![]() .
.
Пример 3
Найти
![]() .
.
![]()
 (выделен второй замечательный предел,
учитывая, что если
(выделен второй замечательный предел,
учитывая, что если
![]() ,
то и
,
то и
![]() ).
).
Пример 4
Найти
![]()
Это неопределенность вида
![]() ,
т.к.
,
т.к.
![]() .
.
Д
ля
того чтобы раскрыть эту неопределенность,
представляем основание степени в виде
(1+![]() ),
а в показателе выделим множитель : :
),
а в показателе выделим множитель : :
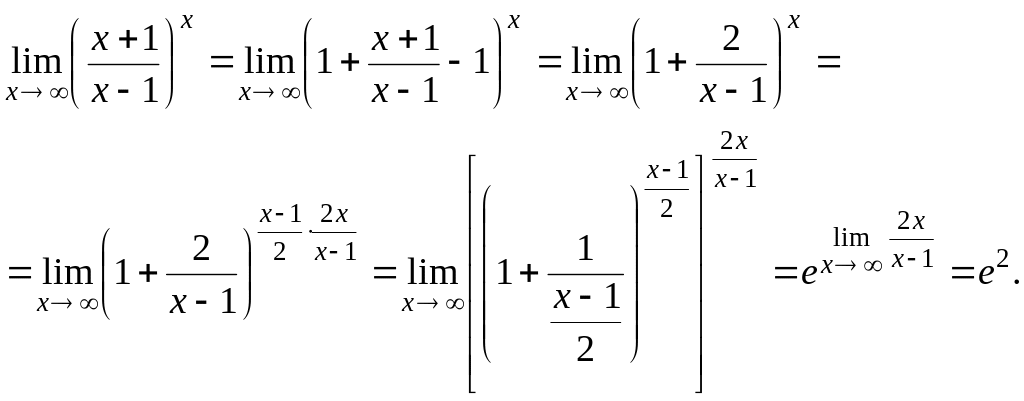

В рамке выделен второй замечательный
предел, т.к. если
![]() ,
то
,
то
![]() .
.
Рассмотрим несколько примеров, в которых для раскрытия неопределенностей применяются "важные пределы" (10–14).
Примеры
1. Вычислить
![]() .
.
Положим
![]() ,
,
![]() ,
,
тогда
![]()
![]() .
.
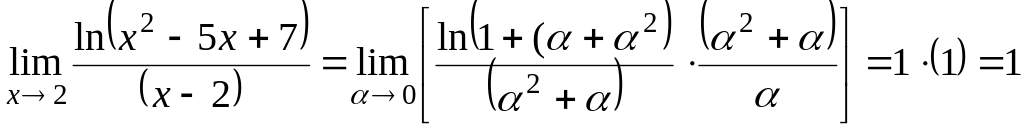 .
.
Использовали «важный предел» (11) в структурном виде
![]()

 .
.
2. Вычислить
![]()
![]() .
.
Применили предел (12): .
3. Вычислить
![]()
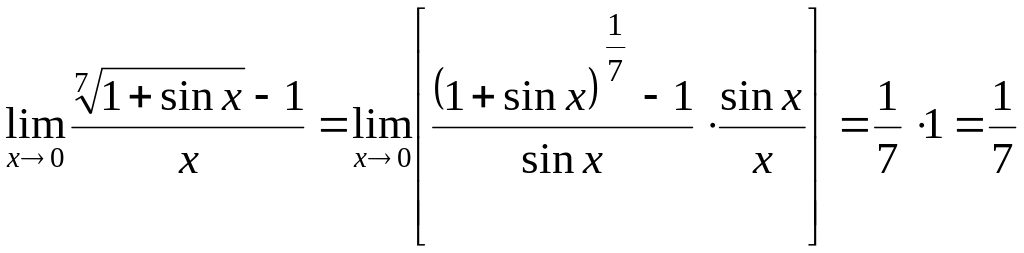
 .
.
П
рименили
предел (13) в структурном виде
![]() .
.
В рамке выделен первый замечательный предел.
10. Применение бесконечно малых к раскрытию неопределенностей
Функция
![]() называется бесконечно малой функцией
[1, 3, 11], если ее предел равен нулю, т.е.
называется бесконечно малой функцией
[1, 3, 11], если ее предел равен нулю, т.е.![]() или пишут
или пишут
![]() .
.
Но бесконечно малые функции могут стремиться к нулю по-разному: одни – быстрее, другие – медленнее. Для сравнения бесконечно малых функций вычисляют предел их отношения.
Говорят,
что бесконечно малые функции
![]() и
и
![]() называются бесконечно малыми одного
порядка малости, если предел их отношения
равен некоторому числу
называются бесконечно малыми одного
порядка малости, если предел их отношения
равен некоторому числу
![]() ,
отличному от нуля, т.е.
,
отличному от нуля, т.е.
![]() .
(18)
.
(18)
Пример
Найдем
![]() ,
следовательно, sin7
и
являются бесконечно малыми одинакового
(одного) порядка малости.
,
следовательно, sin7
и
являются бесконечно малыми одинакового
(одного) порядка малости.
Если
же
![]() ,
т.е.
,
т.е.
![]() ,
то бесконечно малая
называется бесконечно малой более
высокого порядка по сравнению с
или бесконечно малая
,
то бесконечно малая
называется бесконечно малой более
высокого порядка по сравнению с
или бесконечно малая
![]() называется бесконечно малой меньшего
порядка малости по сравнению с
называется бесконечно малой меньшего
порядка малости по сравнению с
![]() .
.
В
этом случае используют условное
обозначение:
![]() при
при
![]() и читают:
и читают:
![]() есть
«о» малое от
при
.
есть
«о» малое от
при
.
Пример
Найдем
![]() ,
следовательно,
,
следовательно,
![]() есть бесконечно малая более высокого
порядка малости, чем
есть бесконечно малая более высокого
порядка малости, чем
![]() (
(![]() стремится к нулю быстрее, чем
стремится к нулю быстрее, чем
![]() ).
).
Бесконечно
малые функции
и
называются эквивалентными
(равносильными),
если
![]() .
Эквивалентные бесконечно малые обозначают
так:
.
Эквивалентные бесконечно малые обозначают
так:
![]() .
(19)
.
(19)
Пример
Так
как
![]() ,
то
,
то
![]() и
и
![]() – эквивалентные бесконечно малые
функции:
~
.
– эквивалентные бесконечно малые
функции:
~
.
Из определения следует, что эквивалентные бесконечно малые функции имеют одинаковый порядок малости.
Равенство отношений двух бесконечно малых и эквивалентных им функций следует из следующей теоремы
Теорема
Если
![]()
![]() ,
,
![]()
![]() при
при
![]() и существует
и существует
![]() ,
то существует
,
то существует
![]() ,
причем
,
причем
= . (20)
Кратко эта теорема формулируется следующим образом: предел отношения двух бесконечно малых функций равен пределу отношения эквивалентных им функций.
Эта теорема позволяет во многих случаях упрощать отыскание пределов (раскрывать неопределенности). Смысл этого метода заключается в том, что, заменяя отношения данных функций отношением эквивалентных им функций, пределы этих отношений не изменяются, но вместо неопределенности получаем сразу конечный (или бесконечный) предел.
Замечание.
Все рассуждения и формулы верны для
любых предельных значений:
,
![]() ,
,
![]() ,
.
,
.
Легко
установить эквивалентность следующих
функций при
![]() :
:
 (21)
(21)
Примеры
С помощью эквивалентных бесконечно малых найти пределы.
1.
Найти
![]() .
.
Решение
Имеем неопределенность вида .
При
![]() функция
функция
![]() бесконечно малая и
бесконечно малая и
![]() ,
т.к.
,
т.к.
![]()
Заменяя
![]() эквивалентной ей
эквивалентной ей
![]() ,
получаем
,
получаем

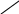 .
.
Найти
 .
.
Решение
Так
как
![]() ,
то заменяя в числителе данную бесконечно
малую ей эквивалентной, получим
,
то заменяя в числителе данную бесконечно
малую ей эквивалентной, получим
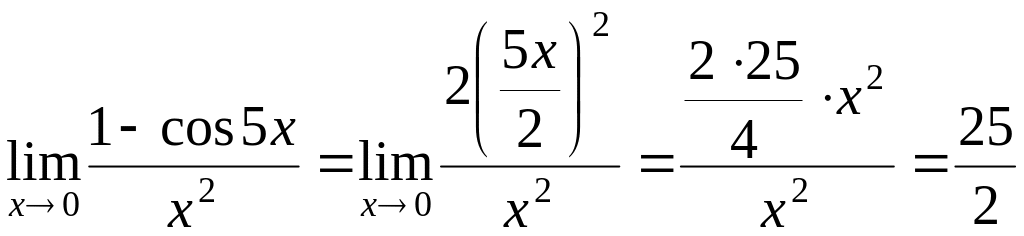
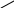
 .
.
3.
Найти
![]() .
.
Решение
Так
как
![]() ,
то
,
то
![]() .
.
При
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поэтому, заменяя данные функции на эквивалентные, получаем
![]() .
.
4.
Найти
 .
.
Решение
Поскольку
![]() ,
а (
,
а (![]() ,
,
то
 .
.
5.
Найти
![]() .
.
Решение. Преобразуем числитель и знаменатель, а потом заменим эквивалентными.
Так
как
![]() ,
,
![]() ,
то
,
то
![]() ,
т.к.
,
т.к.
![]() .
.
Получим
 .
.
6.
Найти
![]() .
.
Решение
Так
как
![]() ,
,
то
 .
.
Но
при
![]() функция (
функция (![]() )
– бесконечно малая, тогда
)
– бесконечно малая, тогда
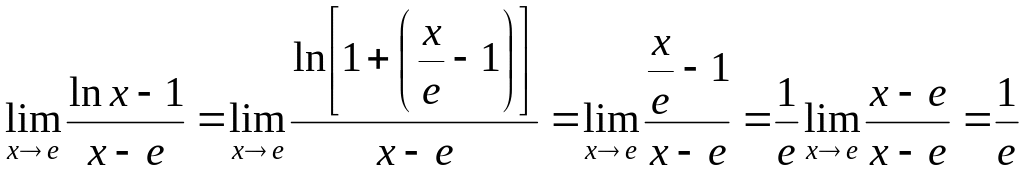 .
.
Замечание.
Если
![]()
![]() ,
то в ряде случаев удобно сначала ввести
бесконечно малую функцию
,
то в ряде случаев удобно сначала ввести
бесконечно малую функцию
![]() (или
(или
![]() ).
).
Пример
Найти
![]() .
.
Решение
Здесь числитель и знаменатель функции бесконечно малые.
Однако
х
не является бесконечно малой функцией
(стремится не к нулю, а к ),
поэтому соотношение
![]() не имеет смысла.
не имеет смысла.
Введем
бесконечно малую
![]() ,
тогда
,
тогда
![]()
и
![]() .
.
Найти
![]() .
.
Это
неопределенность вида
![]() .
.
Сделаем
предварительно замену переменной. Если
ввести обозначение
![]() ,
то
,
то
![]() при
при
![]() ,
тогда
,
тогда
![]()
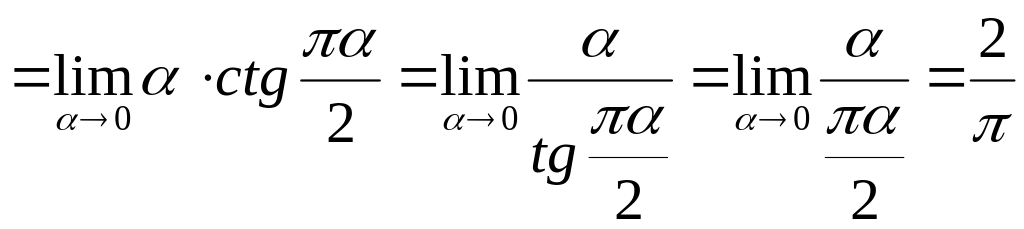 .
.
Замечание.
При вычислении пределов выражений вида
![]() ,
где
,
где
![]() ,
а
,
а
![]() (неопределенность вида (
(неопределенность вида (![]() ),
удобно применить формулу (4):
),
удобно применить формулу (4):
![]() .
(22)
.
(22)
Эта формула следует из свойств логарифмов:
![]() .
.
Примеры
1.
Найти
![]() .
.
Так
как при
,
![]() и
и
![]() ,
пользуясь формулой (10), получим
,
пользуясь формулой (10), получим
![]() .
.
2.
Найти
![]()
![]()
=![]() .
.
Найти
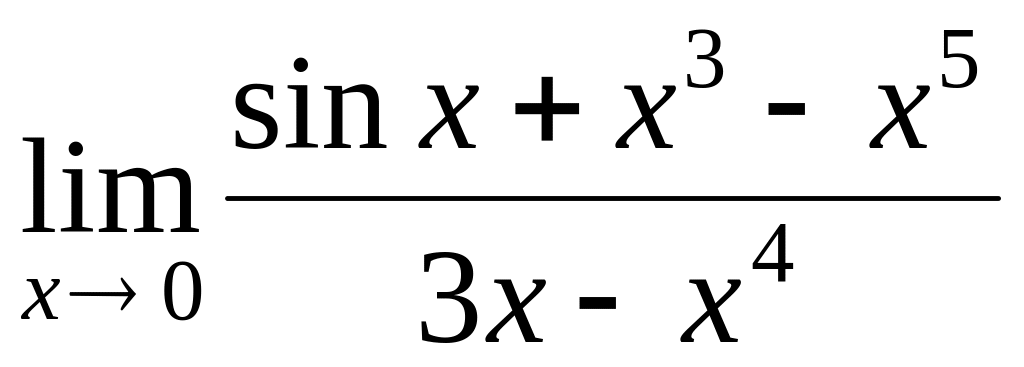 .
.
При
![]() ,
т.к. разность
,
т.к. разность
![]() бесконечно малая функция более высокого
порядка по сравнению с
бесконечно малая функция более высокого
порядка по сравнению с
![]() и с
и с
![]() .
.
Аналогично
![]() .
.
Поэтому
![]() .
.
