1.2. Основные типы задач и методы их решения Классификация

1. Нахождение траектории движения материальной точки, ее скорости и ускорения в различные моменты времени на основании кинематических уравнений движения.

Метод решения. Последовательное дифференцирование кинематических уравнений движения в координатной форме. Использование соотношений, определяющих векторы скорости и ускорения, их модули.

2. Нахождение пути, пройденного материальной точкой на основании закона изменения ее скорости или ускорения с течением времени.

Метод решения. Прямое интегрирование выражений

, .

3. Движение тела, брошенного под углом к горизонту. Нахождение траектории движения, ее кривизны в различных точках, высоты, дальности и продолжительности полета.

Метод решения. Составление уравнений движения вдоль соответствующих координатных осей на основании начальных условий и непосредственное их решение. Использование соотношений, определяющих тангенциальную и нормальную составляющую ускорения.

4. Вращение тела вокруг неподвижной оси. Нахождение угловой скорости и углового ускорения, числа оборотов за определенный промежуток времени; полного, нормального и тангенциального ускорений точек тела.

Метод решения. Применение формул, определяющих угловую скорость и угловое ускорение, и соотношений, связывающих линейные и угловые величины. Использование аналогии между поступательным и вращательным движениями.

Примеры

I тип задач. Движение частицы в плоскости описывается уравнениями , , где А и В – константы. Определить: 1) уравнение траектории ; 2) векторы скорости, ускорения и их численные значения; 3) вектор средней скорости за первые секунд и его модуль.

Решение

1) Для нахождения уравнения траектории движения частицы необходимо исключить параметр t из кинематических уравнений:

.

Полученное уравнение описывает параболу.

2) Вектор скорости частицы в момент времени t определяется выражением

.

Дифференцируя уравнения (1) по времени, получим

, (1)

и, следовательно, .

Модуль вектора скорости равен

.

Вектор ускорения определяется выражением

,

в котором составляющие ускорения могут быть найдены дифференцированием (1):

, .

Следовательно, .

Знак “минус” в полученном выражении свидетельствует о том, что ускорение направлено в сторону, противоположную оси У.

Модуль вектора ускорения равен .

3) Вектор средней скорости за первые секунд дается выражением

,

где , поскольку t₀ = 0. Находим

, .

Окончательно ,

.

II тип задач. Частица движется со скоростью , где А – константа. Найти путь S, пройденный частицей с момента t₁ до момента t₂.

Решение

Путь, пройденный частицей за определенный промежуток времени, равен интегралу от функции , в пределах от t₁ до t₂: . Модуль скорости определяется выражением , в котором проекции вектора скорости на координатные оси равны , , .

Следовательно,

и .

III тип задач. Тело брошено под углом к горизонту с начальной скоростью . Найти, пренебрегая сопротивлением воздуха: 1) максимальную высоту подъема; 2) максимальную дальность полета; 3) радиус кривизны траектории в начальный момент времени.

Решение

1

Рис. 1.1

) В данной задаче рассматривается плоское криволинейное движение материальной точки, для описания которого достаточно взять прямоугольную систему координат ХОУ. Начало отсчета удобно выбрать в точке бросания (рис. 1.1).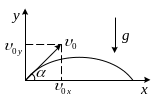

Сложное криволинейное движение можно рассматривать как совокупность двух прямолинейных движений. Движение вдоль оси ОХ равномерное (а_х = 0) с начальной скоростью , движение вдоль оси ОУ неравномерное ( ) с начальной скоростью . Законы изменения проекций скорости и со временем выражаются соотношениями

, (1)

. (2)

Кинематические уравнения движения имеют вид

, (3)

. (4)

Полученная система уравнений (3)-(4) позволяет определить искомые величины.

Учитывая, что в верхней точке траектории , время подъема t₁ определяется из уравнения (2): ,

Откуда

. (5)

Подставляя (5) в уравнение (4), получаем

.

2) Для определения максимальной дальности полета необходимо, прежде всего, найти время полета t₂. Последнее может быть определено из уравнения (4), решение которого для у = 0 имеет два значения t₁ = 0, . Первое решение соответствует началу движения, второе – его окончанию, т.е. времени полета частицы. Возможно также нахождение t₂ более простым способом. В силу симметрии траектории движение частицы

.

Дальность полета найдем, подставив t₂ в уравнение (3):

.

Из полученного результата видно, что дальность полета максимальна при , т.е. для . Более того, х_max сохраняет свое значение при замене на , т.е. дальность полета одинакова при двух дополнительных углах бросания.

3

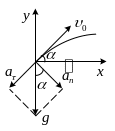Рис. 1.2

) В соответствии с формулой радиус кривизны траектории в любой точке можно определить, зная нормальное ускорение и скорость в данной точке. В момент времени t = 0, .

Разлагая вектор полного ускорения частицы на две составляющие (рис. 1.2), получим . Следовательно, .