5.4. Построение комбинационной логической схемы по заданной функции. Минимизация логических функций

Все логические элементы можно разделить на два класса — собственно логические элементы и элементы памяти. В зависимости от класса используемых элементов различают комбинационные логические устройства, в которые входят только логические элементы, и последовательностные логические устройства, которые кроме логических элементов содержат еще и элементы памяти. В комбинационных логических устройствах выходной сигнал зависит только от значений входных сигналов в рассматриваемый момент времени, а в последовательностных логических устройствах — от значений входных сигналов в рассматриваемый момент времени и от выходных сигналов элементов памяти, которые являются результатом логической обработки сигналов, поступивших в предшествующие моменты времени. Мы рассмотрим здесь построение только комбинационных логических схем.

Перед проектированием логической схемы в цифровых устройствах бывает задана таблица переключений — таблица истинности устройства, в которой даны входные сигналы и соответствующие каждому сочетанию входных сигналов выходные сигналы. Первый этап проектирования состоит в отыскании такой логической функции, которая соответствует таблице истинности устройств. При этом поступают следующим образом.

1. В таблице истинности выделяют строки, в которых выходная переменная y имеет значение 1.

2. Для каждой такой строки составляют произведение всех входных логических переменных, записывая сомножитель x_i, если рассматриваемая переменная имеет значение 1, и сомножитель , если эта переменная имеет значение 0.

3. Получив столько произведений, сколько имеется строк с y=1, записывают логическую функцию устройства в виде суммы всех найденных произведений. Такую форму записи искомой функции называют совершенной дизъюнктивной нормальной формой (СДНФ), т. е. дизъюнкцией конъюнктивных членов одинаковой размерности.

Дальнейшие действия зависят от средств реализации функций, к которым в настоящее время относят:

логические блоки табличного типа (программируемые БИС/СБИС на основе схем программируемой памяти);

логические блоки в виде последовательности матриц элементов И и ИЛИ (ПЛМ — программируемая логическая матрица для реализации системы переключательных функций, представленных в ДНФ и составляемых из единого набора коньюнктивных термов; ПМЛ — программируемая матричная логика для реализации системы переключательных функций, представленных в ДНФ, каждая из которых составляется из индивидуального набора относительно небольшого числа коньюнктивных термов);

универсальные логические блоки в виде мультиплексоров — схем, передающих на выход одну из нескольких входных величин под управлением адресующего кода;

логические блоки, собираемые из логических элементов некоторого базиса.

Для реализации комбинационной схемы на основе логического блока табличного типа СДНФ является окончательным видом функции и никаких дальнейших преобразований этой функции не требуется, поскольку табличный блок представляет собой память, в которой имеется столько ячеек, сколько необходимо для хранения всех значений функции, т. е. 2^m, где m — число аргументов функции. Набор аргументом является адресом той ячейки, в которой хранится значение функции на этом наборе (0 или 1). СДНФ как раз и содержит все адреса, по которым нужно хранить единичные значения функции. Если искомая функция выражена в какой-либо сокращенной форме, то следует перевести ее в СДНФ. Для этого коньюнктивные члены, не содержащие переменной x_i, умножают на равную 1 дизъюнкцию . Например,

а) б)

Рис. 5.16. Блоки памяти для воспроизведения одной (а) и нескольких (б) логических функций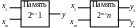

Блок памяти для воспроизведения функции m переменных имеет вид рис. 5.16, а. Если требуется воспроизвести n функций, то в каждой ячейке нужно хранить n бит (по одному биту для каждой функции), и блок памяти будет организован, как показано на рис. 5.16, б.

При необходимости перехода к заданному логическому базису проводят минимизацию логической функции в смысле упрощения ее по заданному критерию. Целью минимизации является сокращение числа коньюнктивных термов в данной системе функций, т. е. поиск кратчайших дизъюнктивных форм. Практически это сводится к поиску минимальных форм дизъюнктивных нормальных форм (ДНФ) и отбору среди них вариантов с достаточно малым числом термов. Исторически первым было стремление минимизировать число логических элементов (корпусов ИС) в схеме.

Таблица 5.6

Таблица истинности мажоритарного элемента

Строка	x1	x2	x3	y	Выходная логическая функция
1	0	0	0	0	—
2	0	0	1	0	—
3	0	1	0	0	—
4	0	1	1	1
5	1	0	0	0	—
6	1	0	1	1
7	1	1	0	1
8	1	1	1	1

Рассмотрим способ нахождения логической функции на примере таблицы истинности 5.6.

В строках 4, 6, 7, 8 выходная переменная y=1. Соответствующие произведения для этих строк будут: ; ; ; . Искомая логическая функция

Если в таблице истинности в столбце выходной переменной y стоит много единиц, требуется составить большое число произведений, что неудобно. Поэтому при числе нулей меньшем числа единиц составляют логическую функцию для переменной .

Для создания логического устройства, выполняющего обработку сигналов x₁, x₂, x₃ в соответствии с полученной логической функцией, нужны все три типа логических элементов: НЕ, ИЛИ и И. Для выполнения инверсий сигналов x₁, x₂, x₃ требуется три элемента НЕ. Затем нужно четыре элемента И, которые обеспечат операцию конъюнкции каждого слагаемого (называемого в булевой алгебре минтермом), и один логический элемент ИЛИ на четыре входа, который осуществляет операцию логического суммирования всех минтермов. В результате логическая схема мажоритарного элемента примет вид, показанный на рис. 5.17, а.

а) б)

Рис. 5.17. Цифровые схемы мажоритарного элемента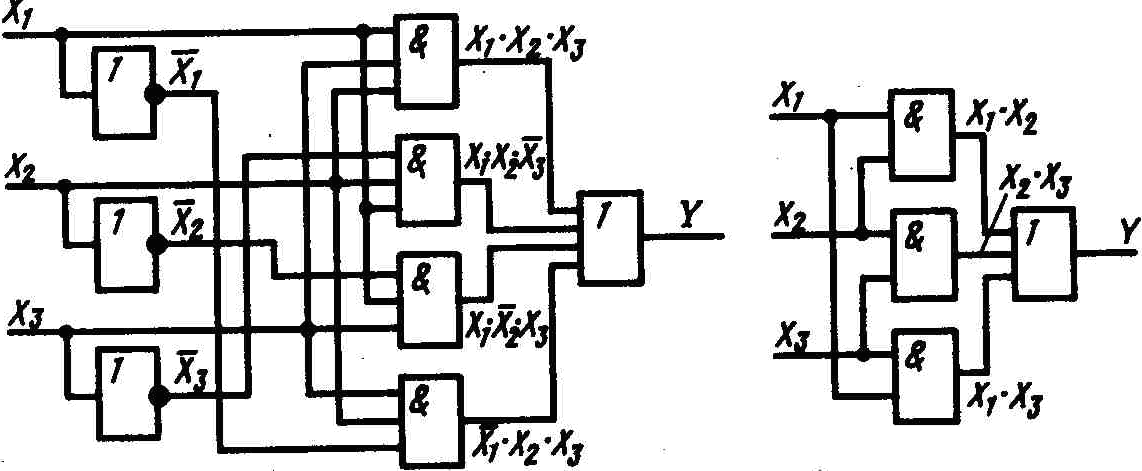

Первый путь минимизации, называемый алгебраическим, состоит в последовательном применении законов алгебры логики для сокращения избыточных членов в первоначальной логической функции.

В качестве примера минимизируем полученную в рассмотренном примере функцию. Для этого сначала добавим еще два таких же слагаемых, как последнее. Это в соответствии с законом тавтологии не изменит функцию. Тогда получим

Затем воспользуемся распределительным законом и произведем следующую группировку членов:

Так как (закон дополнительности), то окончательно имеем

что может быть реализовано гораздо проще (рис. 5.17, б).

Минимизация логических функций алгебраическим методом требует определенных навыков. При большом числе аргументов и большом числе слагаемых логические формулы получаются труднообозримыми и их преобразование затруднительно. В таких случаях применяют специальные способы, позволяющие как бы «автоматизировать» процедуру минимизации. Один из таких способов связан с применением карт Карно — таблиц, разбитых на ячейки, в которых помещаются наборы всех минтермов (логических произведений переменных — их прямых и инверсных значений) данной логической функции, расположенных в таком порядке, что соседние минтермы можно «склеить». Поэтому первый этап сводится просто к систематическому расположению всех минтермов, входящих в минимизируемую сложную логическую функцию. После этого «соседние» минтермы преобразуются, в результате чего они сокращаются на одну или две единицы. Для пояснения работы с картами Карно минимизируем с их помощью полученную из табл. 5.6 функцию.

Рис. 5.18. Карта Карно для функций трех аргументов (а) и операция «склеивания» (б)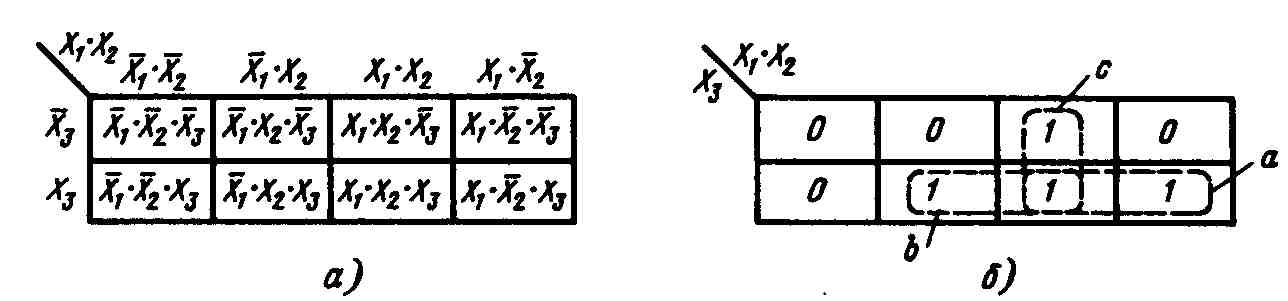

Карта Карно для функций трех аргументов показана на рис. 5.18, а. Все минтермы минимизируемой функции отметим в соответствующих ячейках карты Карно в виде 1, в остальных ячейках поставим 0 (рис. 5.18, б). «Склеивание» осуществляется между теми минтермами, которые записаны в виде 1 в соседних ячейках. Соседними считаются ячейки как по вертикали, так и по горизонтали, а также ячейки верхнего и нижнего ряда карты и ячейки крайнего левого и крайнего правого ряда (карту Карно следует представлять в виде развертки цилиндра, ось которого следует принимать либо вертикальной, либо горизонтальной). В рассматриваемом случае соседними оказались минтермы, объединенные контурами a, b и c.

Рис. 5.19. Карты Карно для функций двух, трех, четырех и пяти аргументов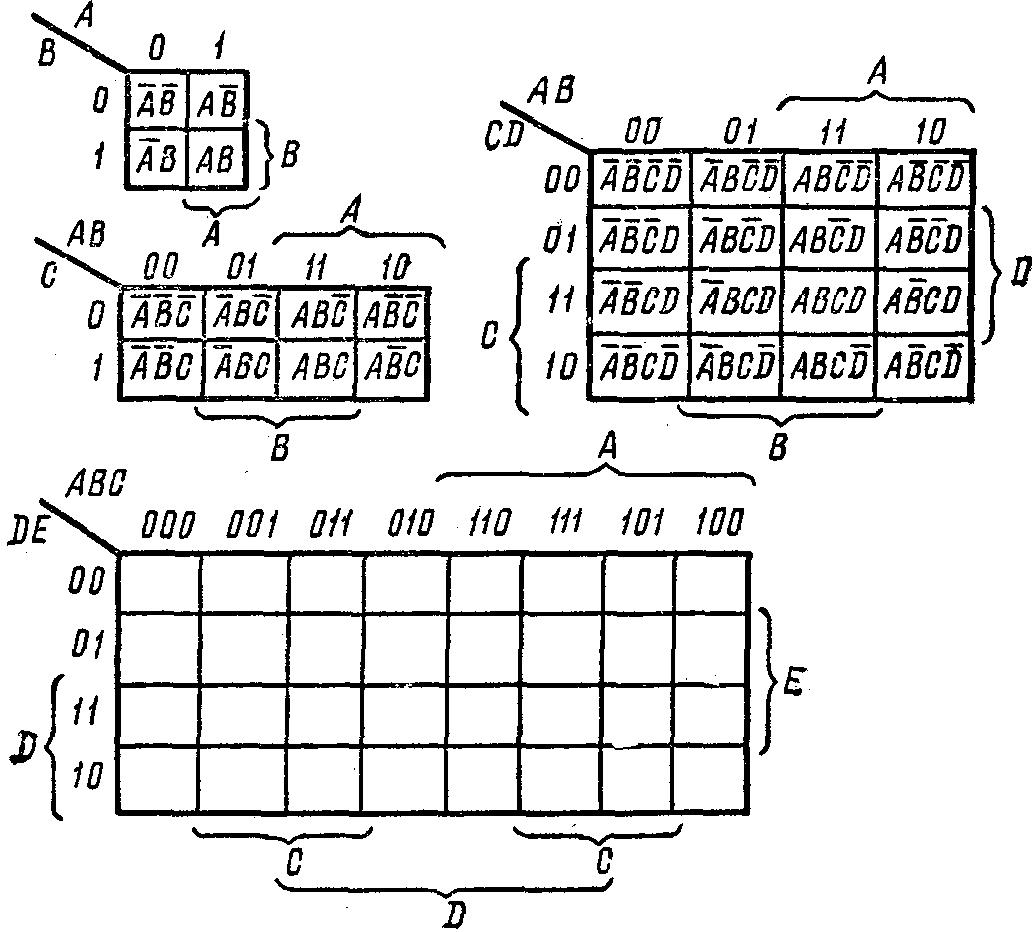

Объединение, соответствующее контуру a, позволяет провести следующее «склеивание»:

Объединение, соответствующее контуру b, — «склеивание»:

Объединение, соответствующее контуру с, — «склеивание»:

В результате применения карты Карно получаем

что совпадает с результатом, полученным ранее, но сейчас это удалось сделать быстрее и удобнее.

При минимизации можно склеивать и соседние минтермы, отмеченные 0, сумма которых дает функцию . Иногда этим свойством булевых функций оказывается целесообразно воспользоваться, так как, имея логическую функцию , легко построить функцию y, добавив один элемент НЕ на выходе. Так поступают в тех случаях, когда число логических элементов для реализации функции оказывается меньше, чем для функции y.

Правила перехода от исходных выражений к заданному логическому базису основаны на применении теоремы де Моргана. В частности, для перехода к базису И–НЕ используется соотношение

а для перехода к базису Пирса удобно вначале получить исходную булевскую форму для инверсии искомой функции, а затем перейти к базису ИЛИ–НЕ по соотношениям

Карты Карно для функции двух—пяти аргументов приведены на рис. 5.19.