3.4 Комбинированный проблемно – адаптивный алгоритм оптимизации обобщенных критериев оптимальности уцос

В процессе решения задачи оптимизации (3.1) возникает большое количество не предсказуемых заранее ситуаций. Предсказать эти ситуации на этапе разработки алгоритма оптимизации практически невозможно из за различного субъективного отношения пользователей к способам выхода из этих ситуаций. Совокупность таких ситуаций порождает задачу, относящуюся к трудно формализуемым. Построить жесткий алгоритм решения задачи (3.1) невозможно. Наиболее эффективным средством решения трудно формализуемых задач являются методы и программы искусственного интеллекта (ИИ), в частности экспертные системы (ЭС). Подходы, используемые в ИИ, позволяют легко учитывать эвристические знания проектировщиков, накопленные ими при решении большого числа практических задач. Однако стандартные ЭС содержат в своем составе большое количество сложных блоков, таких, например, как блок отбора знаний от экспертов, объясняющий блок и т. д. Быстродействие таких ЭС невелико. В то же время в процессе оптимизации требуется принимать решение либо достаточно быстро, либо оперативно (сверхбыстро). Следовательно, стандартная ЭС для принятия решений в этих случаях не годится.

Одним из путей построения гибких алгоритмов оптимизации УЦОС может служить проблемно – адаптивный подход, который неоднократно использовался целым рядом автором при решении разноплановых задач оптимального проектирования [32, 60, 75, 81, 97]. Этот подход достаточно целесообразен при построении комбинированных алгоритмов оптимизации УЦОС, так как предполагает наличие коллектива конкурирующих алгоритмов оптимизации, с помощью комбинирования которых можно строить гибкие стратегии оптимизации.

В коллектив оптимизирующих алгоритмов вошли: алгоритм поискового метода (ПМ), использующий ЛПτ-последовательности; алгоритм метода статистического градиента; алгоритм метода деформируемого многогранника; алгоритм метода сопряженных градиентов; модифицированный алгоритм метода ВН; алгоритм метода ВМ; модифицированный второй алгоритм Е.Я. Ремеза.

На основании результатов качественного исследования методов решения задачи (3.1) и (3.24), а также на основании опыта решения практических задач оптимизации можно предложить комбинированный проблемноадаптивный алгоритм оптимизации обобщенных критериев оптимальности при оптимальном проектировании УЦОС.

Процедура минимизации с использованием комбинированного проблемно -адаптивного алгоритма включает в себя четыре этапа, приведенные на рис. 3.3.

1. Анализ исходной точки с использованием алгоритма ПМ. Осуществляется минимизация среднеквадратичного обобщенного критерия . Алгоритм работает в соответствии с описанием, приведенным в п. 3.1. Процесс изменения размеров области поиска продолжается до тех пор, пока либо ее размеры не превысят размеров области допустимых значений (ОДЗ), либо пока диаметр гиперпараллелепипеда, образованного параметрическими ограничениями, не станет меньше требуемой точности вычислений. Результат первого этапа - опорное решение, которое используется на втором этапе.

2. Спуск по статистическому градиенту. Спуск по статистическому градиенту осуществляется по следующей схеме:

а) в точке X^(k) рассчитывается направление статистического градиента

G^(k) = grad Q^(k) / , где grad Q^(k) = - , где l=1,2, ..., L , - независимые случайные векторы, равномерно распределенные на сфере заданного радиуса вокруг точки X^(k); L – число пробных вычислений целевой функции.

б) рассчитывается значение целевой функции в точке

X₁^(k+1) = X₀^(k) + _k G^(k).

Если  , то есть точка неудачная, то этап заканчивается и происходит переход к третьему этапу минимизации. В противном случае (  ) рассчитывается также значение функции в точке X₂^(k+1) = X₀^(k) + 2_k G^(k). Если  , то в качестве следующей точки принимается точка , шаг _k остается прежним и процесс повторяется, начиная с пункта а). Если < , то = , =2 и процесс повторяется с пункта а).

Начальное значение шага ₀ принимается равным диаметру гиперпараллелепипеда, при котором закончился первый этап.

3. Минимизация среднестепенного критерия методом деформируемого многогранника.

Начальный размер многогранника определяется достигнутым на предыдущем этапе шагом поиска. В качестве начальной точки берется последняя успешная точка, полученная в процессе поиска по статистическому градиенту. Точность поиска задается пользователем. Стандартный алгоритм деформируемого многогранника модифицирован путем введения порога аналогично тому, как это сделано в алгоритме ПМ в п. 3.1. Для случая, когда производные конкретного обобщенного критерия вычисляются аналитически, а размерность вектора X относительно невелика, вместо метода деформируемого многогранника используется метод сопряженных градиентов, алгоритм которого приведен в п. 3.2.

Результат третьего этапа - опорное решение, которое используется на четвертом шаге.

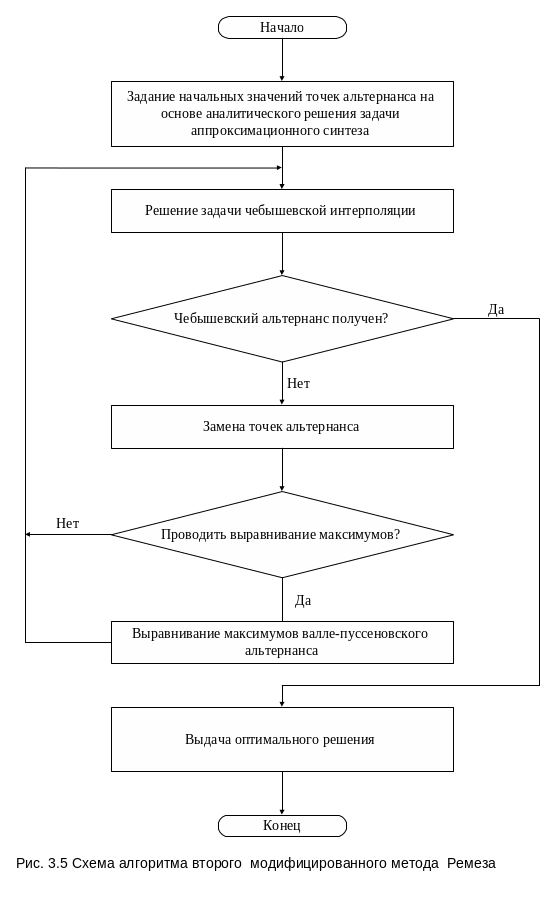
4. Минимизация минимаксного критерия. Опорное решение, полученное на третьем этапе, оптимизируется либо с использованием алгоритма метода ВМ, либо - ВН. Алгоритм метода ВМ используется в том случае, если на третьем этапе найден валле-пуссеновский альтернанс, в противном случае используется алгоритм метода ВН. Если минимаксный критерий линейный, то на третьем этапе используется модифицированный алгоритм Ремеза.

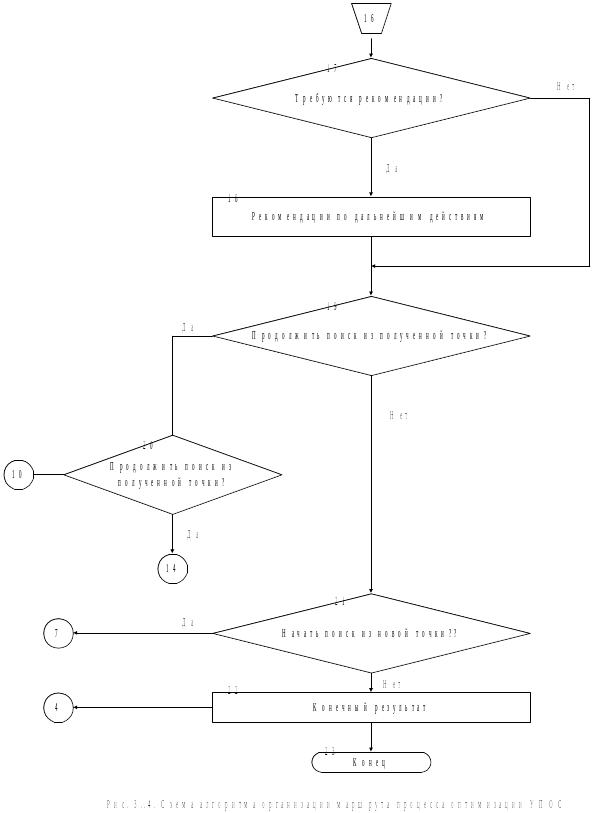
Общая схема маршрута проектирования приведена на рис. 3.4.

Структурная схема алгоритма Ремеза приведена на рис. 3.5.

Весовые коэффициенты (см. рис. 3.6) в свертке либо задаются пользователем, либо вычислены на основе комбинированного алгоритма, включающего в себя три известных метода: вычисления весовых коэффициентов по коэффициентам относительного разброса ЛКО, на основе теоретико-игровой модели и “энтропийной” модели. В ряде случаев расчет весовых коэффициентов производится путем решения задачи линейного программирования. Кроме того для расчета весовых коэффициентов использован метод зондирования пространства векторов весовых коэффициентов, основанный на построении ЛП - последовательностей.

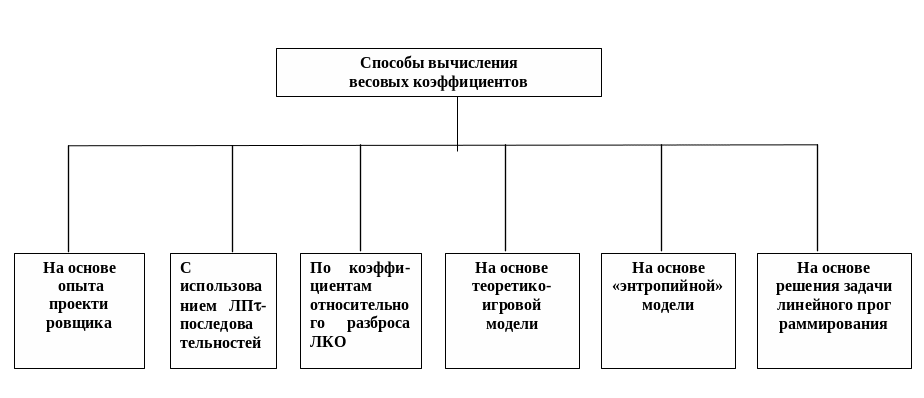Рис. 3.6 Методы вычисления весовых коэффициентов