Криволинейный интеграл 2-го рода

1. Задача, приводящая к понятию криволинейного интеграла 2-го рода.

Предположим, что при движении по кривой материальная точка переходит из точки в точку под воздействием силы , заданной своими проекциями на координатные оси:

.

Найдем работу силы по перемещению точки из в .

Если перемещение прямолинейно, а действующая сила постоянна по величине и направлению, то работа вычисляется по формуле .

Пусть перемещение криволинейное, а действующая сила переменная.

Разобьем кривую на дуг точками и обозначим диаметр разбиения (длину наибольшей дуги) через

(рис.22). На каждой частичной дуге выберем точку . Будем считать, что сила

с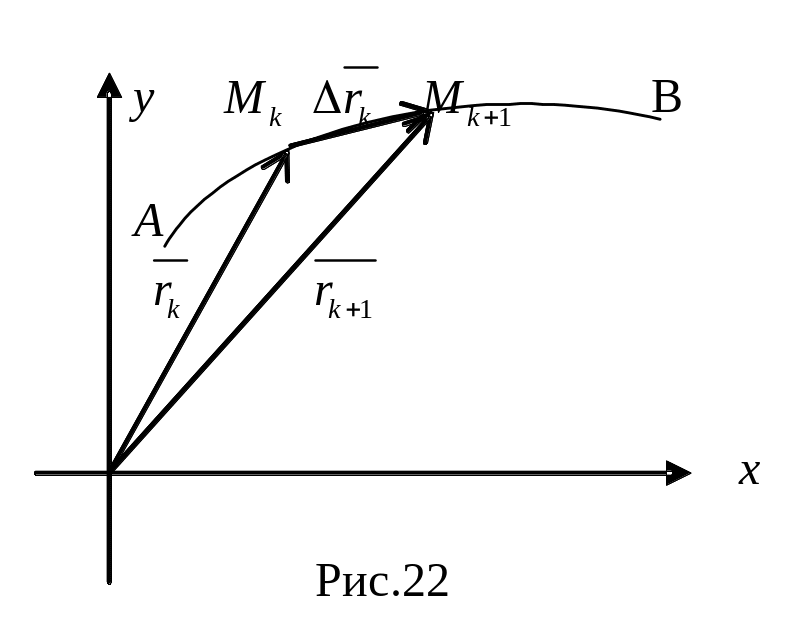 охраняется постоянной в точках дуги на малом участке и под ее воздействием точка перемещается по хорде

этой дуги. Тогда приближенное значение работы на каждой частичной дуге имеет вид

.

Суммируя элементарные работы, получаем

За работу силы по перемещению точки из в вдоль кривой примем предел суммы , то есть

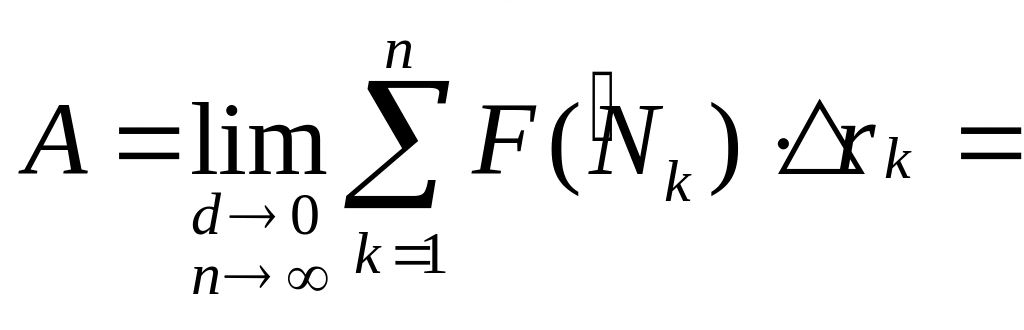
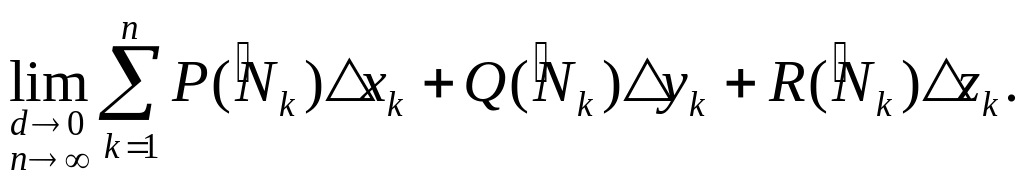
2. Определение криволинейного интеграла 2-го рода.

Рассмотрим теперь направленную кусочно-гладкую кривую

, заданную в . Дуга кривой называется гладкой, если задающие ее функции непрерывно дифференцируемы, и кусочно-гладкой, если ее можно разбить на конечное число гладких дуг. Пусть - векторное поле, определенное в некоторой области , содержащей дугу , функции непрерывны на кусочно-гладкой кривой . Разобьем кривую на дуг точками в направлении от до . На каждой частичной дуге выберем произвольную точку и составим сумму вида

Определение. Если существует предел последовательности интегральных сумм не зависящий ни от способа разбиения кривой на части, ни от выбора точек , то он называется криволинейным интегралом второго рода (по координатам) и

обозначается 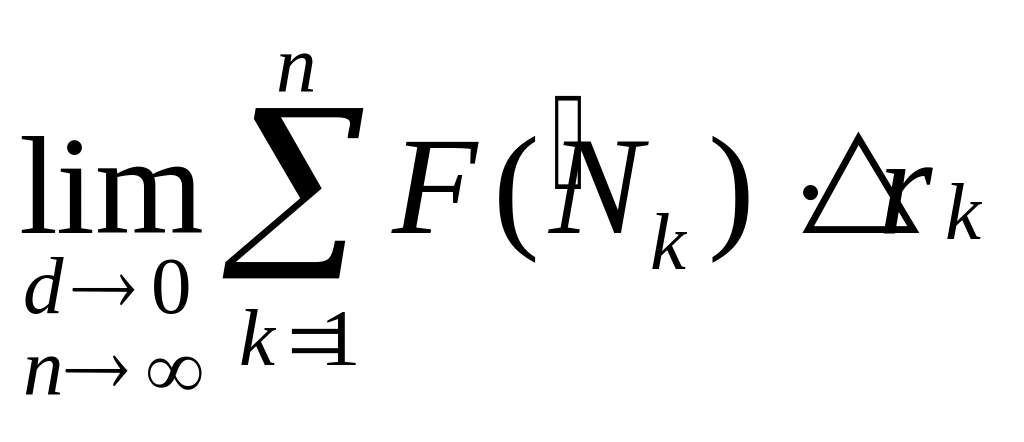, то есть

,

где

Сравнивая формулы для определения работы и определение криволинейного интеграла заключаем, что . Таким образом, криволинейный интеграл 2-го рода выражает работу силы по перемещению точки из в вдоль кривой . В этом состоит физический смысл криволинейного интеграла 2-го рода.

3. Свойства криволинейного интеграла 2-го рода

1.При изменении направления интегрирования криволинейный интеграл изменяет свой знак , то есть

2.Если путь интегрирования разбит на непересекающиеся части (рис.23), то криволинейный интеграл вдоль всего пути равен сумме криволинейных интегралов вдоль его частей

3. Постоянный множитель можно выносить за знак криволинейного интеграла.

4. Криволинейный интеграл от суммы равен сумме криволинейных интегралов.

Все свойства непосредственно следуют из определения криволинейного интеграла.

Замечание. Для криволинейных интегралов второго рода

теорема об оценке модуля интеграла и формула среднего значения неверны.

Пусть - замкнутая кривая (замкнутый контур), то есть точка совпадает с точкой , тогда для нее можно указать два направления обхода от к . Если область, лежащая внутри контура остается слева по отношению к движущейся по контуру точке, то такое направление обхода кривой назовем положительным, а противоположное ему – отрицательным.

Криволинейный интеграл вдоль замкнутой кривой не зависит от выбора начальной точки пути, а зависит лишь от направления обхода

Интеграл по замкнутому контуру обозначается и

называется циркуляцией вектора по замкнутому контуру .

4. Вычисление криволинейного интеграла 2-го рода.

Вычисляют криволинейный интеграл сведением его к определенному интегралу. Для преобразования криволинейного интеграла в определенный, следует всюду под знаком криволинейного интеграла заменить переменные их выражениями через параметр и после этого рассматривать интеграл как определенный по параметру, взятый в пределах изменения параметра.

1. Пусть - плоская гладкая кривая, заданная уравнением , .

Тогда справедливо равенство

2. Пусть плоская кривая задана параметрически

, , функции непрерывны и имеют непрерывные производные . Тогда

.

3. Если пространственная кривая задана параметрически:

где функции - непрерывны и имеют непрерывные производные, то

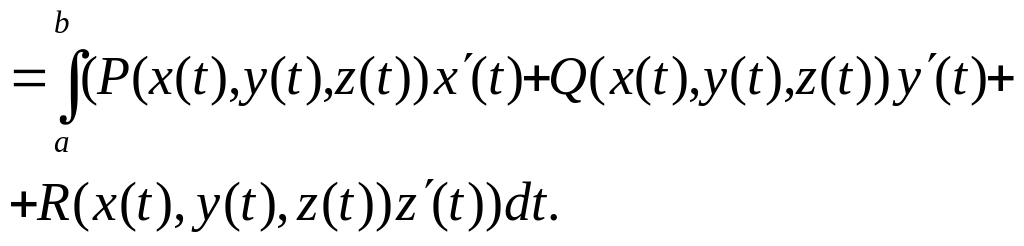
4. Если кривая задана уравнениями , ,

то принимая за параметр, получим:

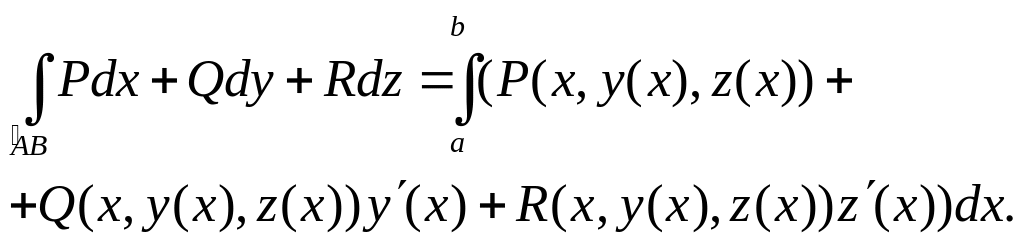
Примеры. 1. Вычислить криволинейный интеграл второго

рода

вдоль отрезка прямой от точки до ).

Решение. Составим параметрические уравнения прямой, проходящей через точки и :

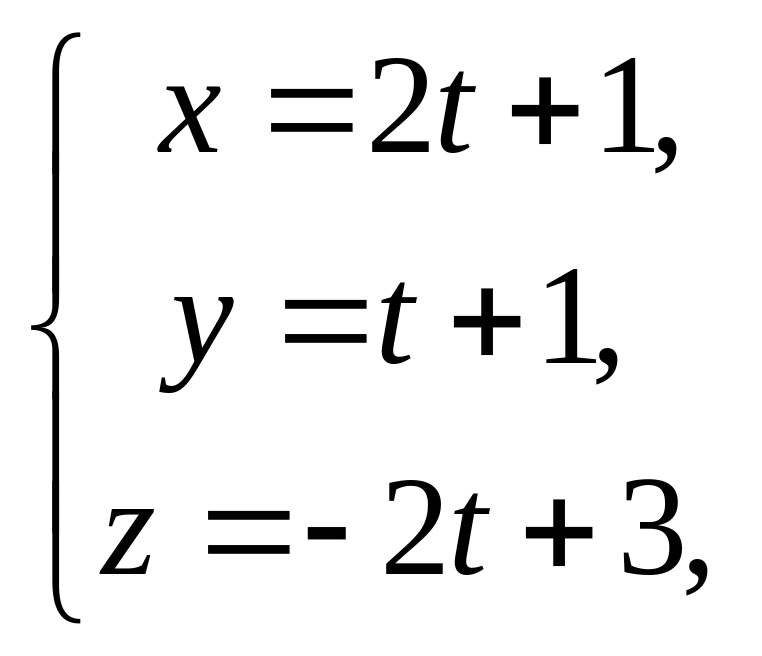тогда

Точке соответствует точке соответствует

Следовательно,

2.Вычислить вдоль дуги параболы

от точки до

Решение. Принимая за параметр, перейдем к определенному интегралу

3. Вычислить криволинейный интеграл второго рода , где - окружность

Решение. Запишем параметрические уравнения данной

окружности : Найдем . Получим

4. Вычислить криволинейный интеграл второго рода

где кривая , пробегаемая в направлении возрастания параметра .

Решение. Найдем , тогда

5. Вычислить криволинейный интеграл

,

вдоль замкнутого контура , являющегося границей части сферы , расположенной в I октанте: причем направление обхода контура таково, что в плоскости движение происходит от точки к точке

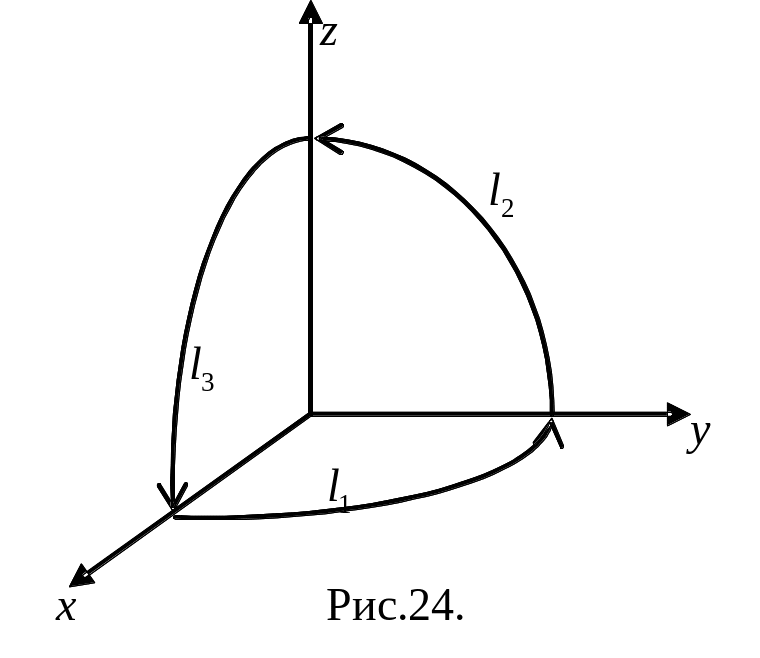Решение. Контур состоит из трех кривых , каждая из которых является дугой единичной окружности, лежащей соответственно в координатных плоскостях (рис.24). Поэтому , где

Найдем интеграл по кривой . Так как кривая лежит в

плоскости , то и где Запишем параметрические уравнения Получим

Точно также вычисляются интегралы . При этом Следовательно,

Задачи и упражнения для самостоятельной работы

Вычислить криволинейные интегралы второго рода:

1. где , если a) ОА- отрезок

прямой; б) ОА- дуга параболы, осью которой является ось ; в) ОА- ломаная линия состоящая из отрезка ОВ оси и отрезка ВА, параллельного оси .

2. где - дуга параболы:

3. где - кривая

4. где - эллипс

5. где - арка циклоиды

6. где - окружность

7. где - граница квадрата с вершинами А(1,0), В(0,1), С(-1,0), D(0,-1).

8. где - виток винтовой линии

9. где - кривая Вивиани , пробегаемая против часовой стрелки, если смотреть из точки .

10. Вычислить работу силы вдоль кривой АВ, если:

а) АВ – окружность , пробегаемая по

ходу часовой стрелки от точки А(-1/ до точки ;

б) АВ – виток винтовой линии