
- •Колебания и волны
- •Введение
- •Механические колебания Основные формулы
- •Примеры решения задач
- •Волны в упругой среде. Акустика Основные формулы
- •Примеры решения задач
- •Электрические колебания. Переменный ток. Электромагнитные волны Основные формулы
- •Примеры решения задач
- •Основные физические постоянные
- •Десятичные приставки к названиям единиц (10n)
- •Плотность вещества ρ, 103 кг/м3
- •Упругость
- •Вязкость η, 10-3 Па∙с
- •Оглавление
- •Колебания и волны
Примеры решения задач
Пример
1. Амплитуда
гармонического колебания
 ,
период
,
период
 .
Найти максимальную скорость
.
Найти максимальную скорость
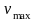 колеблющейся точки и ее максимальное
ускорение
колеблющейся точки и ее максимальное
ускорение
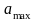 .
.
Решение.
Уравнение гармонического колебательного
движения точки имеет вид:
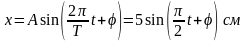 .
Начальная фаза
неизвестна
и далее будет показано, что она не
требуется для решения задачи. Скорость
v
колеблющейся точки по определению равна
.
Начальная фаза
неизвестна
и далее будет показано, что она не
требуется для решения задачи. Скорость
v
колеблющейся точки по определению равна
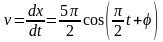 .
Таким образом, скорость точки изменяется
по гармоническому закону с амплитудой
(максимальным значением)
.
Таким образом, скорость точки изменяется
по гармоническому закону с амплитудой
(максимальным значением)
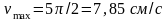 .
Ускорение a
колеблющейся точки по определению равно
.
Ускорение a
колеблющейся точки по определению равно
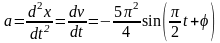 .
Следовательно, ускорение точки также
изменяется по гармоническому закону с
амплитудой (максимальным значением)
.
Следовательно, ускорение точки также
изменяется по гармоническому закону с
амплитудой (максимальным значением)
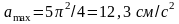 .
.
Пример
2. Найти
амплитуду A
и начальную фазу
гармонического колебания, полученного
от сложения одинаково направленных
колебаний, данных уравнениями
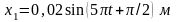 и
и
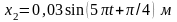 .
.
Решение.
Амплитуда суммы одинаково направленных
гармонических колебаний одинаковой
частоты (периода) рассчитывается по
формуле
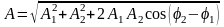 .
По условию задачи:
.
По условию задачи:
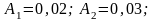
 .
Следовательно,
.
Следовательно,
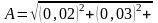
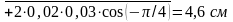 .
Начальная фаза суммарного колебания
определяется из уравнения
.
Начальная фаза суммарного колебания
определяется из уравнения

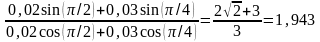 .
Следовательно,
.
Следовательно,
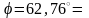
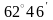 .
.
Пример
3. Бревно
массы
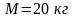 висит на двух шнурах длины
висит на двух шнурах длины
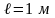 каждый. В торец бревна попадает и
застревает в нем пуля массы
каждый. В торец бревна попадает и
застревает в нем пуля массы
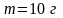 ,
летящая со скоростью
,
летящая со скоростью
 .
Найти амплитуду
.
Найти амплитуду
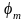 и период T
колебаний бревна. Трением пренебречь.
и период T
колебаний бревна. Трением пренебречь.
Решение.
Бревно на шнурах длиной
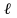 можно считать математическим маятником,
период колебаний T
которого
рассчитывается по формуле:
можно считать математическим маятником,
период колебаний T
которого
рассчитывается по формуле:
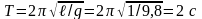 ,
где
,
где
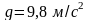 – ускорение свободного падения. Попадание
и застревание пули в бревне является
абсолютно неупругим ударом, для которого
закон сохранения импульса записывается
как:
– ускорение свободного падения. Попадание
и застревание пули в бревне является
абсолютно неупругим ударом, для которого
закон сохранения импульса записывается
как:
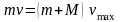 .
Следовательно, максимальная скорость
бревна с пулей
.
Следовательно, максимальная скорость
бревна с пулей
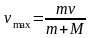 .
Бревно с пулей будет совершать
гармонические колебания
.
Бревно с пулей будет совершать
гармонические колебания
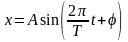 .
Скорость бревна, в свою очередь,
.
Скорость бревна, в свою очередь,
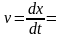
 .
Максимальная скорость бревна (амплитуда
скорости)
.
Максимальная скорость бревна (амплитуда
скорости)
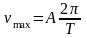 .
Следовательно,
.
Следовательно,
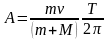 .
Угловая амплитуда
малых колебаний бревна связана с
амплитудой A
линейных колебаний соотношением:
.
Угловая амплитуда
малых колебаний бревна связана с
амплитудой A
линейных колебаний соотношением:
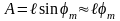 .
Приближенное равенство выполняется
для малых углов:
.
Приближенное равенство выполняется
для малых углов:
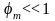 .
Окончательно для угловой амплитуды
колебаний бревна получаем
.
Окончательно для угловой амплитуды
колебаний бревна получаем
 .
.
Пример
4. Период
затухающих колебаний
;
логарифмический декремент затухания
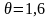 ;
начальная фаза
;
начальная фаза
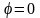 .
При
.
При
 смещение точки
смещение точки
 .
Написать уравнение движения этого
колебания.
.
Написать уравнение движения этого
колебания.
Решение.
Уравнение затухающего колебательного
движения имеет вид
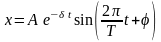 .
Коэффициент затухания
.
Коэффициент затухания
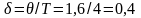 .
Следовательно,
.
Следовательно,
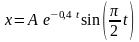 .
Амплитуду A
затухающих колебаний находим из условия
.
Амплитуду A
затухающих колебаний находим из условия
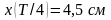 .
Следовательно,
.
Следовательно,
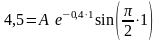 .
Получаем, что
.
Получаем, что
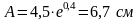 .
Окончательно уравнение затухающих
колебаний:
.
Окончательно уравнение затухающих
колебаний:
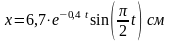 .
.
Пример
5. Тело массой
совершает затухающие колебания с
максимальной амплитудой
 ,
начальной фазой
и коэффициентом затухания
,
начальной фазой
и коэффициентом затухания
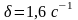 .
На это тело начала действовать внешняя
периодическая сила F,
под действием которой установились
вынужденные колебания. Уравнение
вынужденных колебаний имеет вид
.
На это тело начала действовать внешняя
периодическая сила F,
под действием которой установились
вынужденные колебания. Уравнение
вынужденных колебаний имеет вид
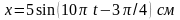 .
Найти (с числовыми коэффициентами)
уравнение собственных колебаний и
уравнение внешней периодической силы.
.
Найти (с числовыми коэффициентами)
уравнение собственных колебаний и
уравнение внешней периодической силы.
Решение.
Уравнение собственных затухающих
колебаний имеет вид
 .
Сдвиг фаз между собственными и вынужденными
колебаниями равен
.
Сдвиг фаз между собственными и вынужденными
колебаниями равен
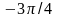 .
Следовательно,
.
Следовательно,
 и
и
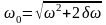 ,
где частота вынужденных колебаний
,
где частота вынужденных колебаний
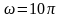 и коэффициент затухания
.
Следовательно,
и коэффициент затухания
.
Следовательно,
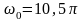 .
Тогда уравнение собственных колебаний:
.
Тогда уравнение собственных колебаний:
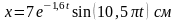 .
Уравнение внешней периодической силы:
.
Уравнение внешней периодической силы:
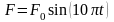 ,
где
,
где
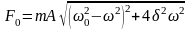 (
– амплитуда вынужденных колебаний).
Получаем
(
– амплитуда вынужденных колебаний).
Получаем
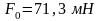 .
Следовательно, уравнение внешней
периодической силы:
.
Следовательно, уравнение внешней
периодической силы:
 .
.
Задачи
1.1.
Точка совершает колебания с амплитудой
А=4см
и периодом Т=2с.
Написать уравнение этих колебаний,
считая, что в момент t=0 смещения x(0)=0
и
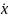 (0)<0.
Определить фазу (ωt+φ) для двух моментов
времени: 1) когда смещение x=1 см и
>0;
2) когда скорость
=-6
см/с и х<0. (x= А cos
(ωt+φ), где А= 4 см, ω=2π/Т=π рад/с, φ=π/2 рад;
1)5π/3 рад; 2)0,842π рад).
(0)<0.
Определить фазу (ωt+φ) для двух моментов
времени: 1) когда смещение x=1 см и
>0;
2) когда скорость
=-6
см/с и х<0. (x= А cos
(ωt+φ), где А= 4 см, ω=2π/Т=π рад/с, φ=π/2 рад;
1)5π/3 рад; 2)0,842π рад).
1.2.
Определить максимальные значения
скорости
max
и
ускорения
 max
точки, совершающей гармонические
колебания с амплитудой А=3
см и угловой частотой ω=π/2 с-1.
(4,71 см/с; 7,40 см/с2).
max
точки, совершающей гармонические
колебания с амплитудой А=3
см и угловой частотой ω=π/2 с-1.
(4,71 см/с; 7,40 см/с2).
1.3.
Точка совершает колебания по закону
x=Аcosωt, где А
=5 см; ω = 2с-1.
Определить ускорение |
|
точки в момент времени, когда ее скорость
=
8 см/с. (|
|=
ω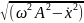 =12
см/с2).
=12
см/с2).
1.4. Точка совершает гармонические колебания. Наибольшее смещение xmax точки равно 10 см, наибольшая скорость max = 20 см/с. Найти угловую частоту ω колебаний и максимальное ускорение max точки. (2 с-1; 40 см/с2).
1.5.
Максимальная скорость
max
точки, совершающей гармонические
колебания, равна 10см/с, максимальное
ускорение
max=100
см/с2.
Найти угловую частоту ω колебаний, их
период Т
и амплитуду А.
Написать уравнение колебаний, приняв
начальную фазу равной нулю. (10 с-1;
0,628 с; 1 см;
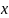 =
А cos
ωt).
=
А cos
ωt).
1.6.
Точка совершает колебания по закону
х=Аsinωt .В некоторый момент времени
смещение x1
точки оказалось равным 5 см. Когда фаза
колебаний увеличилась вдвое, смещение
x2
стало равным 8 см. Найти амплитуду А
колебаний. (А=2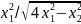 =8,33 см).
=8,33 см).
1.7.
Колебания точки происходят по закону
х=Acos(ωt/+φ).В некоторый момент времени
смещение x точки равно 5 см, ее скорость
=20
см/с и ускорение
=-80
см/с2.
Найти амплитуду А,
угловую частоту ω, период Т
колебаний и фазу (ωt/+φ) в рассматриваемый
момент времени. (ω=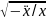 =4
с-1;
Т=2π/ω=1,57 с; А=
=4
с-1;
Т=2π/ω=1,57 с; А=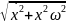 =7,07
см; ωt+φ=arcos(x/А)=
π/4 рад).
=7,07
см; ωt+φ=arcos(x/А)=
π/4 рад).
Сложение колебаний
1.8. Два одинаково направленных гармонических колебания одного периода с амплитудами А1=10 см и А2=6 см складываются в одно колебание с амплитудой А=14 см. Найти разность фаз ∆φ складываемых колебаний. (π/3 рад).
1.9. Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз ∆φ складываемых колебаний. (2π/3 рад или 4π/3 рад).
1.10. Определить амплитуду А и начальную фазу φ результирующего колебания, возникающего при сложении двух колебаний одинаковых направления и периода: x1=А1 sin ωt и x2=А2 sin ω(t+τ), где А1=А2=1 см; ω=π с-1; τ=0,5 с. Найти уравнение результирующего колебания. (А=1,41 см; φ=π/4 рад; x = А cos (ωt+φ), где ω = π с-1).
1.11. Точка участвует в двух одинаково направленных колебаниях: x1=А1sinωt и x2=А2cos ωt, где А1=1 см; А2=2 см; ω=1 с-1. Определить амплитуду А результирующего колебания, его частоту ν и начальную фазу φ. Найти уравнение этого движения. (А=2,24 см; ν=0,159 Гц; φ=0,353π рад; x= А cos (ωt+φ), где ω=1 с-1).
1.12. Складываются два гармонических колебания одного направления с одинаковыми периодами Т1=Т2=1,5 с и амплитудами А1=А2=2 см. Начальные фазы колебаний φ1=π/2 и φ2=π/3. Определить амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд. (А=3,86 см; φ=0,417π рад; x= А cos (ωt+φ), где ω=2π/Т с-1 = 4,19 с-1).
1.13. Складываются три гармонических колебания одного направления с одинаковыми периодами Т1=Т2=Т3=2 с и амплитудами А1=А2=А3=3 см. Начальные фазы колебаний φ1=0, φ2=π/3, φ3=2π/3. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение. (А= 6 см; φ= π/3 рад; x= А cos (ωt+φ), где ω=2π/Т с-1=π с-1).
1.14. Складываются два гармонических колебания одинаковой частоты и одинакового направления: x1= А1cos(ωt+φ1) и x2=А2cos(ωt+φ2). Начертить векторную диаграмму для момента времени t=0. Определить аналитически амплитуду А и начальную фазу φ результирующего колебания. Отложить А и φ на векторной диаграмме. Найти уравнение результирующего колебания (в тригонометрической форме через косинус). Задачу решить для двух случаев: 1) А1=1 см, φ1=π/3; А2=2 см, φ2=5π/6; 2) А1=1 см, φ1=2π/3; А2=1 см, φ2=7π/6. (1) А= 2,24см; φ= 0,686π рад; 2) А= 1,41см; φ=0,917π рад).
1.15. Два камертона звучат одновременно. Частоты ν1 и ν2 их колебаний соответственно равны 440 и 440,5 Гц. Определить период Т биений. (2с).
1.16. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями х=А1sin ωt и y=А2cosω(t+τ), где А1 = 2 см, А2=1 см, ω= π с-1, τ=0,5 с. Найти уравнение траектории и построить ее, показав направление движения точки. (y= - (А2/А1)x или y= - 1/2x).
1.17. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями х=А1cosωt и y=А2cosω(t+τ), где А1=4 см, А2=8 см, ω=π с-1, τ =1 с. Найти уравнение траектории точки и построить график ее движения. (y= - (А2/А1)x или y= - 2x).
1.18.
Точка
совершает одновременно два гармонических
колебания одинаковой частоты, происходящих
по взаимно перпендикулярным направлениям
и
выражаемых
уравнениями: 1)
х=Аcosωt
и y=Аcosωt;
2)
х=Асosωt
и y=А1cosωt;
3)
х=Аcosωt
и y=Аcos(ωt+φ1);
4)
х=А2cosωt
и y=Аcos(ωt+φ2);
5)
х=А1cosωt
и y=А1sinωt;
6)
х=Аcosωt
и y=А1sinωt;
7)
х=А2sinωt
и y=А1sinωt;
8)
х=А2sinωt
и y=Аsin(ωt+φ2).
Найти для восьми случаев: уравнение
траектории точки, построить ее с
соблюдением масштаба и указать направление
движения. Принять: А=2
см, А1=3
см, А2=
1 см; φ1=π/2,
φ2=π.
(1) y=
x; 2) y
= (А2/А1)x,
y
=
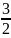 x;
3) x2+y2=А2,
x2+y2=4;
4) y=
- (А2/А1)x,
y=
- 2x; 5) x2+y2=А2,
x2+y2=9;
6)
x;
3) x2+y2=А2,
x2+y2=4;
4) y=
- (А2/А1)x,
y=
- 2x; 5) x2+y2=А2,
x2+y2=9;
6)
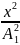 +
+ =1,
=1,
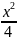 +
+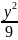 =1;
7) y= (А2/А1)x,
y=3x; 8) y=-(А2/А1)x,
y=-2x).
=1;
7) y= (А2/А1)x,
y=3x; 8) y=-(А2/А1)x,
y=-2x).
1.19.
Точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями х=А1cosωt
и y=А2
sinωt,
где А1=2
см, А2=1
см. Найти уравнение траектории точки и
построить ее, указав направление
движения. (
+
=1,
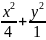 =1).
=1).
1.20.
Точка
одновременно совершает два гармонических
колебания, происходящих по взаимно
перпендикулярным направлениям и
выражаемых уравнениями
х=А1sinωt
и y=А2cosωt,
где А1=0,5
см; А2=2
см. Найти уравнение траектории точки и
построить ее, указав направление
движения. ( = 1).
= 1).
1.21.
Движение точки задано уравнениями
х=А1sinωt
и y=А2sinω(t+τ),
где А1=10
см,
А2=5
см, ω=2
с-1,
τ=π/4 с. Найти уравнение траектории и
скорость точки в момент времени t =0,5с.
(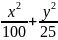 =1,
υ = 13,7
м/с).
=1,
υ = 13,7
м/с).
1.22.
Материальная
точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями
х=А1cosωt
и y=-А2cos2ωt,
где А1=2
см,
А2=1
см. Найти уравнение траектории и построить
ее. (y=-2(А2/А1)x2+А2,
y=-(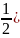 x2+1).
x2+1).
1.23.
Точка участвует одновременно в двух
гармонических колебаниях, происходящих
по взаимно перпендикулярным направлениям
и описываемых уравнениями: 1)
х=Аsinωt
и y=Аcos2ωt;
2)
х=Аcosωt
и y=Аsin2ωt;
3)
х=Аcos2ωt
и y=А1cosωt;
4)
х=А1sinωt
и y=Аcosωt.
Найти уравнение траектории точки,
построить ее с соблюдением масштаба и
указать направление движения. Принять:
А=2 см; А1=3
см. (1)
y=А-2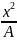 ,y=-x2+2;
2) y=2
-А,
y=x2-2;
3) 2Аy-А1x2=АА1,
y=¾x2+
;
4) x=2(А1/А)y
,y=-x2+2;
2) y=2
-А,
y=x2-2;
3) 2Аy-А1x2=АА1,
y=¾x2+
;
4) x=2(А1/А)y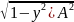 ,
x=
y
,
x=
y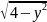 ).
).
1.24.
Точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями
х=А1cosωt
и y=А2sin0,5ωt,
где А1=
2 см, А2=3
см. Найти уравнение траектории точки
и построить ее, указав направление
движения. (y= (А1-x),
x=
(А1-x),
x=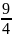 (2-x)).
(2-x)).
1.25. Смещение светящейся точки на экране осциллографа является результатом сложения двух взаимно перпендикулярных колебаний, которые описываются уравнениями: 1) х=Аsin3ωt и y=А sin2ωt; 2) х=Аsin3ωt и y=Аcos2ωt; 3) х=Аsin3ωt и y=Аcosωt. Применяя графический метод сложения и соблюдая масштаб, построить траекторию светящейся точки на экране. Принять А =4см. (Самостоятельно).
Динамика гармонических колебаний. Маятники
1.26. Грузик массой m=250 г, подвешенный к пружине, колеблется по вертикали с периодом Т=1 с. Определить жесткость k пружины. (9,87 Н/м).
1.27. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на х=9 см. Каков будет период Т колебаний грузика, если его немного оттянуть вниз и затем отпустить? (0,6 с).
1.28. Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой А=4 см. Определить полную энергию Е колебаний если жесткость k пружины равна 1 кН/м. (0,8 Дж).
1.29.
Найти
отношение длин двух математических
маятников, если отношение периодов их
колебаний равно 1,5. (
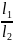 =
-(
=
-(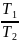 )2=2,25
.
)2=2,25
.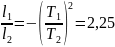 ).
).
1.30.
Математический маятник длиной 𝓁=1
м установлен в лифте. Лифт поднимается
с ускорением а=2,5
м/с2.
Определить период Т
колебаний маятника. (Т=2π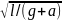 =1,8
с).
=1,8
с).
1.31.
Тонкий
обруч, повешенный на гвоздь, вбитый
горизонтально в стену, колеблется в
плоскости, параллельной стене. Радиус
R
обруча
равен 30 см. Вычислить период Т
колебаний
обруча. (Т=2π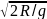 =1.55
c).
=1.55
c).
1.32.
Однородный
диск радиусом R=30
см
колеблется около горизонтальной
оси, проходящей через одну из образующих
цилиндрической поверхности диска. Каков
период Т
его
колебаний? (Т=2π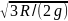 =1.35
c).
=1.35
c).
1.33. Диск радиусом R=24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину L и период Т колебаний такого маятника. (36 см).
1.34. Математический маятник длиной 𝓁1=40 см и физический маятник в виде тонкого прямого стержня длиной 𝓁2=60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние, a центра масс стержня от оси колебаний. (10 см).
1.35. Верхний конец стальной проволоки диаметром 0,5 мм и длинной 80 см защемлён. К нижнему концу проволоки прикреплён шар массой 2 кг и диаметром 10 см. Если шар повернуть вокруг вертикальной оси на небольшой угол и отпустить, он будет совершать вращательные колебания. Определите период колебаний шара. (11,5 с).
1.36. Тонкая прямоугольная пластинка может колебаться вокруг горизонтальной оси, лежащей в ее плоскости и перпендикулярной одной из ее сторон, длина которой равна 𝓁.
а) Каков период колебаний, если ось совпадает с верхней стороной пластинки?
б)
При каком расстоянии оси от середины
пластинки период колебаний пластинки
будет наименьшим? Каков этот период?
(1) 2π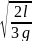 ;
2)
;
2)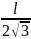 ;
2π
;
2π ).
).
1.37. Шар радиусом 5 см подвешен на нити длиной 10 см. Определите погрешность, которую мы делаем, приняв его за математический маятник длиной 15 см. (2,2%).
Затухающие колебания
1.38. Амплитуда затухающих колебаний маятника за время t1=5 мин уменьшилась в два раза. За какое время t2, считая от начального момента, амплитуда уменьшится в восемь раз? (15 мин).
1.39. За время t=8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания δ. (0,0023 с-1).
1.40.
Амплитуда колебаний маятника длиной
l=1 м за время t=10 мин уменьшилась в два
раза. Определить логарифмический
декремент колебаний Ө. (Ө =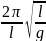 ln
ln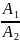 = 2,31·10-3).
= 2,31·10-3).
1.41.
Логарифмический декремент колебаний
Ө маятника равен 0,003. Определить число
N
полных
колебаний, которые должен сделать
маятник, чтобы амплитуда уменьшилась
в два раза. (N=
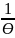 ln
=231).
ln
=231).
1.42.
Гиря массой m=500
г подвешена к спиральной пружине
жесткостью k
=20
Н/м и совершает упругие колебания в
некоторой среде. Логарифмический
декремент колебаний Ө=0,004. Определить
число N
полных
колебаний, которые должна совершить
гиря, чтобы амплитуда колебаний
уменьшилась в п=2
раза.
За какое время t
произойдет это уменьшение? (N=
ln
=173;
t=2πn = 2 мин 52 с).
= 2 мин 52 с).
1.43. Тело массой m=5 г совершает затухающие колебания. В течение времени t =50 с тело потеряло 60% своей энергии. Определить коэффициент сопротивления b. (9,16·10-5 кг/с).
1.44.Определить период Т затухающих колебаний, если период Т0 собственных колебаний системы равен 1с и логарифмический декремент колебаний Ө =0,628. (1,005).

Рис.1
1.46. Тело массой m=1 кг находится в вязкой среде с коэффициентом сопротивления b=0,05 кг/с. С помощью двух одинаковых пружин жесткостью k=50 Н/м каждое тело удерживается в положении равновесия, пружины при этом не деформированы (рис. 1). Тело сместили от положения равновесия и отпустили. Определить: 1) коэффициент затухания δ; 2) частоту ν колебаний; 3) логарифмический декремент колебаний Ө; 4) число N колебаний, по прошествии которых амплитуда уменьшится в е раз. (1) 0,025; 2) 1,59Гц; 3) 0,0157; 4) 64).
1.47. Начальная амплитуда колебаний маятника равна 3 см. Через 10 с она стала равной 1 см. Через сколько времени амплитуда колебаний будет равна 0,3 см? (21 с).
1.48. Каков логарифмический декремент затухания маятника длиной 0,8 м, если его начальная амплитуда равна 5°, а через 5 мин она становится равной 0,5°? (0,014).
1.49.
Через сколько времени энергия колебаний
камертона с частотой f
=600
Гц уменьшится в n=106
раз, если логарифмический декремент
затухания равен 0,0008?
(t =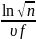 =14 с).
=14 с).
1.50. Какова общая сумма путей, пройденных колеблющейся точкой до полного затухания колебаний, если амплитуда первого колебания равна 1 мм, а логарифмический декремент затухания равен 0,002? (2 м).
Вынужденные колебания. Резонанс
1.51.
Под действием силы тяжести электродвигателя
консольная балка, на которой он установлен,
прогнулась на
h=1 мм.
При какой частоте вращения n
якоря
электродвигателя может возникнуть
опасность резонанса? (n=
 =16 с-1).
=16 с-1).
1.52.
Вагон массой m=80
т имеет четыре рессоры. Жесткость k
пружин
каждой рессоры равна 500 кН/м. При какой
скорости υ
вагон
начнет сильно раскачиваться вследствие
толчков на стыках рельс, если длина 𝓁
рельса
равна 12,8 м? (υ=(l/π)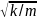 =10,2
м/с).
=10,2
м/с).
1.53. Колебательная система совершает затухающие колебания с частотой ν=1000 Гц. Определить частоту ν0 собственных колебаний, если резонансная частота vpeз=998 Гц. (1002 Гц).
1.54. Определить, на сколько резонансная частота отличается от частоты ν0=l кГц собственных колебаний системы, характеризуемой коэффициентом затухания δ=400 с-1. (Δν= δ2/(4π2 ν0)=4,05 Гц).
1.55.
Определить логарифмический декремент
колебаний Ө колебательной системы, для
которой резонанс наблюдается при
частоте, меньшей собственной частоты
ν0=10
кГц на ∆ν=2 Гц. (θ=2π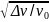 =0,089).
=0,089).
1.56.
Период Т0
собственных
колебаний пружинного маятника равен
0,55 с. В вязкой среде период Т
того
же маятника стал равным 0,56 с. Определить
резонансную частоту νpeз
колебаний. (νpeз=
 =1,75
с-1).
=1,75
с-1).
1.57. Пружинный маятник (жесткость k пружины равна 10 Н/м, масса m груза равна 100 г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r=2·10-2 кг/с. Определить коэффициент затухания δ и резонансную амплитуду Арез, если амплитудное значение вынуждающей силы F0=10 мН. (0,1 с-1; 5 см).
1.58. Тело совершает вынужденные колебания в среде с коэффициентом сопротивления r=1 г/с. Считая затухание малым, определить амплитудное значение вынуждающей силы, если резонансная амплитуда Арез=0,5 см и частота ν0 собственных колебаний равна 10 Гц с-1. (F0=2πν0rАрез=0,314 мН).
1.59. Амплитуды вынужденных гармонических колебаний при частоте ν1=400 Гц и ν2=600 Гц равны между собой. Определить резонансную частоту vpeз. Затуханием пренебречь. (510 Гц).
1.60.К спиральной пружине жесткостью k=10 Н/м подвесили грузик массой m=10 г и погрузили всю систему в вязкую среду. Приняв коэффициент сопротивления b равным 0,1 кг/с, определить: 1) частоту ν0 собственных колебаний; 2) резонансную частоту νpcз; 3) резонансную амплитуду Арез, если вынуждающая сила изменяется по гармоническому закону и ее амплитудное значение F0=0,02 Н; 4) отношение резонансной амплитуды к статическому смещению под действием силы F0. (1) 5,03 Гц; 2) 4,91 Гц; 3) 6,4 мм; 4) 3,2).
1.61. Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты: 1)на 10%? 2)в два раза? Коэффициент затухания δ в обоих случаях принять равным 0,1 ω0 (ω0 − угловая частота собственных колебаний). (1) 1,53; 2) 15,2).
1.62.
Амплитуда смещения вынужденных колебаний
при очень малой частоте равна s0=2
мм, а при резонансе равна s=16 мм, Предполагая,
что декремент затухания меньше единицы,
определите его. (s
=
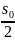 (
(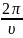 +
+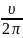 );
при υ<1 можно принять, что s =
);
при υ<1 можно принять, что s =
 ,
откуда υ=
=0,4).
,
откуда υ=
=0,4).
