2.2 Общие уравнения чувствительности

Введем в рассмотрение вектор параметров , то можно написать векторное уравнение

. (2.20)

Далее, не оговаривая это особо, будем предполагать, что при любом , где - область возможного изменения вектора , для системы (2.20) выполнены условия существования, единственности и продолжимости решений при .

Одной из основных задач теории чувствительности является изучение свойств решений уравнения (2.20) в функции от .

Может так же быть рассмотрен вопрос о зависимости решений уравнений (2.20) от начальных данных, которые так же входят в качестве параметров в общую параметрическую модель конечномерной системы.

Если выполнены условия теоремы о дифференцируемости по параметрам, то, имея исходную систему (2.20), можно получить систему дифференциальных уравнений, определяющих производную решений по параметрам. Этот факт определяется следующим утверждением.

Пусть выполнены условия интегральной теоремы о дифференцируемости решений по параметрам, причем и от A не зависят. Тогда производные от решений по параметрам определяются дифференциальными уравнениями[70]

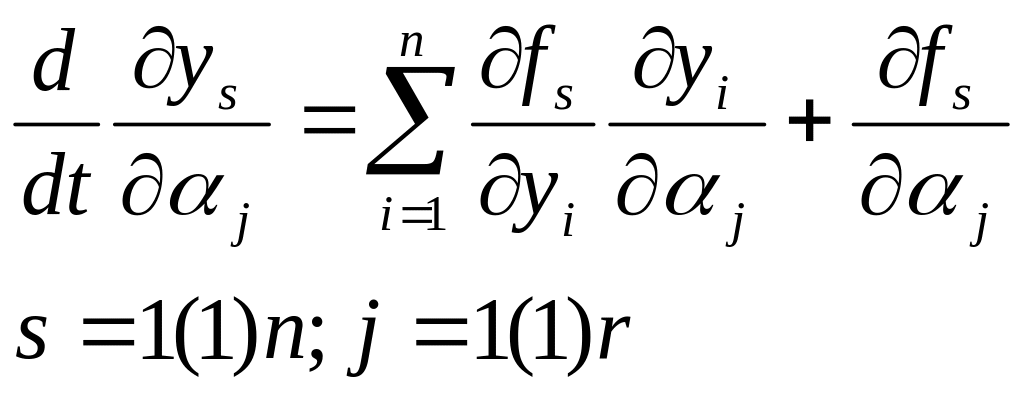(2.21)

с начальными условиями

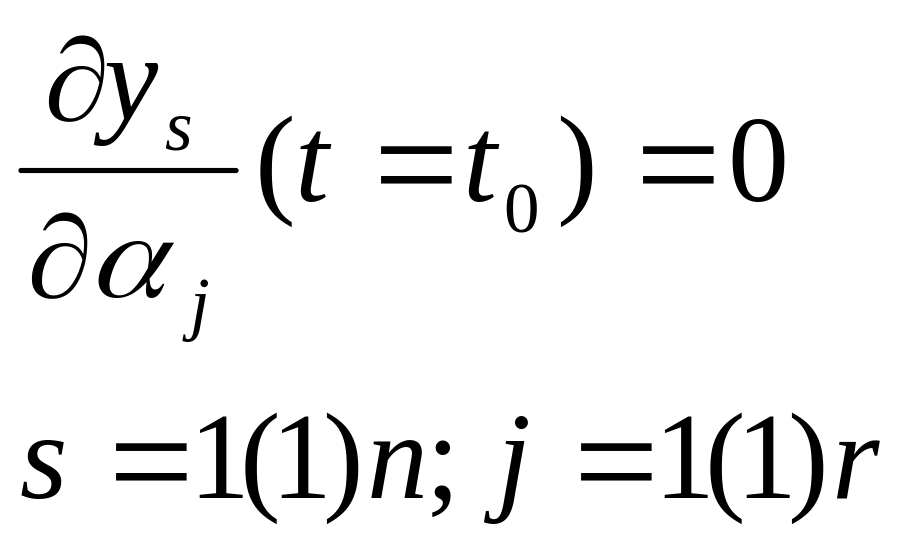(2.22)

Легко заметить, что уравнения (2.22) получаются из (2.20) формальным дифференцированием по . Таким образом, мы пришли к уравнениям чувствительности системы по параметру [55, 19].

Из приведенной теоремы непосредственно могут быть получены уравнения для определения производных по начальным условиям . Эти производные удовлетворяют уравнениям вида

, (2.23)

которые получаются из (2.22) отбрасыванием второго слагаемого из правой части. Уравнения (2.23) называются уравнениями в вариациях [113].

Рассмотрим уравнение (2.20) для того случая, когда вместо вектора параметров A имеется один скалярный параметр

. (2.24)

Этот параметр определяет полную группу и однопараметрическое семейство решений, если начальные условия однозначно зависят от .

, . (2.25)

Если функции [135, 113] (2.25) непрерывно дифференцируемы по , то решение , удовлетворяющее условиям

, (2.26)

непрерывно дифференцируемо по на любом замкнутом интервале t, при котором решение принадлежит области , в которой правая часть уравнения (2.24) непрерывно дифференцируема по Y, . При этом производная (описывающая функцию чувствительности по параметру )

(2.27)

определяется уравнением

(2.28)

и начальными условиями

(2.29)

В (2.28) производная от вектора F по вектору Y является квадратной матрицей

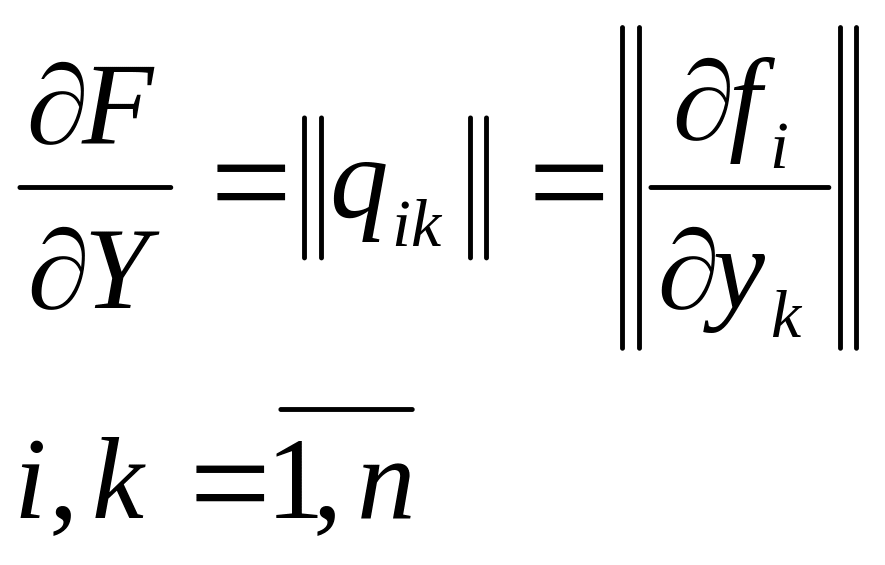. ( 2.30)

Из вышесказанного следует:

Из (2.27) можно сделать вывод, что вид уравнений, определяющих функцию , не зависит от начальных условий (2.25), т.е. не зависит от выбора конкретного семейства решений, и определяется исключительно зависимостью правой части (2.24) от . Поэтому уравнение (2.28) будем называть векторным уравнением чувствительности информационной системы по параметру . Функции чувствительности по различных однопараметрических семейств решений удовлетворяют одному и тому же уравнению (2.28), но с различными начальными условиями (2.29) [26].

Как следует из уравнения (2.28), уравнения чувствительности по параметру линейны относительно соответствующих функций чувствительности. В общем случае эти уравнения неоднородны и являются однородными лишь тогда, когда

, (2.31)

т.е. когда правая часть уравнения (2.28) фактически не зависит от параметра на рассматриваемом семействе решений [71,72,73].

– Если исходная система зависит еще от двух скалярных параметров и , то вместо (2.24) имеем

. (2.32)

При выполнении соответствующих условий дифференцируемости можно написать уравнение чувствительности по параметру :

, (2.33)

где - функция чувствительности по параметру .

Сравнение (2.29) и (2.33) показывает, что эти уравнения отличаются лишь свободными членами. Их одинаковая однородная часть описывается уравнением

, (2.34)

которое совпадает с уравнением в вариациях (132).