
- •Волновые процессы
- •1. Волны, их основные типы и характеристики. (табл. 4.41, табл. 4.42)
- •Продольные и поперечные волны (табл. 4.43)
- •Гармоническая волна и ее описание (табл. 4.45).
- •Плоские и сферические волны (табл. 4.44).
- •Уравнение волны (табл. 4.47) (Савельев)
- •5. Энергия волны
- •6. Принцип суперпозиции волн (табл. 4.2.3)
- •7. Интерференция волн (табл. 4.2.4).
- •8.Стоячие волны (табл. 4.2.5). .
Гармоническая волна и ее описание (табл. 4.45).
Плоские и сферические волны (табл. 4.44).
Однородная среда - среда, физические свойства которой не изменяются от точки к точке среды.
Изотропная среда -
Геометрическое место точек, до которых доходят колебания к моменту времени t,называетсяфронтом волны.Это поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называетсяволновой поверхностью.
Если волновые поверхности – параллельные плоскости, то волна называется плоской;
если волновые поверхности – концентрические сферы с центром в источнике волны, волна называется сферической.
ЛУЧ -
Уравнение волны (табл. 4.47) (Савельев)
Уравнением
волны называется
зависимость от координат и времени
параметров среды при прохождение в ней
волны
![]() (имеются в виду координаты равновесного
положения частицы). Эта
функция должна быть периодической как
относительно времени, так и относительно
координат.
(имеются в виду координаты равновесного
положения частицы). Эта
функция должна быть периодической как
относительно времени, так и относительно
координат.
Периодичность
по времени вытекает
из того, что
ξ описывает
колебания частицы с координатами
![]() .
.
Периодичность по координатам вытекает из того, что точки, отстоящие друг от друга на расстоянии λ, колеблются одинаковым образом.
1.
Найдем функцию
![]() в случаеплоской поперечной
волны, полагая,
что
в случаеплоской поперечной
волны, полагая,
что
к
 олебания
носят гармонический характер, а волна
распространяется в направлении осиХ
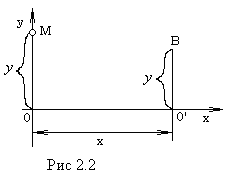
(рис.2.2).
олебания
носят гармонический характер, а волна
распространяется в направлении осиХ
(рис.2.2). Рассмотрим точку М, которая являетсяисточником колебаний.
- Ее колебания
относительно положения равновесия
(точки О) описываются уравнением![]()
- время tбудем отсчитывать от начала колебаний точкиМ.
- Через время колебания достигают точкиВ, которая начинает колебаться относительно своего положения равновесия точкиО /.
- Волновой процесс распространяется при этом на расстояние ОО/=x.
Найдем уравнение колебаний точки В относительно ее положения равновесия О/.
- Обозначим время от начала колебаний в О1до рассматриваемого момента черезt1,
- тогда отклонение точки Вчерез времяt1 после начала колебаний равно
![]() ,
,
однако t= t1, т.е.t1=t -
Тогда ![]() (2.1)
(2.1)
За время Тколебание распространилось на,
а за- на расстояние![]() ,
т.е.
,
т.е.
![]() (2.2)
(2.2)
Подставим (2.2) в
(2.1):
![]() (2.3)
(2.3)
Величина
![]() называетсяволновым числом,
называетсяволновым числом,![]()
тогда
![]()
- это уравнение волны, определяющее смещение любой точки В волнового фронта для любого момента времени t, отсчитываемого от момента возникновения колебания в начале О, по отношению к которому дана координата х точки В.
Уравнение волны, распространяющейся в сторону убывания х , отличается только знаком:
![]() .
.
Здесь
![]() фаза
точки В в момент t.
фаза
точки В в момент t.
В этот же момент времени фаза точки Мравнаt= 2t/T, тогда
![]()
называют разностью фаз колебаний в точках М и В.
Тогда уравнение волны (2.3) примет вид:
![]() .
.
Таким образом, ![]() 2.
2.
- путь волны в долях длины волны, запаздывание в долях периода и разность фаз в долях окружности выражаются одним и тем же числом.
Уравнение колебаний точкиВимеет вид:
![]() (2.5)
(2.5)
Дважды дифференцируем уравнение волны (2.3) по х, имеем
![]() (2.6)
(2.6)
Подставим(2.6) в (2.5):![]() учитывая,что
учитывая,что
![]()
получаем ![]() (2.7)
(2.7)
Это общее уравнение
волны, распространяющейся в направлении
Х.Оно связывает величины
![]() ,
х,t для любой точки
при прохождении волны через эту точку.
,
х,t для любой точки
при прохождении волны через эту точку.
Для волны,
распространяющейся в произвольном
направлении
![]() ,
уравнение волны имеет вид
,
уравнение волны имеет вид
![]()
где
![]() -лаплассиан
-лаплассиан ![]() .
.
Решение этого
уравнения![]() .
.
При выводе уравнения (2.3) мы предполагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в тех случаях, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны по мере удаления от источника уменьшается, следовательно, уменьшается и амплитуда - волна затухает.
В однородной среде такая волна описывается уравнением
![]() ,
,
где
![]() -амплитуда в точках плоскостиr=0.
-амплитуда в точках плоскостиr=0.
2. Теперь найдем уравнение сферической волны.
Всякий реальный источник волн обладает некоторой протяженностью. Однако на расстояниях r много больших размеров источника, последний можно считать точечным. В изотропной и однородной среде волна, распространяющаяся от точечного источника, будет сферической.
Пусть фаза колебанийисточника равна
 .
.Тогда точки, лежащие на волновой поверхности радиуса r,будут колебаться с фазой
![]()
Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, не остается постоянной – она убывает с расстоянием от источника по закону
![]() ,
,
поэтому уравнение
сферической волны имеет вид
![]()
где а -амплитуда колебаний на расстоянии 1м от источника.
Для поглощающей
среды![]()
Итак, скорость распространения волны есть скорость распространения колебательного процесса, не совпадающая со скоростью колебаний отдельных частиц среды, которые осуществляют этот процесс. Величина скорости зависит и от того, в каком направлении ее измерять.
Скорость
перемещения в пространстве точек
волновой поверхности, колеблющихся в
одной фазе, называетсяфазовой
скоростью волны
![]() (в рассматриваемых ранее уравнениях
(в рассматриваемых ранее уравнениях![]() – фазовая скорость)
– фазовая скорость)
Фазовая скорость поперечных волн в изотропной однородной среде
 ,
,
где модуль сдвига, - плотность среды.
Распространение продольных волнв тонком длинном стержне связанно с его продольным растяжением и сжатием,
фазовая скорость
таких волн![]() ,
гдеЕ –модуль Юнга для
стержня.
,
гдеЕ –модуль Юнга для
стержня.
