книги / Теория функций комплексного переменного

2. Общая показательная функция w = az является многозначной.

Обратные тригонометрические и гиперболические функции

Функции, обратные к тригонометрическим и гиперболическим функциям, определяются, как и в действительной области.

Например, число w называется арксинусом числа z, если sin w = z, и обозначается w = Arcsin z.

Аналогично определяются функции Arccos z, Arctg z, Arcctg z.

Поскольку функция sin z определяется через показательную функцию, то обратная к ней будет выражена через ло-

гарифм
w = Arcsin z = −i Ln (i z + 1− z2 ).	(4.17)

Функция w = Arcsin z многозначна.

Аналогично определяются остальные обратные тригоно-

метрические и функции								z2 +1),
Arccos z = −iLn (z +									(4.18)
Arctg z = −			i		Ln i − z		,	(z ≠ ±1),	(4.19)
	2					i + z
Arcctg z =		i			Ln	z −i	,	(z ≠ ±1).	(4.20)
						z +i
	2
Функции, обратные гиперболическим, обозначаются соот-
ветственно Arcsh z	(ареа-синус),							Arcch z	(ареа-косинус),
Arcth z (ареа-тангенс),	Arccth z (ареа-котангенс).

Обратные гиперболические функции имеют следующие выражения:

31

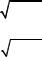
Arsh z = Ln (z +

z2 +1),

(4.21)

Arch z = Ln (z +

z2 −1),

(4.22)

Arth z =

1 Ln

1+ z

,

(4.23)

2

1− z

Arcth z =

1 Ln

z +1

.

(4.24)

2

z −1

Все эти функции многозначны.

Предел и непрерывность функции

комплексного переменного

Число

А

( А

) называют

пределом

функции

f (z)

в точке z0 ,

если для любого числа ε > 0 найдется число δ(ε),

такое, что

для

всех

z, удовлетворяющих

неравенству

0 <

z − z0

< δ(ε),

выполняется неравенство

f (z) − А

< ε:

lim f (z)

( ε > 0)( δ(ε))( z,

0 <

z − z0

< δ(ε)):

z→z0

f ( z) − A

< ε.

(4.25)

Существование предела lim f ( z) , где

z→z0

f (z) =u ( x, y) +iv(x,y),

z0 = x0 +iy0 ,

равносильно

существованию

двух

пределов

lim u ( x, y)

x→x0

y→y0

и lim v(x, y) , причем lim

f (z) = lim u (x, y) +i lim v(x, y) .

x→x0

z→z0

x→x0

x→x0

y→y0

y→y0

y→y0

Функция

f (z)

называется непрерывной в точке z0 ,

если

lim f (z) = f (z0 ) .

z→z0

32

Функция f (z) называется непрерывной в области G, если она непрерывна в каждой точке этой области.

Дифференцирование функции комплексного переменного

Пусть функция w = f (z)

определена в некоторой области

G комплексной плоскости. Пусть точки z и z +∆z

принадле-

жат области

G.

Пусть,

далее,

∆z = ∆x +i∆y,

∆w =

= f (z +∆z) − f (z).

Функция w = f (z)

называется дифференцируемой в точ-

ке z G,

если в этой точке существует конечная производная

f ′(z0 ) =

lim

∆f

(z0 )

= lim

f (z +∆z) − f (z)

.

∆z

∆z

∆z→0

∆z→0

Критерий дифференцируемости функции

Пусть z = x +iy ,

w = f (z) =u(x, y) +iv(x, y).

Функция

w = f (z)

дифференцируема в точке z G тогда и только тогда,

когда функции u =u(x, y) и v = v(x, y)

дифференцируемы как

функции действительного переменного в точке (x, y)

и в этой

точке выполняются условия Коши-Римана:

∂u

= ∂v ,

∂x

∂y

(4.26)

∂u

= −∂v .

∂y

∂x

С учетом условий Коши-Римана производную дифференцируемой функции f (z) можно находить по формулам

33

f ′(z) =	∂u	+i	∂v	,	f ′(z) =	∂v	+i	∂v	,
	∂x		∂x			∂y		∂x	(4.27)
f ′(z) =	∂u	−i	∂u	,	f ′(z) =	∂v	−i	∂u .
	∂x		∂y			∂y		∂y

Правила дифференцирования функций действительного переменного справедливы и для функций комплексного переменного, дифференцируемых в точке z.

Аналитическая функция

Функция w = f (z) называется аналитической в точке z G, если она дифференцируема в этой точке и некоторой ее окрестности.

Функция w = f (z) называется аналитической в области G, если она аналитична в каждой точке этой области.

Точки, в которых однозначная функция w = f (z) аналитична, называются правильными точками этой функции. Точки, в которых функция w = f ( z) не является аналитической,

называются особыми точками этой функции. Уравнение

∂2φ + ∂2φ = ∂x2 ∂y2 0

называется уравнением Лапласа. Функции, удовлетворяющие уравнению Лапласа, называются гармоническими функциями.

Достаточные условия аналитичности функции

Если гармонические в области G функции u =u (x, y) и v = v(x, y) связаны между собой условиями Коши-Римана, то функция f (z) =u (x, y) +i v(x, y) является аналитической в области G.

34

Пару гармонических функций u =u (x, y) и v = v(x, y),

связанных между собой условиями Коши-Римана, называют сопряженными. Пара сопряженных в области G функций со-

ставляют аналитическую функцию

f (z) =u (x, y) +i v(x, y).

Пример 4.5. Проверить, является ли функция

v(x, y) =

= ex sin y гармонической.

Найдем

частные

производные

функции

v(x, y):

∂v

= e

x

sin y ,

∂2v

= e

x

sin y ;

∂v

= e

x

cos y ;

∂2v

= −e

x

sin y . Так

∂x

∂x2

∂y

∂y2

как

∂2v

+

∂2v

= e

x

sin y −e

x

sin y

= 0 , то функция v(x, y)

являет-

∂x2

∂y2

ся гармонической.

Зная одну из сопряженных гармонических функций, можно восстановить другую с точностью до постоянного слагаемого.

Сопряженную гармоническую функцию можно восстановить с помощью условий Коши-Римана.

Пусть известна гармоническая функция u =u(x, y). Сопряженная ей функция v(x, y) может быть найдена с помощью криволинейного интеграла следующим образом: v(x, y) =

( x, y)	∂u	dx +	∂u	dy. В случае односвязной области	G этот
= ∫ −	∂y		∂x
( x0 , y0 )

интеграл не зависит от пути интегрирования.

На практике бывает проще использовать условия КошиРимана непосредственно.

Из первого условия Коши-Римана найдем функцию v(x, y) с точностью до постоянного относительно x слагаемого:

y	∂v	y	∂u	dy +ϕ(x).
v(x, y) = ∫	∂y	dy +ϕ(x) = ∫	∂x
y		y
0		0

35

Функцию ϕ(x) найдем с помощью второго условия Ко-

∂

y

∂u

∂u

ши-Римана:

∫

∂x

dy +ϕ(x) = −

∂y

.

∂x y

0

Аналогично по заданной гармонической функции v(x, y)

можно найти сопряженную ей функцию u(x, y).

Пример 4.6. Найти гармоническую функцию u(x, y), со-

пряженную к функции v(x, y) = ex sin y.

В силу первого условия Коши-Римана ∂u =

∂

(ex sin y) =

∂y

∂x

= ex cos y. Следовательно, u(x, y) =

x

∫ ex cos ydx +ϕ( y)

= ex cos y +

0

+ ϕ( y) .

Найдем производную функции u(x, y) по переменной y:

∂

∂

x

x

u(x, y) =

(e

cos y +ϕ( y)) = −e

sin y +ϕ′( y). В силу второго

∂y

∂y

x

∂v

∂

(e

x

sin y) =

условия Коши-Римана −e

sin y +ϕ′( y) = −∂x = −

∂x

= −ex sin y.

Таким образом,

ϕ′( y) = 0, следовательно,

ϕ( y) = c

и u(x, y) = ex cos y +c.

Условие f (z0 ) = с0 , где z0 , с0 – заданные числа, позволяет определить аналитическую функцию f (z) однозначно.

Пример 4.7. Восстановить аналитическую функцию f (z) по ее мнимой части v(x, y) = ex sin y и значению f (0) =1.

В силу примера 4.5. функция v(x, y) является гармонической. В силу примера 4.5 сопряженная функция имеет вид u(x, y) = ex cos y +c . Следовательно, w(x, y) = ex (cos y +isin) y +

36

+ c. Значит f (z) = ez +c. Из условия f (0) =1 вытекает, что с = 0. Итак, f (z) = ez .

Пример 4.8. Восстановить аналитическую функцию

f (z)

по ее действительной части u =

x

и значению

f (π) =

1 .

x2 + y2

π

Найдем

частные

производные функции

u:

∂u =

∂x

=

y2 − x2

∂u

=

−2xy

;

∂y

.

(x2 + y2 )2

(x2 + y2 )2

∂v

=

y

2

− x

2

,

∂y

(x2

+ y2 )

2

Тогда в силу условий Коши-Римана

∂v

2xy

=

.

∂x

(x

2

+ y

2

)

2

Интегрируя второе равенство по переменной

x, получим

v(x; y) =

−y

+ϕ( y).

Тогда

∂v =

y2 − x2

+ϕ′( y).

В

силу

x2 + y2

∂y

(x2 + y2 )2

первого условия Коши-Римана,

	ϕ( y) = c	и v(x; y) =	−y	+с.
			x2 + y2

ϕ′( y) = 0, следовательно,

	Отсюда f (z) =	x	−
		x2 + y2

	−i	y		+ic.		Так как x −iy = z и	x2 + y2 = zz , то
		x2 + y2
	f (z) =		1 +ic.		Из условия f (π) = 1 следует, что c = 0. Поэтому
			z			π
	f (z) =		1 .
			z
		Замечание.				Аналитическую функцию	f (z) можно вос-

становить по одной из формул:

37

f (z) = 2u		z + z0		,		z − z0				−c ,
		2					2i			0
f (z) = 2iv			z + z0		,		z − z0			+c ,
		2					2i			0

где c0 – сопряженное число для c0 = f (z0 ), z0 – сопряженное число для z0.

Пример 4.9. Восстановить аналитическую функцию f (z)

по ее мнимой части v(x, y) =3x +2xy

и значению f (i) = 2.

Воспользуемся формулой

f (z) = 2iv

z + z0

,

z − z0

+c .

2

2i

0

Получим:

f (z) = 2i

3

z −i

+2

z −i

z +i

+2 = z2 +3iz +6.

2

2

2i

Конформные отображения

Сформулируем самое общее определение конформного отображения.

Определение 1. Непрерывное отображение, сохраняющее форму бесконечно малых фигур, называется конформным.

Уточним определение 1. Пусть										– комплексное евкли-
дово пространство,	f : →					– непрерывное					отображение,
определенное на области G .
Будем говорить, что отображение w = f (z)											обладает свой-
ством постоянства растяжений в точке										z0 G, если существует
конечный предел lim			f (z) − f (z0 )						= k. Число k = k (z0 , f ) на-
				z − z0
z→z0

зывается коэффициентом растяжения в точке z0. 38

Отображение w = f (z) обладает свойством сохранения углов в точке z0 G, если любая пара непрерывных кривых l1 и l2 , расположенных в области G и пересекающихся в точке z0 под углом α при рассматриваемом отображении, переходит в пару непрерывных кривых L1 и L2 , пересекающихся в точке w0 = f (z0 ) под те же углом α.

Определение 2. Непрерывное отображение w = f (z) области G комплексной области называется конформным в точке z0 G, если оно обладает свойствами постоянства растяже-

ний и сохранения углов.

Определение 3. Непрерывное отображение области G называется конформным, если оно конформно в каждой точке этой области.

	Критерий конформности отображения
Отображение w = f (z)							является конформным в области
G комплексной плоскости тогда и только тогда, когда функ-
ция f (z)	аналитична в области G и f ′ (z) ≠ 0 при всех z G.
Таким образом, если в точке								z0 G существует отличная
от нуля производная f ′ (z0 ) ≠ 0,								то каждый бесконечно малый
вектор с началом в точке z0							при отображении w = f (z)			растя-
гивается	в	k =		f ′ (z0 )			раз,	поворачивается	на	угол
α = arg f ′ (z0 )		и параллельно сдвигается на вектор							f (z0 ) − z0 ;

бесконечно малые круги переходят в бесконечно малые круги.

Линейное отображение

Пусть a,b , a ≠ 0. Отображение, осуществляемое линейной функцией

39

w = az +b,

(4.28)

называется линейным отображением. Линейное отображение является конформным не всей комплексной плоскости, так как w′ = a ≠ 0.

Частные случаи:

1) w = z +b – преобразование параллельного переноса; 2) w = eiα z (α R) – преобразование поворота вокруг на-

чала координат на угол α;

3) w = rz (r R, r > 0) – преобразование подобия с центром в начале координат и коэффициентом подобия r.

Общий случай w = az +b, где a = reiα – преобразование, осуществляемое путем последовательного применения 1) поворота вокруг начала координат на угол α; 2) преобразования подобия с центром подобия в начале координат и коэффициентом подобия r; 3) параллельного переноса с помощью вектора, соответствующего комплексному числу b.

Дробно-линейное отображение

Дробно-линейным называется отображение с помощью функции

	w =	az +b	,	(4.29)
		cz +d

где a,b,c, d и ad −bc ≠ 0.

Дробно-линейная функция взаимно-однозначно и конформно отображает расширенную комплексную плоскость Z на расширенную комплексную плоскость W.

Дробно-линейное преобразование может быть получено с помощью последовательного применения линейных преобра-

зований и преобразования вида w = 1z .

40