37. Неявные функции, теорема об обратной функции. Не будет в экзе!!!

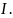Функция одной переменной

F(x, y) = 0 (1)

Если для каждого

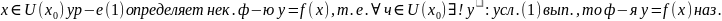
неявной ф-й, заданной в .

Теорема 1:

Пусть

F(x, y) = 0 (1)

F: 1) F( )=0

2) непр. в U( )

3)Имеет непрер. част. произв. в U( )

4) 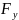( ) != 0

P( )

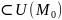
В U( ) ур-е (1) определяет неявную ф-ю со значениями в U(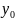 ), причём

1. 

2. f(x) непр. в U( )

3. в т. (x, f(x)) в U( )

II. Неявные функции нескольких переменных

F(

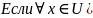
Теорема:

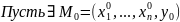
F

1. F( )=0

2. Непрер. в U( )

3. Имеет частную непр. произв. в U( )

4. 

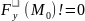
Тогда 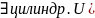) со значениями в

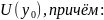
а) f( )=

б) f непр. в U( )

в) 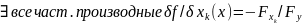в U( ) и непрер.

III. Матрица Якоби, Якобиан

Матрица Якоби - Матрица частных производных

Якобиан - определитель матрицы Якоби

IV. Система неявных ф-й

Условие:

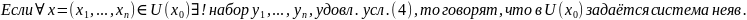
функций.

Теорема:

1. 

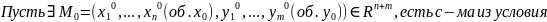
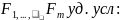
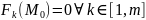
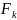2. непр. в U( )

3)все ф-и им. непр. частные произв. по всем переменным в U( )

4) ) /

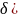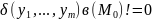
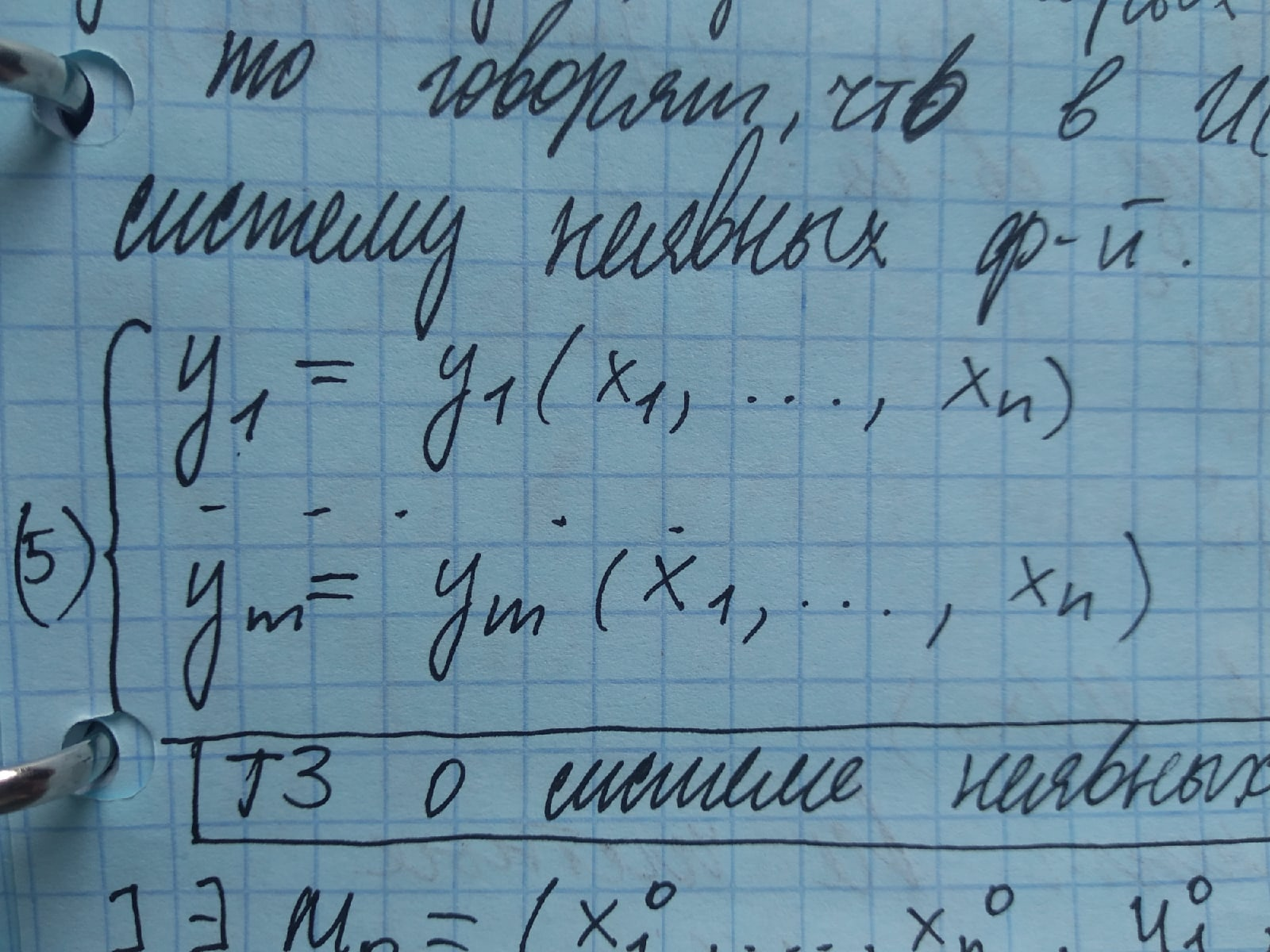
т. ч. ) 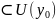, причём выполняются след. св-ва:

1. 

2. 

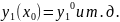
3. ф-и имеют все част. произв., непр. в

38. Условные экстремумы, метод множителей Лагранжа.

f(x₁, …, x_n) определена в D Rⁿ

1. ⎧ -уравнение связывающее переменные

…

⎨

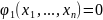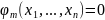⎩ -уравнение связи

При этом m<n

Возьмем (.) x₀ = ( D, удовлетворяющую (1)

Определение: x₀ - (.) условного максимума функции f при условиях (1), если 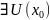: 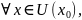x удовлетворяет (1), f(x) f(x₀)

x₀ - (.) условного минимума функции f при условиях (1), если : x удовлетворяет (1), f(x) f(x₀)

Метод множителей Лагранжа

Функция L(x, ) = f(x) + 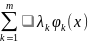- функция Лагранжа

x = (x₁, …, x_n)

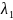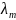= ( , …, ) - множители Лагранжа

Теорема 1: необходимое условие условного экстремума

Пусть f, удовлетворяет условиям:

1. непрерывна в D

2. имеют непрерывные частные производные в D

3. 0 в D, (Якобиан; берем последние n “иксов”)

x₀ - (.) условного экстремума функции f

Тогда набор 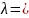, …, ), так что все частные производные

= 0 (2)

Теорема 2: достаточное условие условного экстремума

Пусть f, удовлетворяет тем же условиям, что и в первой теореме и они являются дважды непрерывно-дифференцируемы в U(x₀), x₀ удовлетворяет условию (2)

Если d²L(x₀, ) > 0, при выполнении условий (1), то х₀ - (.) условного минимума

Если d²L(x₀, ) < 0, при выполнении условий (1), то х₀ - (.) условного максимума (маленький бонус)