Решение. Согласно формуле Стокса

Тогда

P(x, y, z) = x2 y3 ,

Q(x, y, z) =1, R(x, y, z) = z.

∂Q

∂P

∂R

∂Q

∂P

∂R

−

= −3x

2

y

3

,

−

= 0,

−

= 0.

∂x

∂y

∂y

∂z

∂z

∂x

И по формуле Стокса получаем

∫x2 y3dx + dy + zdz = −3∫∫x2 y2dxdy = −3∫∫x2 y2dxdy =

L

S

D

1

2π

1

3 ∫(1

ρ

2

= −3 ∫dϕ∫ρ2 cos2 ϕ ρ2 sin2 ϕ ρdρ = −

−cos2 2ϕ)dϕ

=

6

0

0

4

0

2π

= −1

2π

1 (1 +cos 4ϕ))dϕ = −

1

(ϕ

− sin 4ϕ)

π .

∫ (1−

= −

8

0

2

8

2

8

0

8

#

5. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

5.1. Скалярные и векторные поля.

Если с каждой точкой

M (x, y, z) определенной пространственной области (которая может охватывать и все пространство) связана некоторая скалярная или векторная величина, то говорят, что задано поле этой величины,

соответственно скалярное или векторное.

Примером скалярного поля может служить поле температуры или

электрического потенциала. Так как положение точки M координатами, то задание поля скалярной величины U

определено ее равносильно

заданию числовой функции U (x,y,z), которая предполагается непрерывной вместе со своими частными производными первого порядка.

Примером векторного поля может служить силовое поле или поле

скоростей. Задание поля векторной величины a может быть осуществлено путем задания ее проекций на оси координат

ax(x, y, z), ay(x, y, z), az(x, y, z)

(5.1)

как функций от координат точки M, с которой величина вектора a связана. Эти функции предполагаются непрерывными вместе со своими частными производными первого порядка.

5.2. Градиент. Пусть задано скалярное поле U (x,y,z). Введем вектор g , с координатами

43

∂∂Ux , ∂∂Uy , ∂∂Uz .

Этот вектор называют градиентом величины U и обозначают

g = gradU .

Градиент по числовому значению и по направлению характеризует наибольшую скорость изменения величины U . Причем направление градиента совпадает с направлением нормали к поверхности уровня U (x, y, z) = c , проходящей через данную точку.

Итак, скалярное поле U (x, y, z) порождает векторное поле градиента gradU .

5.3. Поток векторного поля через поверхность. Формула Остроградского. Дивергенция. Пусть задано векторное поле a(M ) , то

есть заданы три функции (5.1) и
		(x, y, z) = ax (x, y, z)				+ ay (x, y, z)		+ az (x, y, z)		.
	a				i		j		k		(5.2)
Возьмем поверхность S и, выбрав определенную ее сторону,
обозначим			через	cos α, cosβ, cos γ				направляющие			косинусы

соответственно направленной нормали n к поверхности S. Тогда поверхностный интеграл

∫∫(ax cosα +ay cos β + az cosγ )ds	(5.3)
S

называется потоком векторного поля a через поверхность S в указанную сторону и обозначается П.

Если вектор a определяет поле скоростей текущей жидкости, то интеграл (5.3) выражает количество жидкости, протекающей через

поверхность S за единицу времени.

Используя связь между криволинейными интегралами первого и

второго типа, потоку П вектора a через поверхность S можно придать другое выражение

П = ∫∫(ax cosα +ay cos β + az cosγ )ds = ∫∫axdzdy +aydxdz + az dx .

S S

Рассмотрим тело V , ограниченное замкнутой поверхностью S; через n обозначим внешнюю нормаль к поверхности. Тогда по формуле Остроградского (4.10), если положить в ней P = ax , Q = ay R = az,

можно выражение потока вектора a через поверхность S преобразовать в тройной интеграл

∫∫	axdydz + aydxdz + az dxdy =	∫∫∫	(	∂a		∂ay	+	∂a		(5.4)
				∂x		∂y		∂z
S		V			x +				z )dxdydz.

44

Выражение, стоящее под знаком тройного интеграла, называется

дивергенцией (или расходимостью) вектора a и обозначается

∂a

x

∂ay

∂a

z

div a =

+

+

.

(5.5)

∂y

∂x

∂z

Дивергенция есть скаляр, который можно поставить в соответствие каждому вектору a . Следовательно, векторное поле a порождает скалярное поле дивергенций div a .

Если div a (M0) > 0, то точка M0 называется источником, если div a (M0) < 0, то точка M0 называется стоком. Абсолютная величина

div a (M0) характеризует мощность источника или стока.

Векторное поле, во всех точках которого дивергенция равна нулю,

называется соленоидальным. Поток соленоидального поля через любую замкнутую поверхность равен нулю.

Пример 5.1. Дано векторное поле :

a = (x − 2z)i + (3z − 4x) j + (5x + y)k .

Найти дивергенцию поля a в точке M0(0, 1, 2) и, с помощью

формулы Остроградского, поток поля a через полную поверхность треугольной пирамиды, заданной плоскостями x + y + z = 2, x = 0, y = 0, z = 0(через внешнюю сторону поверхности).

Решение. Дивергенцию векторного поля a найдем по формуле

	(5.5)			∂								∂														∂
	div		=		(x − 2z) +										(3z − 4x) +													(5x + y) =1 + 0 + 0 =1.
		a
												∂y
				∂x																						∂z
	В любой						точке				пространства														div				= 1.				Согласно											формуле
																												a
	Остроградского,
																									2							2−x	2−x−y
				П = ∫∫∫diva									=∫∫∫dxdydz												= ∫dx ∫ dy										∫dz =
							V								V										0							0			0						2−x
				2			2−x																	2										y2
																																− x) y −												=
				= ∫dx ∫(2 − x − y)dy == ∫dx (2																															2
				0				0																0																	0
						2																										1
														2				(2 − x)2											1						2
								(2 − x)							−																	∫(2 − x)					dx =
					= ∫																2			dx =					2
						0																										0
						1			(2	− x)3										1		1		((2 −1)							3					3		)=				7
				=																	= −											−(2 −0)											.	#
						2	−			3												6																				8
																				0

45

5.4. Циркуляция вектора. Формула Стокса. Вихрь. Пусть задано векторное поле a (M)

a(x, y, z) = ax (x, y, z)i + ay (x, y, z) j + az (x, y, z)k .

Интеграл ∫axdx + ay dy + az dz , взятый по некоторой кривой L,

L

называется линейным интегралом от вектора a вдоль кривой L. Если

поле a есть силовое поле, то линейный интеграл выражает работу сил поля при перемещении точки по кривой L. В случае замкнутой кривой

этот интеграл называют циркуляцией вектора	a	вдоль кривой L и
обозначают
Ц = ∫axdx + aydy + az dz.		(5.6)

L

Пусть замкнутый контур L ограничивает некоторую поверхность S.

Тогда по формуле Стокса (4.11) циркуляция вектора a вдоль этого контура может быть выражена поверхностным интегралом

Ц = ∫axdx + aydy + azdz =

∂a

∂ay

L

∂a

∂a

∂ay

∂a

= ∫∫(

z

−

)dydz +(

x

−

z

)dxdz +(

−

x

)dxdy . (5.7)

∂y

∂z

∂x

S

∂z

∂x

∂y

Вектор с проекциями на оси Ox , Oy ,

Oz соответственно

∂a

z

−

∂ay

,

∂a

x

−

∂a

z

,

∂ay

−

∂a

x

∂y

∂z

∂z

∂x

∂x

∂y

называется вихрем или ротором вектора a и обозначается rot a .

Формула (5.7) показывает, что циркуляция вектора вдоль замкнутого контура равна потоку вихря через поверхность, ограниченную этим контуром. При этом направление обхода контура и сторона поверхности должны соответствовать друг другу.

Заметим, что векторное поле a порождает векторное же поле

вихря rota .

Пример 5.2. С помощью формулы Стокса найти циркуляцию векторного поля a = yi − x j + 2k вдоль окружности x2 + y2 =1, z = 0 .

Решение. Из задания векторного поля a следует, что

ax = y , ay = −x , az = 2 .

Тогда

∂ay

∂a

∂ay

∂a

∂a

z

−

= 0,

x

−

∂a

z

= 0,

−

x

= − 2

∂z

∂x

∂x

∂y

∂z

∂y

и, согласно формуле (5.7), имеем

46

Ц = ∫∫(−2)dxdy = −2 ∫∫dxdy .

S	S xy
Sxy – проекция поверхности S на	xOy и представляет собой круг с

центром в начале координат и радиусом равным 1. Перейдя в двойном интеграле к полярным координатам (см. пункт 1.4) , получим

	2π	1	2π	1
Ц = −2 ∫∫dxdy = −2 ∫dϕ∫ρdρ = −2 ∫					dϕ = −2π.
				2
S xy	0	0	0
							#
		Векторное поле, во всех точках
	которого		вихревой			вектор	равен
	нулю,называется				потенциальным		или
	безвихревым. В потенциальном поле линейный
	интеграл (работа) не зависит от формы линии,
	соединяющей какие-либо две его точки, а
	циркуляция всегда равна нулю.
		Потенциал U (x, y, z) такого поля
	определяется по формуле
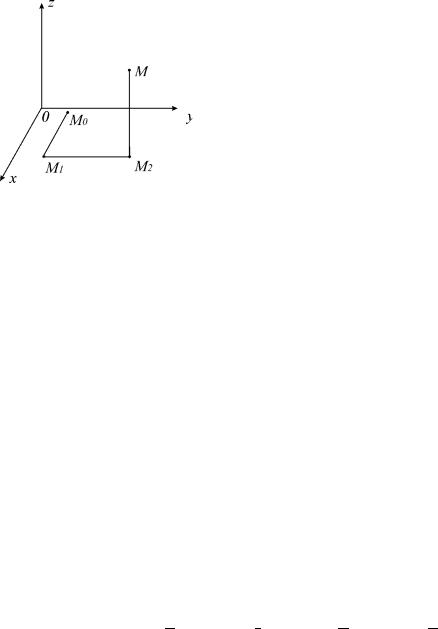
Рис. 5.1			M
	U (M ) =		∫axdx + ay dy + az dz,				(5.8)
			M 0

где интеграл берется по любому пути, исходящему из некоторой

фиксированной точки	M 0 (x0 , y0 , z0 ) .	Обычно	в качестве такого пути
выбирают ломаную M 0M1M 2M , состоящую из отрезков прямых,
параллельных осям координат (рис. 5.1). Точки ломаной				M 0M1M 2M
имеют следующие	координаты:	M 0 (x0 , y0 , z0 ) ,		M1(x1, y1, z1) ,
M 2 (x2 , y2 , z2 ) , M (x, y, z) В этом случае имеем			y
	x
U (M ) =U (x, y, z) = ∫ax (x, y0 , z0 )dx + ∫ay (x, y, z0 )dy +
	x0		y0
	z
	+ ∫az (x, y, z)dz .			(5.9)

z0

Векторное поле, являющееся одновременно и соленоидальным и потенциальным, называется гармоническим.

Пример 5.3. Проверить, является ли векторное поле a = (z + y)i + (x + z) j + (x + y)k

соленоидальным и потенциальным. Если поле является потенциальным, то найти его потенциал.

47

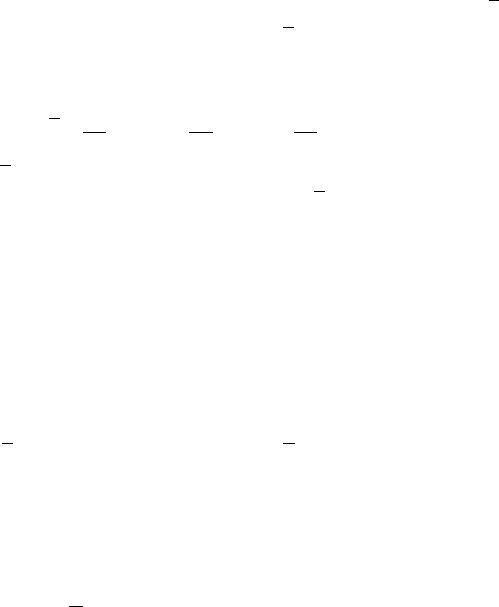
Решение. Чтобы ответить на вопрос, является ли поле a

соленоидальным, найдем дивергенцию вектора a .Так как

ax = z + y, ay = x + z, az = x + y ,

то по формуле (5.5) найдем дивергенцию поля

diva = ∂∂x (z + y) + ∂∂y (z + x) + ∂∂z (x + y) = 0,

значит поле a соленоидальное.

Чтобы ответить на вопрос, является ли поле a потенциальным,

найдем ротор вектора

a

rot

a

:

i

j

k

rot

=

∂

∂

∂

a

=

∂x

∂y

∂z

y + z

x + z

x + y

=

∂

∂

+

∂

∂

∂

∂

= 0.

i

j

+

∂x

∂y

k

∂y

∂z

∂z

∂x

x + z x + y

x

+ y y + z

y + z x + z

Значит поле a потенциальное. Потенциал поля a найдем по формуле (5.9), приняв за точку M0 (x0 , y0 , z0 ) точку начала координат O(0,0,0). Тогда

			x			y	z
U (M ) =U (x, y, z) = ∫0dx + ∫xdy + ∫(x + y)dz =
			0			0	0
= xy		y + (x + y)z			z	= xy + xz + yz
		0			0

есть потенциал поля a .

#

48