4 курс / Лучевая диагностика / ТОМОГРАФИЧЕСКИЕ_ИЗМЕРИТЕЛЬНЫЕ_ИНФОРМАЦИОННЫЕ_СИСТЕМЫ

∞ ∞
μх (х, у) = ∫ ∫ Zα (x −ξ, y −η)Sδ (ξ,η)dξdη,	(2.130)

−∞ −∞

∞

где Zα (r ) = ( 1 )3 ∫ ν 2 J0 ( ν2 (r )d ν 4 ) , r = (х2 + у2 )12 , 2π 1+ α(δ) ν 1+ ν

0

ν= (ν12 + ν22 )12 , J0 (u) – функция Бесселя нулевого порядка. Далее необходимо выбрать параметр регуляризации α(δ) так,

чтобы μα(δ) → μ0 при δ → 0 .

Рассмотрим некоторые моменты численной реализации регулирующего алгоритма, например, с выбором α по невязке. Заметим, что выражение (2.130) представляет собой свертку функции Zα (r )

с функцией Sδ (x, y) . Поэтому при проведении вычислений можно воспользоваться теоремой о свертке, т. е. вместо (2.130) использо-

вать эквивалентную ей форму.

μα (ν1,ν2 ) = Zα (

ν

) Sδ (ν1,ν2 ) ,

(2.131)

Zα (

ν

) =

1

ν

,

(2π)

2 (1+

4

+1)

1+ α(δ)

ν

ν

ν

= (ν12 + ν22 )1 2 ,

где Sδ (ν1,ν2 ) – фурье-образ функции Sδ (x, y) ;

μα (х, у) – фурье-

образ регуляризированного решения μα (х, у) .

При численной реализации (2.131) основными операциями являются дискретное прямое и обратное преобразования Фурье.

Остановимся на вопросе вычисления функции Sδ (x, y) , имеющей вид

π
Sδ (x, y) = ∫Рδ (хcos θ + y sin θ,θ)dθ.	(2.132)
0
171

Поскольку измерения функции Pδ (l, θ) проводятся для конечного числа углов θ [0, π] и в узлах lK = −R0 + (K −1) l ( l = 2R0 (N −1), K =1,2,..., N ), то R0 – радиус исследуемого объек-

та для параллельной схемы сканирования. При замене (2.132) какойлибо квадратурной формулой надо осуществлять интерполяцию

функции Pδ (l, θ) . Обычно используют метод интерполяции по бли-

жайшим точкам или метод линейной интерполяции. Однако эти методы интерполяции могут не обеспечить наилучшего порядка погрешности приближения дажев классе кусочно-непрерывных функций.

От этих недостатков свободны интерполяционные сплайны n-го порядка, т. е. функции θδ(n) (x, y; θ) , имеющие непрерывные про-

изводные по х, у до n-го порядка и совпадающие с Pδ (lK , θ) для каждого фиксированного θ [0, π] в узлах lK .

Аппроксимируя интеграл (2.132) какой-либо квадратурной формулой и заменяя функцию Pδ (l, θ) интерполяционным сплайном

Qδ(n) (x, y; θ) n-го порядка, получим формулу для приближенного нахождения функции Sδ (x, y) :

J
Sδ (x, y) = ∑a j Qδ(k ) (x, y; θj ) ,	(2.133)

i=1

где a j – коэффициент квадратурной формулы.

Можно ли построить регуляризирующие алгоритмы для уравнения (2.129), в которых не используются итерационные методы? На этот вопрос имеется положительный ответ [11]. Такие алгоритмы можно построить, основываясь на дополнительной информации об искомом решении (2.129).

Изложим подход по построению регуляризирующего алгоритма с использованием дополнительной информации об искомом решении на примере. Пусть модель исследуемого объекта истинного

значения μ0 (x, y) имеет вид

172

	С , R ≤				x2 + y2 ≤ R
	0			1			0
	С ,			x2 + y2 < R
	1,						1
				...
μ0 (x, y) =
С ,				(x, y)	C , i = 2,3,..., N −1
	i				i
				...
	C	N	, (x, y) C			N	,

где Ci – круг радиуса Ri , расположенный внутри кругов C1 C0 с радиусами R1 и R0 соответственно. В примере были взяты следующие параметры модели: R0 = 120 мм, R1 = 110 мм, C0 = 1000 Hv (Hv – величины Хаунсфилда), C1 = 0 Hv и x0 = x1 = 0 , y0 = y1 = 0 ,

где (xi , yi )		– центры кругов Ci . Остальные значения параметров
модели указаны в табл. 2.1.
							Таблица 2.1
				Параметры модели
							Ci , Hv
	i		xi , мм		yi , мм	Ri , мм
	2		0		44,5	5,5	–20
	3		0		0,0	24,0	–20
	4		48		0,0	52,0	–20
	5		68		–56,0	22,0	–50
	6		0		28,0	4,0	100
	7		0		36,0	3,0	100
	8		0		48,0	2,5	100
	9		0		60,0	2,0	100
	10		0		72,0	1,5	100
	11		0		84,0	1,0	100
	12		–22		–80,0	4,0	–100
	13		–11		–80,0	3,0	–100
	14		0		–80,0	2,0	–100
	15		11		–80,0	1,5	–100
	16		22		–80,0	1,0	–100

173

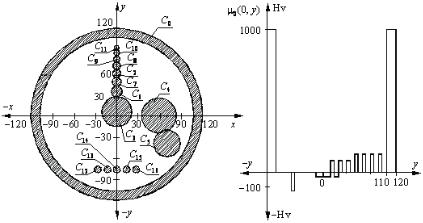
На рис. 2.24 показана модель исследуемого объекта и график функции μ0 (0, у) .

а

б

Рис. 2.24. Модель исследуемого объекта (а) и график функции μ0 (0, у) (б)

Под «тонкой структурой» функции μ0 (х, у) будем понимать функцию μ0 (х, у) с областью определения, включающей круги Ci

при i = 2, 3, 6, 7, 8, 9, 10, 11.

Для указанной модели μ0 (х, у) исследуемого объекта вычисля-

лись интегралы Р(l, θ) = ∫ μ0 (x, y)dl , где L(l, θ) – прямая ли-

L(l, θ)

ния с нормальными координатами (l, θ) из семейства прямых, инвариантного относительно вращения вокруг центра круга C0 , в ко-

торые вводилась случайная ошибка по формуле

Р(l, θ) = P(l, θ) + δ X P(l, θ)C , θ (0,π),

где X – равномерное распределение чисел в диапазоне [0, 1]. Уровень погрешности δ брался равным 0,005, что соответствует

средним значениям компьютерного томографа РКТ-01.

174

Для построения приближенного решения μ(х, у) основного уравнения КТ

Tμ ≡ ∫ μ(x, y)dl = P (l, θ)	(2.134)
L(−l, θ)

использовался регуляризирующий оператор Rgδ вида (2.124′). При

использовалась дополнительной информации об искомом решении

μ0 (х, у) .

Из табл. 2.1 видно, что

μ0 (х, у) = μ(х, у) + μ1 (x, y) ,

где

С0

, R1 ≤

x

2

+ y

2

≤ R0

x

2

+ y

2

< R

μ(х, у) =

, μ

(x, y) =

0,

i .

1

C ,

(x, y) C

0,

x

2

+ y

2

< R1

i

i

Вследствие непрерывности оператора T в (2.134) имеем

P(l, θ) = P (l, θ) + P1 (l, θ) θ [0, π],

где		(l, θ) = ∫ μ(x, y)dl ,	P1 (l, θ) = ∫ μ1 (x, y)dl , причем
	P
		L(l, θ)	L(l, θ)

функция P(l, θ) известна, функция P1 (l, θ) мала по сравнению с функцией P (l, θ) .

Это типично, например, для томографии головного мозга человека, когда функция μ(x, y) описывает распределение линейного коэффициента ослабления рентгеновского излучения в костных тканях человека, функция μ1 (x, y) – распределение этого коэффициента в веществе мозга. Так как костные ткани головы имеют постоянный коэффициент ослабления, то функция μ(x, y) всегда известна и много больше функции μ1 (x, y) .

Это позволяет приближенное решение искать в виде

π	+∞
μg (x, y) = ∫dθ ∫ Kg (l −l ') P(l ', θ) dl,		(2.134′)
0	−∞
	175

K (−ν)

где Kg (l, θ) = F −1

,

F −1 – оператор обратного

K (ν)

2 + g (ν,δ)

преобразования Фурье;

K (ν)

=

ν

−1 ,

а в качестве

g (ν,δ) взята

функция (2.124′′)).

На рис. 2.25 показаны графики функций μ0 (x, y)

и μg (x, y) для

«тонкой структуры»

при

x = 0 . Значения μg (x, y)

показаны для

g (ν,δ) = αδ(νp +1)2 ,

p = 2; α – выбрано по невязке, α = 0,06 .

Hv

μy (0, y)

μ0 (0, y)

100

0 y (расстояние)

−20 −Hv

Рис. 2.25. График функции «тонкой структуры» модели μ0 (0, y) и функции

μg (0, y) , полученной с помощью регуляризированного решения

Из рис. 2.25 видно, что регуляризированное решение достаточно хорошо описывает «тонкую структуру» решения μ0 (x, y) .

176

2.4.Анализ технических задач проектирования рентгеновских компьютерных томографов

2.4.1. Общие требования к рентгено-оптическому тракту

Полученные в пп. 2.1 и 2.2 результаты анализа и исследования физических проблем компьютерной томографии позволяют сформулировать общие требования к проектированию томографов.

Теория взаимодействия рентгеновского излучения с объектом, а также экспериментальные данные для основных компонентов живого организма (Н2О, Са) позволяют определить эффекты и явления, которые необходимо учитывать при создании томографических систем и задании требований к ним.

В первую очередь проводится анализ геометрии распространения излучения в исследуемом объекте: прямолинейное, криволинейное (рассеянное), соотношение прямолинейного и рассеянного излучений. Исходя из этого строится физическая геометрия сканера: параллельная схема сканирования, или веерная, или другая. Определяется стратегия детектирования: один детектор, множество детекторов, схема их калибровок. Разрабатывается алгоритм реконструкции изображения: для прямолинейного распространения рентгеновского луча или с учетом нелинейности его распространения (рассеяния и диффузии).

Решение уравнения переноса излучения достаточно точно определяет геометрию их распространения от источника излучения до блока детектирования. В зависимости от диапазона энергии фотонов, испускаемых источником излучения, составляющая рассеянного излучения на выходе из объекта исследования может составлять различные значения. Для диапазона энергий 17–150 кэВ, который выбирается исходя из принципа «полупрозрачности», высокого контраста мягких (Н2О) и костных (Са) тканей человека, минимальной дозы облучения, на исследуемом фантоме человека (Н2О) диаметром 30 см составляет около 3 % от прямолинейно распространяемых фотонов для неколлимированного пучка. Эта доля рассеянного излучения достаточно высока, чтобы реконструировать

177

изображение с «шумом» не более 0,5 %, что требуется для томографических систем.

Для уменьшения доли рассеянного излучения необходимо использовать точечный источник излучения с коллимацией луча как в плоскости сканирования, так и в плоскости, перпендикулярной плоскости сканирования. Более того, эти условия создания геометрии рентгеновского луча определяют также требуемое физическое приближение решения уравнения переноса с учетом дополнительного условия – моноэнергетического источника излучения. В сумме эти условия дают возможность найти приближенные решения уравнения переноса и с помощью этого приближения решить уравнение КТ при практической реализации. Практическая реализация заключается в установлении «лучевых сумм» вдоль прямолинейного распространения рентгеновского луча, представлении этих «сумм» в виде проекции, равной логарифму отношения измеренной интенсивности на входе и измеренной интенсивности на выходе исследуемого объекта.

Необходимо отметить, что если бы преобладала криволинейная (рассеянная) составляющая излучения, то вопрос создания рентгеновского компьютерного томографа до сих пор был бы открытым, так как решение уравнения переноса (например, для лазерного излучения или СВЧ-излучения, где преобладает рассеянная (дифракционная) составляющая), для создания этих видов томографов в настоящее время не найдено. Исходя из физического приближения решения уравнения переноса для рентгеновского луча идеальной схемой сканирования является использование точечного моноэнергетического коллимированного в двух плоскостях источника излучения с единичным детектором. Эта схема исключает влияние рассеянного излучения, но при этом осуществляется параллельновращательное движение системы источник–детектор: параллельное движение – для набора дискретных значений единичной проекции, вращательное – для набора дискретных ракурсов.

	Здесь калибровка соотношения	ln	J0i	= P(li , θj ) есть проекция,
			Jxi

при фиксированном угле θj выполняется идеальным образом для единичной проекции, так как измерение J0i (входной интенсивности из-

178

лучения перед объектом исследования) и Jxi (выходной интенсивности после объекта исследования) для единичной проекции проводится одним и тем же детектором. Это исключает влияние аддитивных и мультипликативных ошибок измерения детекторной системы и всего рентгено-оптического тракта преобразования измеряемого сигнала.

Учитывая, что параллельная схема сканирования является мало производительной, возможно использование веерной схемы с вращательным движением системы источник–детектор. Здесь используется множество единичных детекторов, и поэтому влиянием рассеянного излучения в объекте исследования здесь пренебрегать нельзя. Уменьшение влияния рассеянного излучения на качество изображения в этой схеме сканирования можно достичь конструктивным и алгоритмическим путем. В первом случае – это использование коллимированных ионизационных детекторных камер с достаточно большими в длину по направлению излучения катодными стенками из тяжелых (с большим Z) металлов (тантал, вольфрам, свинец). Если используется полупроводниковые детекторы (они имеют, как правило, достаточно малую длину в направлении излучения), то на окно детекторной линейки можно установить сетку-коллиматор с входным окном, равным входному окну единичного детектора.

Во втором случае используется корректировка соотношения ln J0i Jxi путем введения дополнительного соотношения в лога-

рифм (в проекцию), которое учитывает распределение рассеянного излучения вдоль слоя сканирования (вдоль длины линейки детекторов).

Как было показано выше, физическое приближение решения уравнения переноса для рентгеновской томографии имеет место только для точечного моноэнергетического коллимированного (в двух плоскостях сканирования) источника излучения. Из этого вытекают общие требования и к источнику рентгеновского излучения. Он должен иметь малое фокусное пятно (в идеале точку) излучения. Если источник применяется полиэнергетический, например, рентгеновская трубка, то на выходе источника должен стоять коллиматор в виде медной или алюминиевой пластины, сужающий первичный спектр излучения до достаточно узкого спектра. Если источник применя-

179

ется моноэнергетический, например, изотопный источник С060, то первичного коллиматора ставить не требуется.

Для создания узкого пучка в двух плоскостях для параллельной схемы сканирования и узкого веерного (слойного) пучка в одной плоскости для веерной схемы требуется соответствующий вторичный коллиматор, определяемый данную геометрию выходного пучка.

Если учитывать, что при практическом проектировании томографических систем по критерию вес – размеры – мощность, как правило, используются источники излучения, основанные на принципе облучения тяжелой мишени электронами (рентгеновские трубки, бетатроны, линейные ускорители), т.е. полиэнергетические источники рентгеновского излучения, то при переносе излучения в исследуемом объекте на выходе происходит ужесточение рентгеновского пучка, т.е. смещение спектра в сторону высоких энергий по отношению к входному спектру. Этот эффект приводит к нелинейности в определении томографического параметра μ – линейного коэффи-

циента ослабления, который зависит от E – энергии фотонов. Эта нелинейность выражается в виде нелинейного уменьшения значения μ с увеличением толщины (расстояния от периферии до цен-

тра) исследуемого объекта. И здесь требуется корректировка проекции с целью уменьшения влияния полихроматичности. Корректировка проекции проводится в виде изменения соотношения J0i/Jxi в логарифме или введением дополнительного соотношения в логарифм на основании расчетных моноэнергетических «лучевых сумм» для сплошного водяного фантома человека и экспериментальных калибровочных данных на фантоме реальных полиэнергетических «лучевых сумм».

Суть корректировки полихроматичности должна заключаться в таком видоизменении рабочей проекции ln J0i Jxi , которое бы приводило к μ = const , на всем изображении томограммы (и в центре, и на

периферии) и значение которого бы соответствовало некоторой эффективной энергии фотонов, которая бы определяла соотношение

∫μ(Eэф)dl =∫μ(E)dl , где левый интеграл – лучевая моноэнергети-

L L

180