
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
6. Линейные операторы и их свойства
Пусть
заданы линейные пространства X
и
Y.
Правило, по которому каждому элементу
 ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент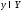 ,
называетсяоператором,
действующим в линейных пространствах
X,
Y.
Результат действия оператора A
на
элемент x
обозначают
Y
= A
x
или Y
= A
(x).
Если элементы X
и Y
связаны соотношением
,
называетсяоператором,
действующим в линейных пространствах
X,
Y.
Результат действия оператора A
на
элемент x
обозначают
Y
= A
x
или Y
= A
(x).
Если элементы X
и Y
связаны соотношением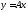 ,
тоY
называют образом
элемента X;
элемент X
- прообразом
элемента
Y.
,
тоY
называют образом
элемента X;
элемент X
- прообразом
элемента
Y.
Множество
элементов линейного пространства X,
для которых определено действие
оператора A,
называют областью
определения
оператора и обозначают
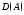 .
Множество элементов линейного
пространстваY,
которые являются образами элементов
из области определения оператора A,
называют образом
оператора и обозначают
.
Множество элементов линейного
пространстваY,
которые являются образами элементов
из области определения оператора A,
называют образом
оператора и обозначают
 .
.
Оператор A, действующий в линейном пространстве X называется линейным оператором, если
 для
для
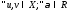 .
.
Пример:
Образ линейного пространства
 есть пространство.
есть пространство.
Док-во:
Пусть
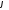 – л. о., действующий в
– л. о., действующий в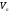 .
. сущ.
сущ.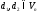 ,
такие, что
,
такие, что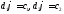 .
.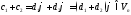 ,
, .
.
Линейный оператор и его матрица. Переход к другому базису
Рассмотрим
линейный оператор A,
действующий в конечномерном линейном
пространстве X,
![]() и
пусть
и
пусть![]() базис
вX.
Обозначим через
базис
вX.
Обозначим через
![]() образы
базисных векторов
образы
базисных векторов![]() .
.
Матрица
 столбцами
которой являются координаты образов
базисных векторов, называется матрицей
линейного оператора
в заданном базисе.
столбцами
которой являются координаты образов
базисных векторов, называется матрицей
линейного оператора
в заданном базисе.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно - каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
![]() с
одной стороны, связывают координаты
образа
с
одной стороны, связывают координаты
образа
![]() с
координатами прообразаX,
с другой стороны - описывают действие
оператора, заданного матрицей A.
с
координатами прообразаX,
с другой стороны - описывают действие
оператора, заданного матрицей A.
Единичное преобразование Е, ставящее в соответствие вектору тот же самый вектор Ех=х.
Нулевое преобразование – преобр-е ставящее в соотв. каждому вектору х нулевой вектор.
Основная теорема о линейном операторе.
Пусть
![]() - некот. базис вn-мерном
пространстве Х, А – линейное преобразование
в Х.
- некот. базис вn-мерном
пространстве Х, А – линейное преобразование
в Х.
Для любых n векторов g1,g2, …,gn существует одно и только одно линейное преобразование А, такое, что Ае1=g1, Ае2=g2,…, Аеn=gn.
Док-во:
Докажем, что А определяется векторами Ae1, Ae2,…, Aen.
Пусть x=m1e1+m2e2+…+mnen – произвольный вектор из R. Тогда Ax=A(m1e1+m2e2+…+mnen)= m1Ae1+m2Ae2+…+mnAen => Ax однозначно определяется по Ae1, Ae2,…, Aen.
Докажем, что для g1,g2, …,gn существует л.о. А, такой, что Аеi=gi. Поставим в соответствие векторам ei векторы gi, произвольному вектору x=m1e1+m2e2+…+mnen поставим в соответствие вектор m1g1+m2g2+…+mngn. Т.к. в-р х выражается через ei вполне однозначно, то ему ставится в соответствие вектор Ax. Преобразование A определенное таким образом, является линейным.
Обозначим
координаты вектора gk
в базисе e1,…,en
через а1k,a2k,…,ank,
т.е.
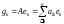 .
Совокупность чисел
.
Совокупность чисел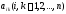 образует матрицу
образует матрицу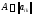 ,
которая является матрицей линейного
преобразованияA
в базисе
,
которая является матрицей линейного
преобразованияA
в базисе
![]() .
.
Т.о., мы доказали, что при заданном базисе линейному преобразованию А однозначно соотв. матрица, и обратно кажд. матр. соотв. лин. преобразование.
Связь между матрицами одного и того же линейного оператора в разных базисах
Если
в базисе
![]() линейный
оператор
линейный
оператор![]() имеет
матрицуA,
в базисе
имеет
матрицуA,
в базисе
![]() -
матрицуB,
а S
- матрица перехода от первого базиса
ко второму, то
-
матрицуB,
а S
- матрица перехода от первого базиса
ко второму, то
![]()
Произведение и сумма линейных операторов
Если
f
и g
- линейные операторы пространства
![]() с
матрицамиA
и B
в базисе
с
матрицамиA
и B
в базисе
![]() ,
то операторы произведения
,
то операторы произведения![]() и
суммы
и
суммы![]() -
линейные и имеют в том же базисе матрицыBA
и A
+ B
соответственно.
-
линейные и имеют в том же базисе матрицыBA
и A
+ B
соответственно.
Линейный
оператор
![]() называетсяобратным
линейному
оператору
называетсяобратным
линейному
оператору
![]() ,
если
,
если![]() Обозначение:
Обозначение:![]()
Для
существования
![]() необходимо
и достаточно, чтобыf
был невырожденным оператором. Если A
- матрица оператора f
в некотором базисе, то оператор
необходимо
и достаточно, чтобыf
был невырожденным оператором. Если A
- матрица оператора f
в некотором базисе, то оператор
![]() в
том же базисе имеет матрицу
в
том же базисе имеет матрицу![]() .
.
Образ и ядро линейного оператора
Рассмотрим
линейный оператор А,
действующий в конечномерном линейном
пространстве Х.
Доказано, что образ
![]() линейного
оператора - линейное пространство.
линейного
оператора - линейное пространство.
Размерность
образа линейного оператора называется
рангом
оператора,
обозначается
![]() .
.
Ядром
линейного оператора
называется множество элементов из Х,
образом которых является нулевой
элемент. Ядро оператора обозначают
![]() :
:![]() .
Ядро линейного оператора - линейное
пространство; размерность ядра линейного
оператора называетсядефектом
оператора,
обозначается
.
Ядро линейного оператора - линейное
пространство; размерность ядра линейного
оператора называетсядефектом
оператора,
обозначается
![]() :
:![]() .
.
Для
линейного оператора, действующего в
n-мерном линейном пространстве
![]() ,
справедливы следующие утверждения:
,
справедливы следующие утверждения:
сумма ранга и дефекта оператора равна размерности пространства, в котором действует оператор:
 ;
;ранг оператора равен рангу его матрицы;
ядро оператора совпадает с множеством решений линейной однородной системы с матрицей А, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
Собственные значения и собственные векторы линейного оператора
Пусть А - линейный оператор, действующий в линейном пространстве.
Число λ называется собственным значением, а ненулевой вектор х - соответствующим собственным вектором линейного оператора А, если они связаны между собой соотношением Ах=λ х
Пусть А - матрица оператора в некотором базисе.
Собственные
значения оператора и соответствующие
им собственные векторы связаны
соотношением
![]() ,
где Е- единичная матрица, а 0 - нулевой
элемент пространства Х. Это означает,
что собственный вектор оператора
является ненулевым решением линейной
однородной системы
,
где Е- единичная матрица, а 0 - нулевой
элемент пространства Х. Это означает,
что собственный вектор оператора
является ненулевым решением линейной
однородной системы![]() ,
которое существует тогда и только
тогда, когда
,
которое существует тогда и только
тогда, когда![]() .
Следовательно, собственные значения
линейного оператора могут быть вычислены
как корни уравнения
.
Следовательно, собственные значения
линейного оператора могут быть вычислены
как корни уравнения![]() ,
а собственные векторы - как решения
соответствующих однородных систем.
,
а собственные векторы - как решения
соответствующих однородных систем.
Уравнение
![]() называетсяхарактеристическим
уравнением
оператора, а многочлен
называетсяхарактеристическим
уравнением
оператора, а многочлен
![]() характеристическим
многочленом
оператора.
характеристическим
многочленом
оператора.
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
хар. многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно λ;
линейный оператор, действующий в n-мерном линейном пространстве имеет не более n различных собственных значений;
собственные векторы, отвечающие различным собственным значениям, линейно независимы;
если линейный оператор, действующий в n-мерном линейном пространстве X, имеет n различных собственных значений, то собственные векторы оператора образуют базис в пространстве X ; этот базис называют собственным базисом оператора;
матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.
Инвариантные подпространства
Пусть А – линейное преобразование в R. Линейное подпространство R1 называется инвариантным относительно A, если для каждого вектора х из R1 вектор Ах также принадлежит R1.
Тривиальные инв. подпространства – состоящее лишь из нуля и все пространство.
Пример
1. Пусть R – трехмерное пространство и А – поворот вокруг некоторой оси, проходящей через нуль. Инвар подпростр-ва – ось вращения(одномерное); плоскость, проход. через начало координат и ортогональная к оси.
2. Пусть R – произвольное n-мерное пространство и А – произвольное линейное преобразование в нем. Тогда образ М и ядро N преобразования А явл. инвариантными подпространствами. Пусть у є М => Ау є М по определению. Аналогично и с ядром преобразования.
Каноническая форма матрицы линейного оператора
λ-матрица над пространством P – выражение вида
 ,
где
,
где
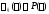
А-λE – пример λ-матриц. Числовая матрица - λ-матрица 0й степени.
λ-матрица имеет канонический вид, если
1)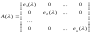 -
диагональная.
-
диагональная.
2)
старший коэффициент при
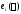 равен 1.
равен 1.
3)

Если на главной диагонали 0, то они расположены в нижней части, ненулевые элементы в верхней части главной диагонали.
Всякую λ-матрицу можно привести к каноническому виду конечным числом элементарных преобразований.
Построим цепь преобразований.
1.
Если A(λ)=||0||
теорема доказана. => пусть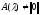
2.
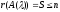 т.е. ранг матрицы меньшеn
, в каноническом виде на главной диагонали
будет S
ступеней и n-S
нулей
т.е. ранг матрицы меньшеn
, в каноническом виде на главной диагонали
будет S
ступеней и n-S
нулей

Индукция по n
1)
n=1
A(λ)=(ae(x))
– достаточно умножить A(λ)
на
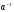 (существует,
т.к. а не равно 0).
(существует,
т.к. а не равно 0).
2)
 -
-
3) n
Пусть
в A(λ)
существует не равный 0 элемент
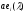 .
Поместим его в левый верхний угол и
умножим первую строку на
.
Поместим его в левый верхний угол и
умножим первую строку на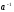 (существует,
т.к. а не равно 0). Получим:
(существует,
т.к. а не равно 0). Получим:
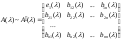
Нужно
доказать, что
 и
и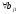 кратны
кратны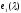 .
.
Пусть
 ,
, ,
но
,
но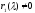 => умножая 1 столбец на (-q)
и прибавляя его к j-тому,
а затем транспонируя, получим, что
=> умножая 1 столбец на (-q)
и прибавляя его к j-тому,
а затем транспонируя, получим, что
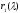 - в левом верхнем углу, на месте
- в левом верхнем углу, на месте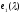 ,
чего быть не может, т.к. никакими эл.
преобразованиями нельзя поставить на
место
,
чего быть не может, т.к. никакими эл.
преобразованиями нельзя поставить на
место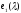 многочлен меньшей степени. =>
многочлен меньшей степени. => =>
=>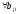 кратны
кратны .
.
Умножая,
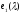 на (-q)
и складывая с 1ым , получаем нули в
первой строке, аналогично с 1ым столбцом.
на (-q)
и складывая с 1ым , получаем нули в
первой строке, аналогично с 1ым столбцом.
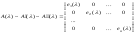 Для
матрицы порядка n-1
теорема доказана.
Для
матрицы порядка n-1
теорема доказана.
Докажем,
что
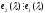
Пусто
 ,
, ,
но
,
но .
Аналогично,
.
Аналогично, .
Теорема доказана.
.
Теорема доказана.
Def.
Жордановой
(верхней) клеткой
размера mxm
(или порядка m),
соответствующей собственному значению
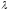 называется квадратная матрица вида
называется квадратная матрица вида
 .
.
Def.
Жордановой
матрицей
называется матрица, состоящая из
диагональных блоков
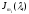 и
нулей вне этих блоков:
и
нулей вне этих блоков:

Теорема (Жордана) о приведении матрицы оператора к жордановой форме. Для любого линейного оператора комплексного линейного пространства существует базис (жорданов базис) , в котором его матрица имеет жорданову нормальную форму.
Теорема
Жордана.(Эквивалентная
формулировка) Каждая квадратная матрица
А порядка n
над алгебраически замкнутом поле (в
частности над комплексном поле С)
приводится к жордановой нормальной
форме. Именно, существует невырожденная
матрица S,
для которой
 -
матрица, состоящая из диагональных
блоков , представляющих собой жордановы
клетки.
-
матрица, состоящая из диагональных
блоков , представляющих собой жордановы
клетки.
Доказательство.
Жорданов
базис пространства V
- объединение базисов инвариантных
относительно оператора f
подпространств,
дающих в качестве прямой суммы само
пространство V.
Матрица оператора в таком базисе
клеточно-диагональная. Диагональные
клетки этой матрицы – матрицы сужений
оператора f
на соответствующих подпространствах.
Вид матриц ограничений оператора f
на циклических
подпространствах определяется базисом
выбранном в каждом из этих
циклических
подпространств. Если циклическое
подпространство принадлежит корневому
подпространству с собственным значением
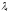 и натянуто на векторы жордановой цепочки
и натянуто на векторы жордановой цепочки ,
то
,
то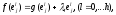 и по формулам (***) имеем:
и по формулам (***) имеем: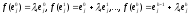 .
.
Столбцы
матрицы оператора – это координатные
столбцы образов базисных векторов,
поэтому матрица сужения оператора f
в рассматриваемом
базисе будет иметь вид: -
жордановой клетки порядка (h+1)#
-
жордановой клетки порядка (h+1)#
Лин. операторы в евклидовом пространстве и унитарном пространстве
Действительное
линейное пространство E
называется евклидовым,
если каждой паре векторов
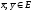 сопоставляется число
сопоставляется число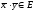 так, что
так, что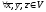 и
и выполняются аксиомы:
выполняются аксиомы:
I.
![]()
II.
![]()
III.
![]()
IV.
![]()
