Существование устойчивого стационарного состояния

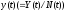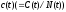Сейчас мы покажем, что экономика в конечном итоге достигнет состояния устойчивости/равновесия – ситуация, в которой производство на одного работника , потребление на одного работника и основной капитал на одного работника 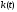не изменяются с течением времени.

Теорема 4.1.1 (Существование единственной устойчивости и равновесия)

Если и 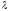удовлетворяют

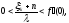(4.1.11)

то существует единственное положительное значение 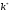для уравнения (4.1.10) такое, что . Точка равновесия, 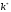, асимптотически стабильна в области .

Доказательство: введем функцию

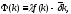
где 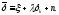Для любых 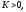по непрерывности мы имеем

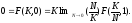
В итоге мы имеем

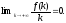
Это гарантирует, что для любого 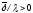существует 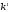такое, что 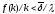для любых 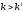. С другой стороны

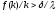Следовательно, существует такое, что для 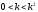, что означает 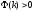для 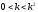. так как 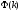непрерывно, теорема о промежуточном значении гарантирует, что существует хотя бы одна точка 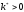такая, что 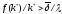, то есть

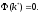
Пусть будет более чем одно положительное решение и пусть 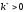обозначает одну из них, имеющую минимально значение. Для начала, запишем

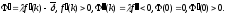
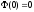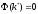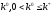Так как и , существует такое, что 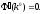Очень просто убедиться, что

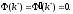
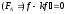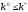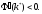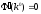Отсюда следует , что невозможно. Следовательно, мы имеем и Потому как и , мы имеем 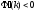для любых 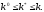Так как 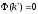и 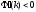для любых , мы заключаем, что невозможно найти такие 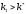, при которых 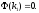Это значит, что система имеет единственное равновесие.

Сейчас мы подтвердим, что равновесие устойчиво. Точка равновесия системы асимптотически стабильна, если для любой допустимой начальной точки 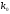решение для удовлетворяет

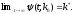
Асимптотическая стабильность может быть доказана, применяя теорему Ляпунова. Определим функцию Ляпунова

,

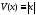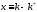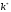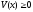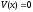где и - равновесное значение. Мы имеем и при 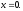Так как

Таким образом, равновесие 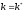глобально асимптотически стабильно.

Экономическое развитие может быть описано следующим образом. В долгосрочном периоде экономика всегда сходится в одну точку плавно к единственному равновесному соотношению труда и капитала от любой положительной отправной точки. Кроме того, вдоль траектории сбалансированного роста капитал растет с той же скоростью, с которой происходит рост населения плюс норма амортизации капитала. Важность данной модели заключается в том, что она восполняет очень простую последовательную систему, чтобы одновременно определить все значимые переменные – затраты труда и капитала к производству, продукцию производства, сбережения, потребление, инвестиции – в экономическом развитии. Вне зависимости от ее упрощенных предположений о производственной функции, сбережения и инвестиционное поведение, роль денежных переменных и так далее – это мощный инструмент, так как это дает нам логическую схему, чтобы проанализировать некоторые аспекты экономического развития.

Когда экономика достигает стационарной капиталоемкости, капитал на душу населения будет таким же, как и с течением времени, но запас капитала 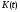остается растущим бесконечно в том же темпе, что рабочая сила . Устойчивые темпы роста модели экзогенно задаются . Это может быть подтверждено с помощью

Теперь мы формально опишем свойства динамической системы.

Мы рассмотрели динамические свойства ОМР. Она имеет долгосрочное устойчивое состояние, при котором темпы роста потребления на душу населения равны нулю. Сейчас мы рассмотрим «переходную динамику» - процесс, зависящий от времени того процесса, когда доходы на душу населения сходятся к их долгосрочному устойчивому состоянию. Разделив уравнение (4.1.10) на , мы получаем темпы роста капитала на душу населения

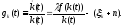
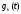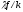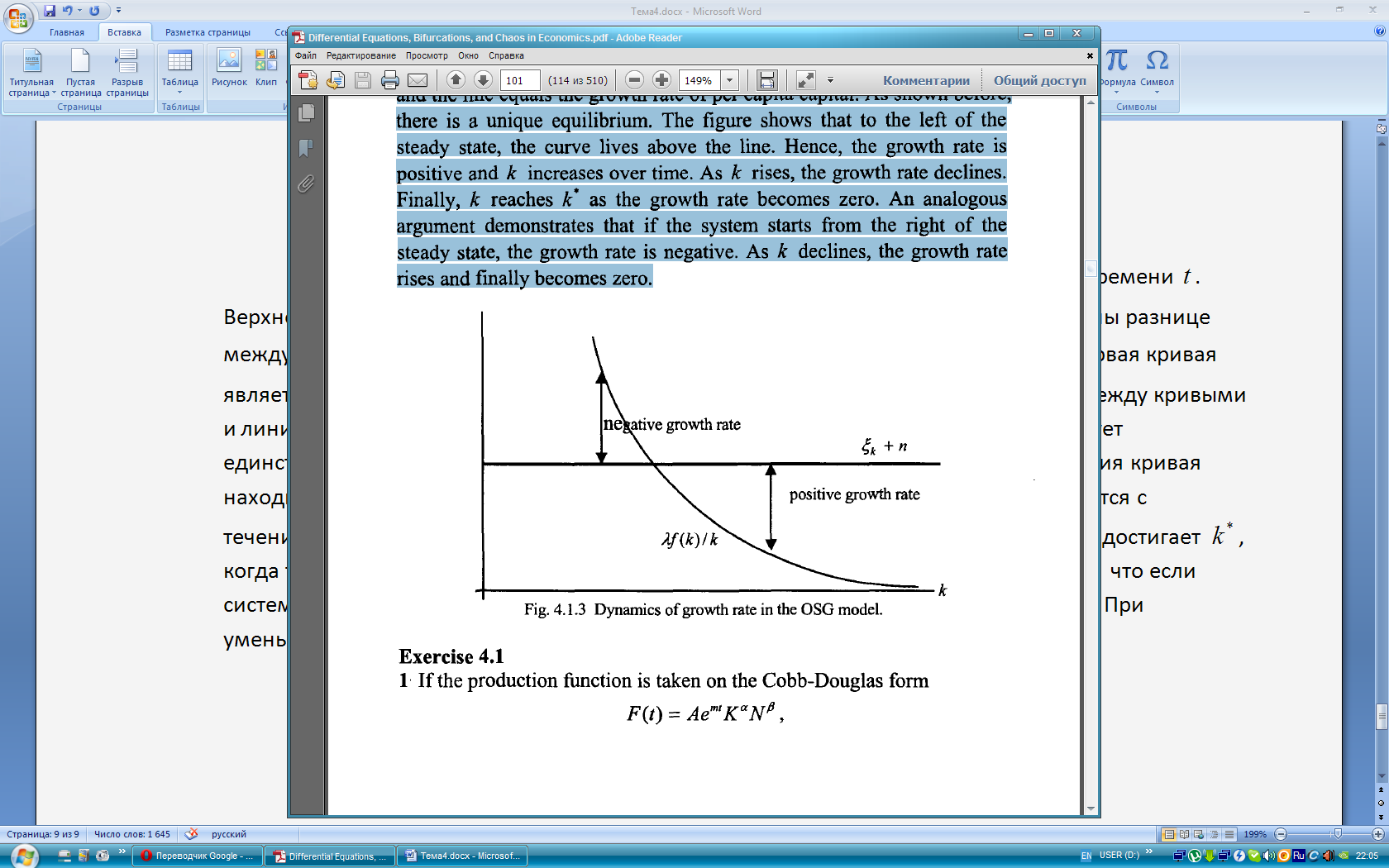
Здесь обозначает темпы роста капитала на душу населения в момент времени . Верхнее уравнение говорит о том, что темпы роста капитала на душу населения равны разнице между двумя терминами, и , которые мы нанесли на рисунок 4.1.3. Первая кривая является нисходящей, вторая – горизонтальной линией. Вертикальное расстояние между кривыми и линия равных темпов роста на душу населения. Как было показано выше, существует единственное равновесие. На рисунке показано, что слева от стационарного состояния кривая находится выше линии. Таким образом, темпы роста положительны и 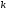увеличивается с течением времени. 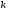Так как увеличивается, скорость роста снижается. Наконец, 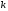достигает 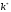, когда темпы роста становятся равными нулю. Аналогичное рассуждение показывает, что если система начинается справа от стационарного состояния, уровень роста отрицателен. При уменьшении темпы роста увеличиваются и, наконец, достигают нуля.