Раздел первый

МЕТОДЫ ПОСТРОЕНИЯ

ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ

ГЛАВА 1

МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

1.1. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

1.1.1. ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ. УРАВНЕНИЕ ЭЙЛЕРА

Вариационное исчисление представляет собой раздел математики, занимающийся поиском функций, на которых некоторые величины, от них зависящие, достигают макси­мума или минимума. При построении оптимальных систем управления вариационные методы носят вспомогательный характер, так как с их помощью успешно решаются лишь частичные задачи оптимизации.

Рассмотрим ряд общих положений классического вариационного исчисления пока вне их связи с проблемами управления. Пусть дан некоторый класс функций . Если каждой функции этого класса можно поставить в соответствие число , то говорят, что является функционалом и обозначается . Таким образом, функционал представляет переменную величину, которая при каждой функции из некоторого класса принимает определенное численное значение. Функционал является своеобразной функцией от функции, т. е. функцией, у которой аргументом является функция. Например, определенный интеграл при каждой квадратично интегрируемой функции принимает конкретное численное значение и, следовательно, является функционалом этой функции.

Простейшая задача, изучаемая в вариационном исчислении, заключается в следующем. Задан функционал

(1.1)

с известными пределами интегрирования . Здесь — известная функция указанных аргументов, однозначна и непрерывна вместе со своими частными производными до второго порядка включительно. Пусть функция относится к классу однозначных и непрерывных в промежутке функций, имеющих в этом промежутке непрерывные первые производные. Такие функции принято называть гладкими. Обозначим этот класс функций символом . Следовательно, . Если заданы значения функции в граничных точках , т. е. известны , то функции , проходящие через заданные точки , называют допустимыми. Тогда задача заключается в том, что среди допустимых функций необходимо найти такую, на которой функционал (1.1) достигает наименьшего значения, т. е. выполняется условие

(1.2)

Для определенности будем говорить о минимизации функционала, так как от задачи максимизации некоторого функционала всегда можно перейти к задаче минимизации функционала - .

При поиске решения задачи будем сравнивать различные допустимые функции, в определенном смысле близкие друг другу. Условимся две функции на отрезке называть близкими в смысле близости нулевого порядка, если расстояние между функциями, определенное как

т. е. как максимальное значение модуля разности функций, мало. Две функции называют близкими в смысле близости первого порядка, если малы расстояния и между функциями, и между их производными, т. е. малы величины

При решении задачи (1.2) .сравнивают допустимые функции, близкие в смысле близости первого порядка, так как функционал (1.1) зависит и от , и от . Если значение функционала на некоторой кривой меньше, чем на всех других допустимых кривых, близких в смысле близости нулевого порядка, то на этой кривой достигается сильный минимум. Если аналогичная ситуация обнаруживается среди кривых, близких в смысле близости первого порядка, то достигается слабый минимум. Сильный минимум является одновременно и слабым (но не наоборот), так как ищется среди широкого класса близких в смысле близости нулевого порядка функций. В изучаемой задаче ищем слабый минимум.

Для решения задачи необходимо найти условия, которым должна удовлетворять функция с тем, чтобы при переходе к любой другой близкой в смысле близости первого порядка функции значение функционала увеличилось. Предположим, что решение задачи найдено, тогда соответствующую функцию обозначим символом и перейдем от этой функции к другой , где —некоторое малое число; —произвольная гладкая функция из класса , удовлетворяющая ограничениям . Функция в силу введенных ограничений является допустимой. Функция называется вариацией функции . Подставим в (1.1) и рассмотрим функционал как функцию параметра :

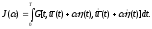
Разложим эту функцию в ряд Маклорена по степеням :

Производные в этом разложении вычисляются в точке . Второе и третье слагаемые называются первой и второй вариациями функционала соответственно.

Покажем, что необходимым условием экстремума функционала является равенство

(1.3)

Приращение функционала , обусловленное переходом от функции к функции , будет

Здесь учтено, что в соответствии с определением функции выполняется равенство 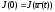. Предположим, что условие (1.3) не выполняется; но если на функции функционал достигает наименьшего значения, то должно выполняться неравенство . При малых это эквивалентно условию

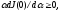(1.4)

потому что слагаемые ряда Маклорена, содержащие и т. д., при будут меньше линейного члена. Неравенство (1.4) должно выполняться при любых по знаку. Однако это возможно лишь при вырождении неравенства в равенство . Так как , то из последнего соотношения следует условие (1.3), известное под названием «равенство нулю первой вариации функционала» и являющееся необходимым условием экстремума функционала.

Развернем выражение (1.3). В соответствии с определением функции 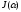имеем

Проинтегрируем второе слагаемое по частям. Для этого обозначим 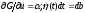, тогда

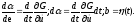
С учетом свойств функции находим

что позволяет записать

Условие (1.3) приобретает вид

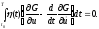(1.5)

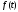Теперь воспользуемся леммой Лагранжа: если для каждой непрерывной функции имеем , где функция непрерывна при , то при всех . Применив эту лемму к (1.5), приходим к уравнению

(1.6)

Получили уравнение Эйлера, имеющее первостепенное значение в вариационном исчислении и представляющее собой искомое необходимое условие минимума функционала .

Если учесть, что производная является функцией трех переменных — и, следовательно,

то уравнение Эйлера можно переписать в развернутой форме

(1.7)

Отсюда видно, что уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка. Его решение зависит от двух постоянных интегрирования, т. е. , которые находятся из условия прохождения функции через заданные граничные точки .

Если среди допустимых функций существует функция, доставляющая минимум функционалу , то она будет решением уравнения Эйлера, т. е. экстремалью. Но на любых экстремалях функционал не обязан достигать экстремальных значений, так как (1.6) является необходимым, но не достаточным условием. Эта ситуация подобна той, которая возникает при исследовании на экстремум некоторой функции: точки, в которых производная функции обращается в нуль, могут не соответствовать экстремуму функции, а являться, например, точками перегиба. Если уравнение Эйлера не удовлетворяется ни при какой функции , то в классе гладких дифференцируемых функций экстремум функционала не существует.

1.1.2. Условия лежандра

При решении вариационных задач необходимо ответить на вопрос, максимум или минимум достигается на некоторой экстремали. Для ответа на этот вопрос используют условия Лежандра.

Рассмотрим снова приращение функционала . Так как первая вариация функционала на экстремали обращается в нуль, знак приращения функционала при малых будет определяться его второй вариацией. Следовательно, функция обеспечивает минимум, если 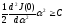. Рассмотрим детальнее функцию

Используя правила дифференцирования функции сложного аргумента, находим

что позволяет записать

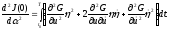
Обозначив , т. е. положив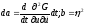проинтегрируем среднее слагаемое по частям:

Следовательно, с учетом свойств функции в точках 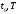получим

(1.8)

Из (1.8) следует: для выполнения условия 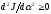необходимо, чтобы . Покажем это. Пусть , тогда, пользуясь произвольностью функции , ее можно подобрать так, что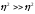. Для этого достаточно выбрать малую по абсолютному значению, но быстро и резко изменяющуюся функцию . В результате второе слагаемое в (1.8) будет превалировать над первым, подынтегральная функция окажется отрицательной и вторая вариация также окажется отрицательной, что противоречит исходному утверждению. Отсюда вытекают следующие необходимые условия Лежандра: для достижения на некоторой экстремали минимума функционала необходимо, чтобы во всех точках этой экстремали выполнялось условие

(1.9)

для достижения максимума необходимо

(1.10)

В точках, где , возможны изломы экстремали. Действительно, разрешим уравнение (1.7) относительно :

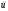Во всех точках, где , по этой формуле можно вычислить значение второй производной. Следовательно, экстремаль в этом случае является гладкой функцией. В тех точках, где , вторая производная обращается в бесконечность и, следовательно, сама экстремаль имеет излом, т. е. является кусочно-гладкой функцией. Наконец, если производная тождественно равна нулю, что возможно в случаях, когда функция не зависит от или зависит линейно, т. е. имеет структуру

то вторая производная для экстремали не существует. Функционалы в подобных ситуациях называют вырожденными. Последние обладают особыми свойствами: достигают минимума, если [29]

достигают максимума при противоположном знаке неравенства.

Пример 1.1. Исследовать на экстремум функционал

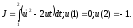
В данном случае и уравнение Эйлера имеет вид . Дважды интегрируя по , определяем . Постоянные интегрирования находят из граничных условий , т. е. . Следовательно, экстремум достигается на кривой . Условия Лежандра показывают , т. е. на данной кривой функционал достигает минимального значения.

Пример 1.2. Исследовать па экстремум функционал

Имеем , т. е. не зависит от , и уравнение Эйлера оказывается алгебраическим относительно с решением . Эта экстремаль не проходит через заданные граничные точки, и, следовательно, вариационная задача решения не имеет. Если бы граничные условия были, заданы в форме , то экстремаль проходила бы через эти точки и кривая была бы решением задачи.

Пример 1.3. Исследовать на экстремум функционал

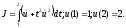
Уравнение Эйлера можно переписать как , где — константа. Из этого уравнения находим 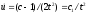, после интегрирования 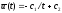. В соответствии с граничными условиями. , т.е. , и окончательно . Условия Лежандра , и на экстремали достигается минимум.

Уравнение Эйлера и условия Лежандра являются необходимыми для экстремума. В математических курсах по вариационному исчислению устанавливаются и достаточные условия. Приведем одно из них. Для того чтобы функция доставляла слабый минимум или максимум функционалу (1.1), достаточно соблюдение следующего: а) функция удовлетворяет уравнению Эйлера (1.6), т. е. является экстремалью; б) на экстремали выполняется усиленное условие Лежандра для минимума или для максимума; в) уравнение

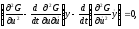
называемое уравнением Якоби, имеет решение 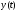, удовлетворяющее условию и не обращающееся в нуль ни в одной точке при .

В общем случае уравнение Якоби является линейным однородным с переменными параметрами. В выражения производных надо подставить экстремаль , т. е. коэффициенты уравнения являются известными функциями .

Например, в случае задачи, рассмотренной в примере 1.1, имеем ; тогда уравнение Якоби выглядит так: 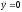. Его решение , где — некоторые постоянные. Из условия следует и . Легко видеть, что в случае решение при всех . Следовательно, выполняются пп. «а» — «в» достаточного условия и на найденной в примере 1.1 кривой действительно достигается минимум.