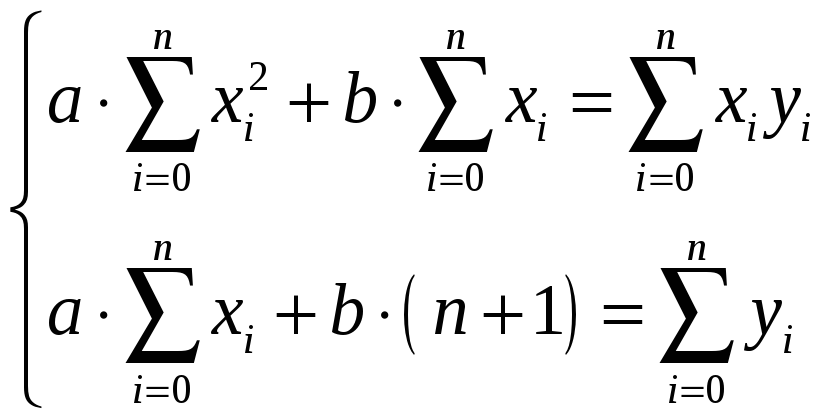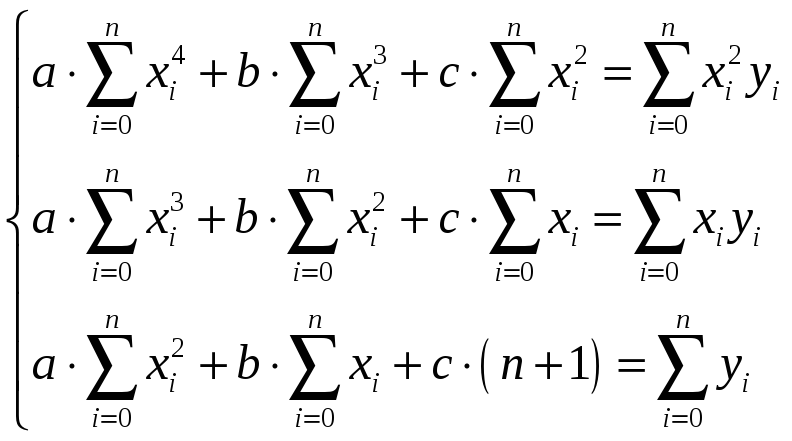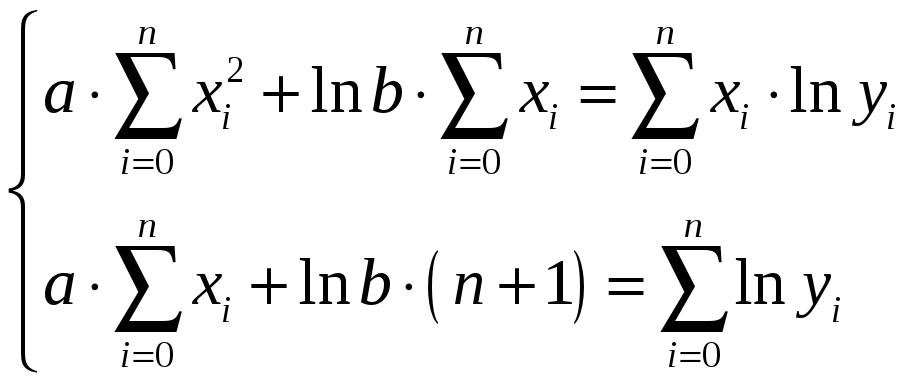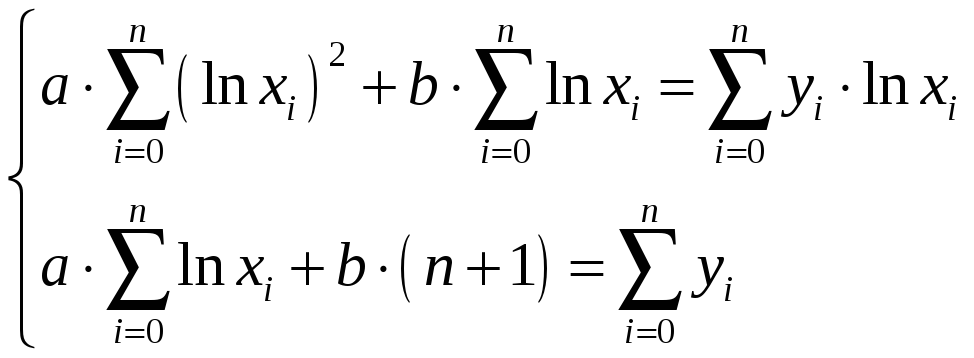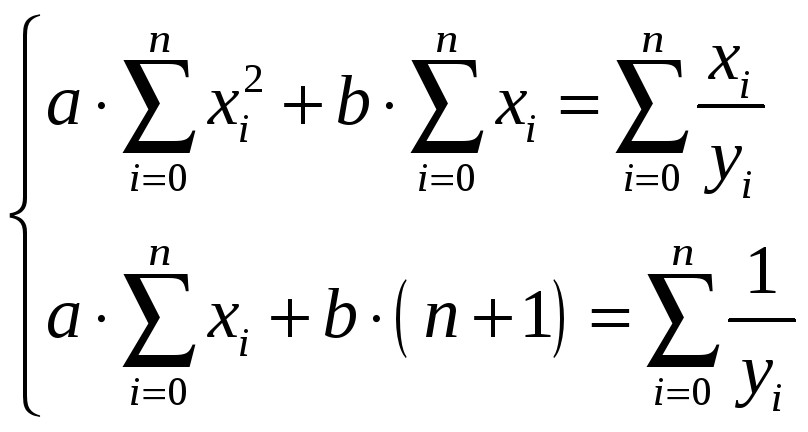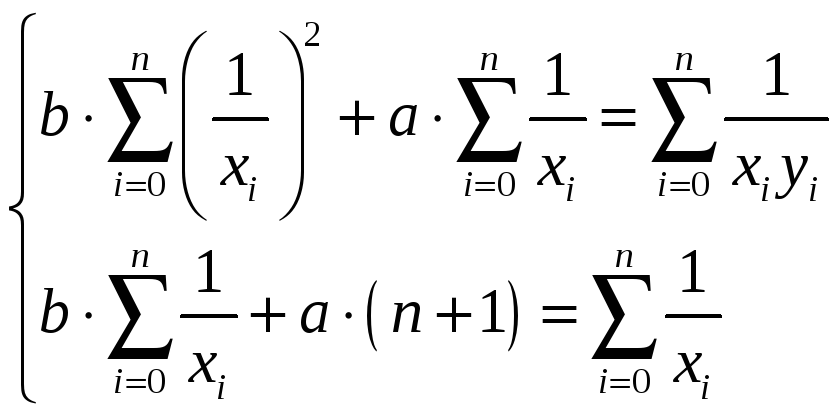Обработка данных эксперимента. Построение эмпирической зависимости
Пусть в результате эксперимента получена таблица значений некоторой функции:
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Требуется построить
аналитическую зависимость
![]() такую, которая бы в точках таблицы
такую, которая бы в точках таблицы
![]() принимала значения по возможности как
можно более близкие к
принимала значения по возможности как
можно более близкие к
![]() (в задаче интерполяции должно выполняться
точное равенство
(в задаче интерполяции должно выполняться
точное равенство
![]() ).
).
Для решения задачи
будем предполагать, что
![]() – это точная зависимость, и она неизвестна.
Мы будем искать
– это точная зависимость, и она неизвестна.
Мы будем искать
![]() .
.
Построение функции
![]() происходит в два этапа:
происходит в два этапа:
-
Выяснение общего вида зависимости: в системе координат отмечаются точки
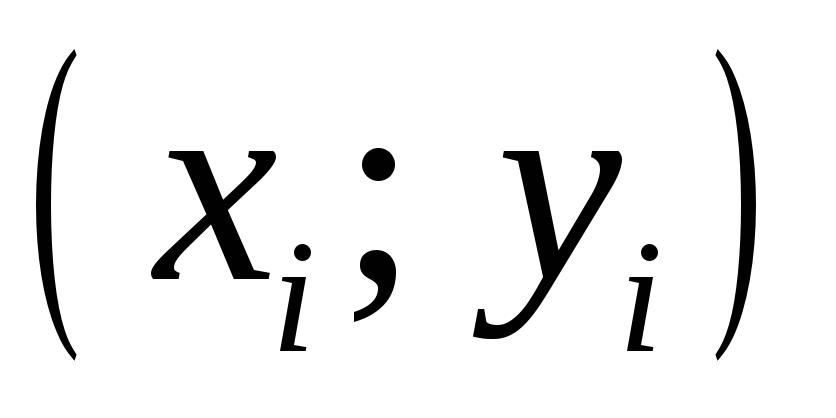 ,
«сквозь» них проводится плавная линия
и по ее форме определяется зависимость
из известного класса функции:
,
«сквозь» них проводится плавная линия
и по ее форме определяется зависимость
из известного класса функции:-
Линейная
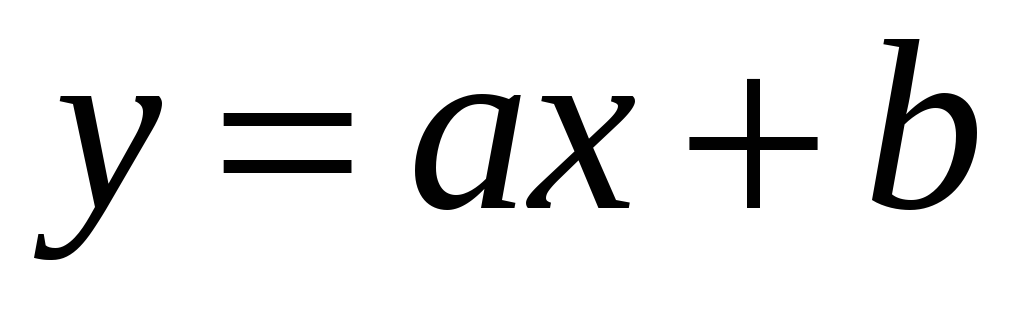
-
Квадратичная
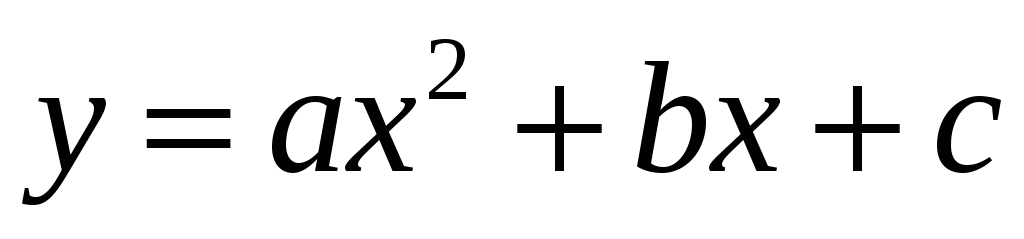
-
Степенная

-
Показательная
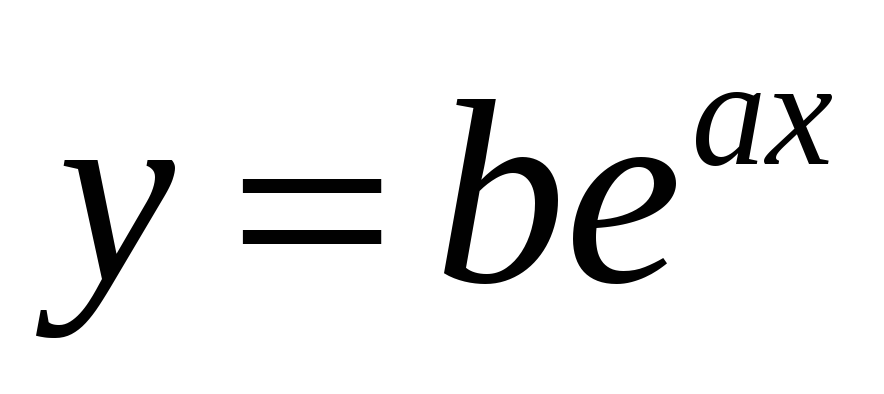
-
Обратная пропорциональность

-
Логарифмическая
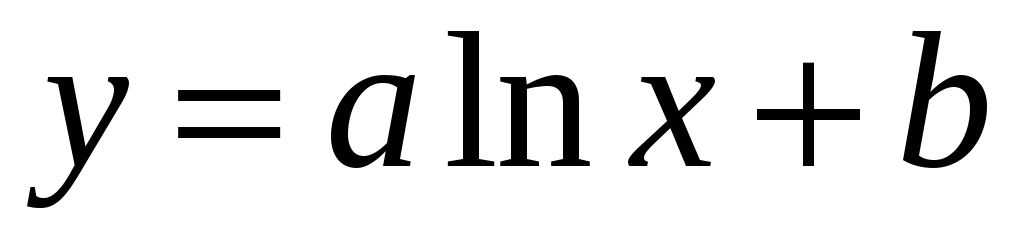
-
Дробно-рациональная
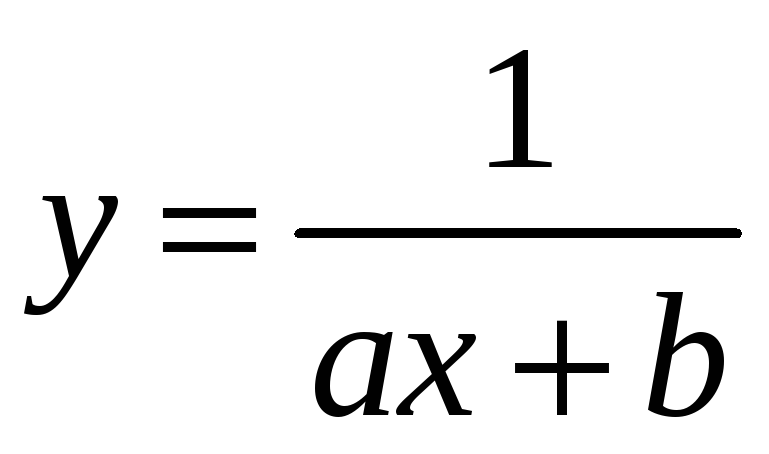 ,
,

-
-
Уточнение зависимости (определение параметров
 )
по методу наименьших квадратов (МНК):
составляется нормальная система
уравнений для выбранной зависимости,
из которой и находятся неизвестные
параметры (см. ниже таблицу)
)
по методу наименьших квадратов (МНК):
составляется нормальная система
уравнений для выбранной зависимости,
из которой и находятся неизвестные
параметры (см. ниже таблицу)
Поскольку для
одной и той же таблично заданной
экспериментальной функции можно выбрать
несколько аналитических зависимостей,
то возникает вопрос о качестве описания
аналитической функцией данных
эксперимента. Для этого вводятся величины
![]() – отклонения измеренного значения
– отклонения измеренного значения
![]() от вычисленного по выбранной
экспериментальной зависимости, и
составляется сумма их квадратов
от вычисленного по выбранной
экспериментальной зависимости, и
составляется сумма их квадратов
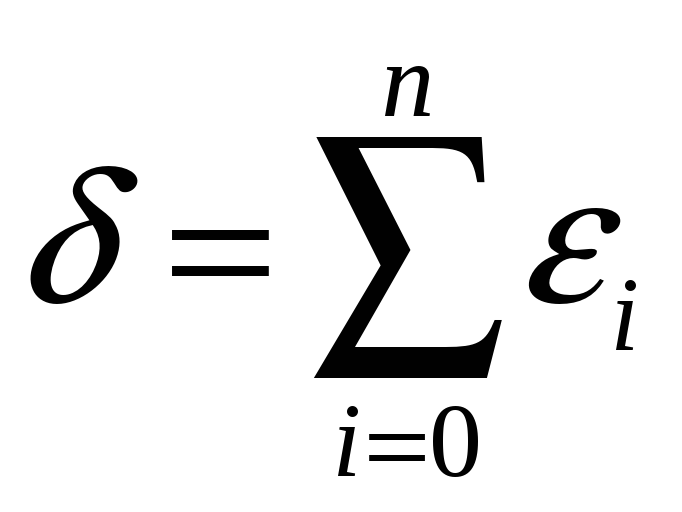 .
Из двух приближающих функций лучшей
следует считать ту, для которой сумма
квадратов отклонений меньше.
.
Из двух приближающих функций лучшей
следует считать ту, для которой сумма
квадратов отклонений меньше.
Нормальные системы для определения параметров экспериментальной зависимости
|
Линейная
|
|
|
Квадратичная
|
|
|
Степенная
|
|
|
Показательная
|
|
|
Обратная
пропорциональность
|
|
|
Логарифмическая
|
|
|
Дробно-рациональная
|
|
|
Дробно-рациональная
|
|
Пример:
|
|
4 |
6 |
8 |
10 |
12 |
14 |
|
|
1,5 |
1,9 |
2 |
2,2 |
2,2 |
2,3 |
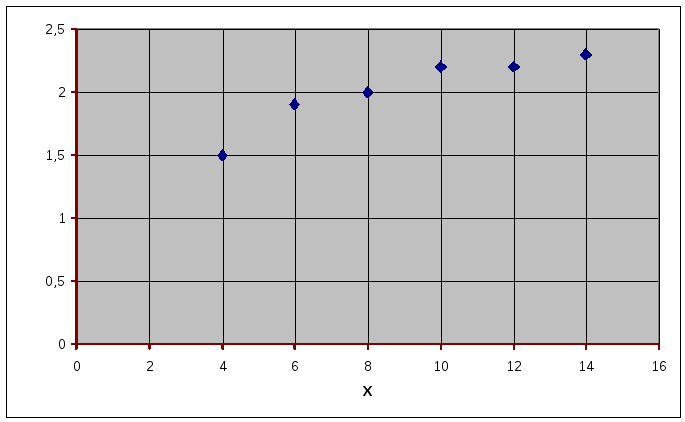
Изобразим точки в одной системе координат и оценим вид предполагаемой зависимости. Точки располагаются вблизи некоторой прямой, а также вблизи графика некоторой логарифмической функции. Поэтому построим две зависимости – линейную и логарифмическую и оценим точность их приближения.
Определим параметры
линейной зависимости
![]() .
Все необходимые расчеты оформим в виде
таблицы (первые 4 столбца):
.
Все необходимые расчеты оформим в виде
таблицы (первые 4 столбца):
|
|
|
|
|
|
|
|
|
|
0 |
4 |
1,5 |
6 |
16 |
1,1785 |
0,3215 |
0,103362 |
|
1 |
6 |
1,9 |
11,4 |
36 |
1,4749 |
0,4251 |
0,180710 |
|
2 |
8 |
2 |
16 |
64 |
1,7713 |
0,2287 |
0,052304 |
|
3 |
10 |
2,2 |
22 |
100 |
2,0677 |
0,1323 |
0,017503 |
|
4 |
12 |
2,2 |
26,4 |
144 |
2,3641 |
-0,1641 |
0,026929 |
|
5 |
14 |
2,3 |
32,2 |
196 |
2,6605 |
-0,3605 |
0,129960 |
|
сумма |
54 |
12,1 |
114 |
556 |
|
|
0,510768 |
Составляем нормальную систему:
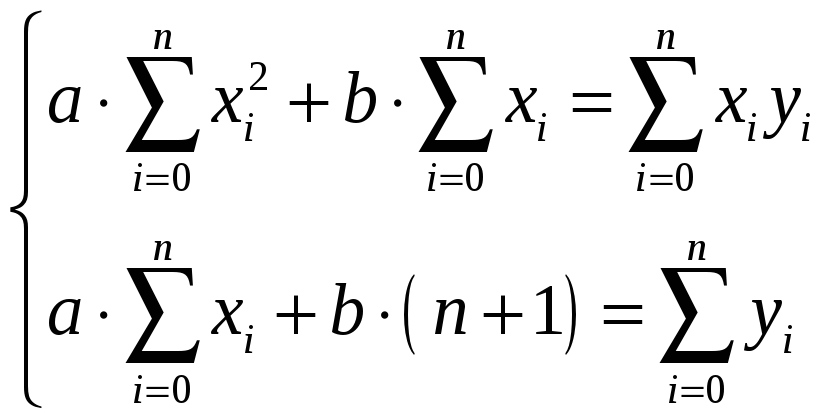
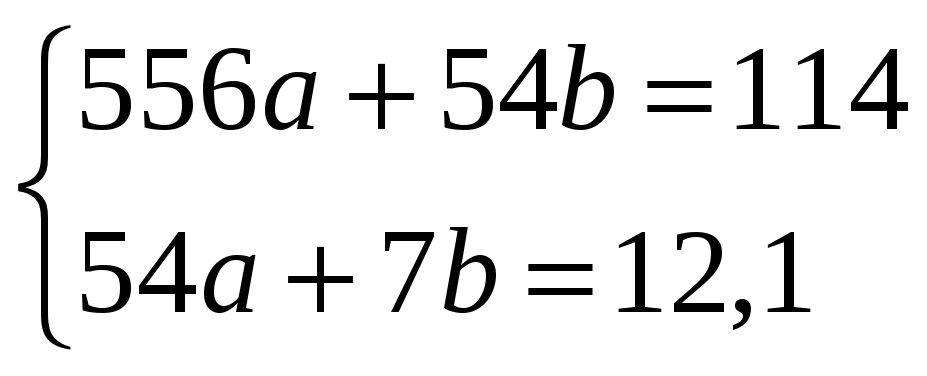 .
.
Решением нормальной
системы является пара
![]() ,
,
![]() .
Таким образом, приближающая линейная
зависимость имеет вид:
.
Таким образом, приближающая линейная
зависимость имеет вид:
![]() .
Для оценки качества приближения вычислим
отклонения и сумму их квадратов (см.
последние 3 столбца таблицы):
.
Для оценки качества приближения вычислим
отклонения и сумму их квадратов (см.
последние 3 столбца таблицы):
![]() .
.
Определим параметры
логарифмической зависимости
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
1,5 |
1,386294 |
1,921812 |
2,079442 |
1,569664 |
-0,069664 |
0,004853 |
|
1 |
6 |
1,9 |
1,791759 |
3,210402 |
3,404343 |
1,818724 |
0,081276 |
0,006606 |
|
2 |
8 |
2 |
2,079442 |
4,324077 |
4,158883 |
1,995434 |
0,004566 |
0,000021 |
|
3 |
10 |
2,2 |
2,302585 |
5,301898 |
5,065687 |
2,132502 |
0,067498 |
0,004556 |
|
4 |
12 |
2,2 |
2,484907 |
6,174761 |
5,466795 |
2,244494 |
-0,044494 |
0,001980 |
|
5 |
14 |
2,3 |
2,639057 |
6,964624 |
6,069832 |
2,339182 |
-0,039182 |
0,001535 |
|
сумма |
54 |
12,1 |
12,684044 |
27,897574 |
26,244981 |
|
|
0,019551 |
Составляем нормальную систему и решаем ее:
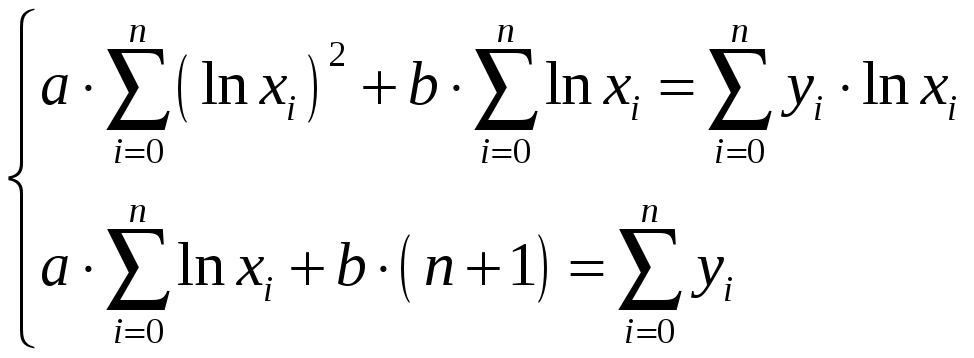
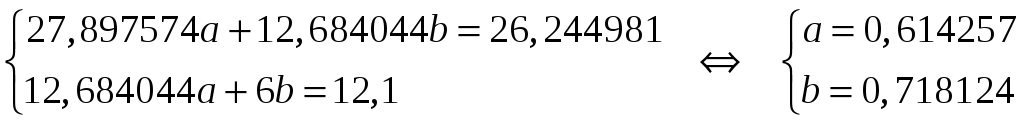
Приближающая
логарифмическая функция имеет вид
![]() .
Сумма квадратов отклонений для нее
равна
.
Сумма квадратов отклонений для нее
равна
![]() .
.
Сравнивая суммы квадратов отклонений для линейной и логарифмической приближающих функций, можно сделать вывод о том, что логарифмическая зависимость точнее описывает данные эксперимента. О большей точности логарифмической зависимости можно судить и по графику – график логарифмической зависимости проходит «ближе» к точкам-результатам эксперимента.