
- •1. Рациональные уравнения и методы их решения
- •Методы их решения
- •1. Использование области определения уравнения.
- •2. Разложение на множители.
- •3. Замена переменной.
- •Функциональные методы
- •4. Использование ограниченности функций.
- •5. Использование монотонности функций.
- •2. Рациональные неравенства и методы их решения
- •Алгебраические неравенства.
- •3. Модуль числа. Решение уравнений, содержащих переменную под знаком модуля
- •Основные свойства модуля:
- •I тип уравнений
- •II тип уравнений
- •III тип уравнений
- •IV тип уравнений
- •V тип уравнений
- •VI тип уравнений
- •4. Модуль числа. Решение неравенств, содержащих переменную под знаком модуля
- •1 Способ. Использование геометрического смысла модуля.
- •2 Способ. Использование свойства модулей: модули противоположных чисел равны.
- •3 Способ: Использование определение модуля числа.
- •4 Способ: Решение неравенства на интервалах
- •5.Уравнения. Равносильные уравнения. Уравнения–следствия. Теоремы о равносильных преобразованиях уравнений
- •Преобразования, приводящие к равносильному уравнению
- •Теоремы о равносильных преобразованиях уравнений
- •6. Неравенства. Равносильные неравенства. Неравенства-следствия. Теоремы о равносильных преобразованиях неравенств
- •7. Системы и совокупности уравнений. Основные методы решения систем уравнений
- •Системы и совокупности уравнений
- •8. Системы и совокупности неравенств
- •Основные методы решения систем двух неравенств с двумя неизвестными
- •9. Иррациональные уравнения. Основные методы решения иррациональных уравнений
- •10. Иррациональные неравенства. Основные методы решения иррациональных неравенств
- •11. Показательные уравнения. Основные методы решения показательных уравнений
- •12. Показательные неравенства. Основные методы решения показательных неравенств.
- •13. Логарифмические уравнения. Основные методы решения логарифмических уравнений
- •14 . Логарифмические неравенства. Основные методы решения логарифмических неравенств
- •15. Основные методы решения тригонометрических уравнений
- •16. Основные методы решения тригонометрических неравенств
- •17 . Уравнение с параметрами. Решение линейных уравнений с параметрами.
- •18. Уравнения с параметрами. Решение квадратных уравнений с параметрами
- •19. Методы решения уравнения . Методы решения неравенства
- •20. Обобщающий метод интервалов для решения неравенств
- •21. Основные тригонометрические функции, их свойства, графики
- •22. Обратные тригонометрические функции, графики, свойства
- •1. Метрические соотношения в окружности. Свойства хорд. Свойства секущих и касательных к окружности. Измерение углов, связанных с окружностью
- •Свойства хорд
- •2. Окружность, вписанная в треугольник. Формулы, связывающие элементы треугольника с радиусом вписанной окружности
- •3. Окружность, описанная около треугольника. Формулы, связывающие элементы треугольника с радиусом описанной окружности
- •4. Прямая Эйлера
- •5. Окружность Эйлера
- •6. Вневписанная окружность.
- •7. Центроид треугольника
- •8. Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника
- •9. Вписанные четырехугольники. Вписанные многоугольники
- •10. Описанные четырехугольники. Описанные многоугольники
- •11. Теорема Пифагора. Обобщенная теорема Пифагора.
- •12. Теорема Пифагора для четырехугольников.
- •13. Теорема Птолемея.
- •14. Методы геометрических преобразований. Симметрия. Поворот. Параллельный перенос. Подобие. Гомотетия.
- •15. Метод площадей.
- •1.Свойства параллельного проектирования. Изображение плоских фигур. Требования к проекционным чертежам.
- •2. Свойства параллельного проектирования. Изображение многоугольников и тел вращения. Теорема Польке-Шварца.
- •3.Методы построения сечений многогранников.
- •4.Взаимное расположение прямых в пространстве. Скрещивающиеся прямые. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми. Расстояние между скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
- •Взаимное расположение плоскостей в пространстве. Угол между плоскостями. Двугранный угол. Измерение двугранных углов.
- •Взаимное расположение плоскостей в пространстве. Многогранный угол. Трехгранный угол. Их свойства.
8. Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника
Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).
Свойства
Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.
Радиусы окружностей проходящих через любые три точки ортоцентрической системы равны.
Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
Точки, симметричные ортоцентру относительно его сторон, лежат на описанной окружности.
Точки, симметричные ортоцентру относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
Если О — центр
описанной окружности ΔABC, то
![]() .
.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Ортотреуго́льник (ортоцентрический треугольник) треугольника ∆ABC — треугольник, вершины которого являются основаниями высот ∆ABC.
Свойства
-
. Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
-
Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
-
Если точки A1, B1 и C1 на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что
![]() ,
,
![]() и
и
![]() ,
,
то A1B1C1 — ортотреугольник треугольника ABC.
-
Точки касания вписанной в данный треугольник окружности соединены отрезками, и в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника.
-
Ортотреугольник отсекает треугольники, подобные данному.
-
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
-
Высоты треугольника являются биссектрисами ортотреугольника.
-
Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
-
Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.
9. Вписанные четырехугольники. Вписанные многоугольники
-
Четырёхугольник, все вершины которого лежат на окружности, называется вписанным.
-
Сумма противоположных углов вписанного четырёхугольника равна 180°.
-
Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (теорема Птолемея).
-
Площадь S вписанного четырёхугольника со сторонами a, b, c, d можно вычислить по формулам:
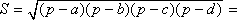
-
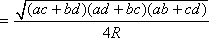 ,где
p –
полупериметр, R
– радиус окружности.
,где
p –
полупериметр, R
– радиус окружности. -
Если a, b, c, d – длины сторон четырёхугольника,
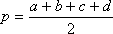 –
его полупериметр, а α
– сумма его противоположных углов, то
площадь S
четырёхугольника равна
–
его полупериметр, а α
– сумма его противоположных углов, то
площадь S
четырёхугольника равна
![]() .
.
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид:
![]() ;это
равенство и называется формулой
Брахмагупты.
Если четырёхугольник имеет и описанную
и вписанную окружности, то формула
становится совсем короткой:
;это
равенство и называется формулой
Брахмагупты.
Если четырёхугольник имеет и описанную
и вписанную окружности, то формула
становится совсем короткой:
![]() .
.
Если четырехугольник вписан в окружность, то сумма его противоположных углов равна 1800 (свойство вписанных четырехугольников).
1
Действительно, пусть четырехугольник
АВСД
вписан в окружность (рис.3.61).Тогда сумма
его углов
А
и
С
измеряется полусуммой дуг
ВСП
и
ВЛП,
составляющих полную окружность, а потому
равна 180°. И Рассмотрим первый случай.
Продолжим тогда сторону
ВА
за точку
А
до пересечения с окружностью
Р
в точке
М
и проведем хорду
МБ
(рис.3.63).Четырехугольник
ВСБМ
вписан в окружность
Р.
Как доказано,
АС+ АМ=
180о.
Но
АА >АМ
(как внешний угол треугольника БМА),
а значит АА+АС>180о.
Получили противоречие. Следовательно,
точка
А
не может лежать внутри круга, ограниченного
окружностью
Р.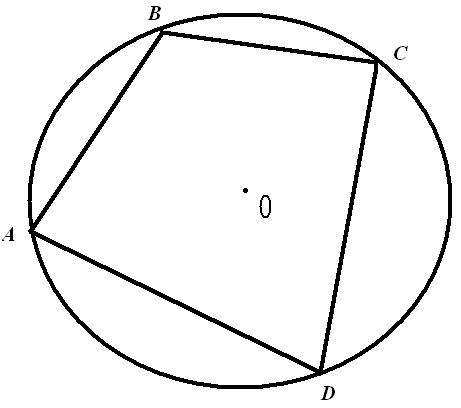
Тэарэма
(аб акружнасці, апісанай каля правільнага
многавугольніка). Каля любога правільнага
многавуголь- ніка можна апісаць
акружнасць, і прытым толькі адну.
Дадзена: А 1
А 2А3
••• Аn
—правільны многавугольнік. Даказаць:
існуе пункт, роўнааддалены ад усіх
вяршынь. Ён адзіны. Доказ.
1. Дакажам існаван- не. Няхай О — пункт
перасячэння бісектрыс вуглоў
Аг
іА2
(рыс. 61). Злучым пункт О адрэзкамі з
астатнімі вяршынямі многаву- гольніка
і дакажам, што
ОА1
= ОА2
= ... =
ОАп.
1) Паколькі
А1
=А2
то
1
= =3,
значыць, трохвугольнік А1А20
раўнабедраны і ОАг
= ОА2.
2) Трохвугольнікі А1А20
і
А3А2О
роўныя па дзвюх стара- нах і вуглу паміж
імі (А1А2
= АзА2,
А2О
— агульная старана і 3
= 4),
значыць, ОА3
=
ОАг.
3)Аналагічна можна даказаць, што ОА4 = ОА2, ОА5 = ОА3 і г.д. 4) Такім чынам, ОА1 = ОА2 = ... = ОАт, значыць, пункт О роўнааддалены ад усіх вяршынь многавугольніка. Таму акружнасць со (О, ОА1) з'яўляецца апісанай каля многаву- гольніка.
2. Дакажам адзінкавасць. Для гэтага разгледзім якія-не- будзь тры вяршыні многавугольніка, напрыклад, А1 А2, А3. Паколькі праз гэтыя пункты праходзіць толькі адна акруж- насць, то і каля многавугольніка А1, А2, ... Аn можна апісаць толькі адну акружнасць.
