12. Окружность, вписанная в треугольник. Формулы, связывающие элементы треугольника с радиусом вписанной окружности
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Т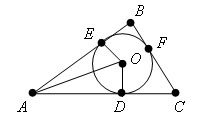
еорема.
Центр окружности, вписанной в треугольник,
является точкой пересечения его
биссектрис. Доказательство.
Пусть ABC данный, O – центр вписанной в
него окружности, D, E и F – точки касания
окружности со сторонами. Δ AEO = Δ AOD по
гипотенузе и катету (EO = OD – как радиус,
AO – общая). Из равенства треугольников
следует, что ∠
OAD = ∠
OAE. Значит AO биссектриса угла EAD. Точно
также доказывается, что точка O лежит
на двух других биссектрисах треугольника.
Удобно уметь вычислять площадь, если даны три стороны.
Так
как S
= 0,5aha;
ha
=
,
где р – полупериметр треугольника;
поэтому, S
=
.
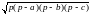Эта формула была известна еще в древнем
мире и носит название формулы
Герона.
Е
Рис. 4
сли
знать эту формулу, то любую высоту
треугольника удобно вычислять, посчитав
предварительно площадь треугольника.
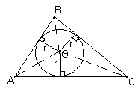
Выведем формулу, связывающую площадь треугольника с радиусом вписанной окружности (см. рис. 4).
S = SAOB + SBOC + SCOA = 0,5cr + 0,5ar + 0,5br = pr.
Также
существует формула:
,
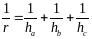где
- высоты треугольника
13. Окружность, описанная около треугольника. Формулы, связывающие элементы треугольника с радиусом описанной окружности
О
кружностью
называется фигура, состоящая из множества
точек плоскости, расположенных на
одинаковом расстоянии от некоторой
точки О этой же плоскости, называемой
центром окружности, а отрезок, соединяющий
центр с какой-либо точкой окружности,
— радиусом
окружности. Окружность называется
описанной около треугольника, если она
проходит через все его вершины.
Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
Доказательство. Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OB как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника. Ч.т.д.
Докозательство 2способ
Пусть a и b – серединные перпендикуляры к сторонам AC и BC треугольника ABC, а точка O – точка их пересечения. Из свойств серединного перпендикуляра AO = OC = OB. Следовательно, точка O лежит на серединном перпендикуляре к стороне AB. Таким образом, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Кроме того, точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Отсюда, по определению, центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника. Теорема доказана. Ч.т.д. |
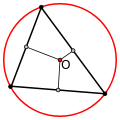
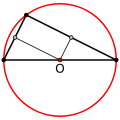
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного— вне треугольника, у прямоугольного— на середине гипотенузы.
Остроугольный |
Тупоугольный |
Прямоугольный |
3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Радиус описанной окружности может быть найден по формулам
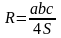
Где: a,b,c — стороны треугольника, α — угол, лежащий против стороны a, S — площадь треугольника.