
- •Раздел 7
- •1. Система координат на плоскости
- •1.1. Декартова система координат
- •Повторение некоторых сведений из раздела «Элементы векторной алгебры»
- •1.2. Преобразование системы координат
- •1. Параллельный перенос осей координат
- •2. Поворот осей координат
- •1.3. Полярная система координат
- •1.4. Линии на плоскости
- •2. Уравнение прямой на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •2.3. Каноническое уравнение прямой
- •2.4. Параметрические уравнения прямой
- •2.5. Уравнение прямой, проходящей через две точки
- •2.6. Уравнение прямой в отрезках
- •2.7. Расположение двух прямых на плоскости
- •Условия параллельности двух прямых
- •Условия перпендикулярности двух прямых
- •Угол между двумя прямыми
- •2.8. Расстояние от точки до прямой
- •3. Линии второго порядка
- •3.1. Окружность
- •3.2. Эллипс
- •3.3. Гипербола
- •3.4. Парабола
- •4. Уравнения поверхности и
- •4.1. Системы координат в пространстве
- •1. Прямоугольные декартовы координаты в пространстве
- •2. Цилиндрические координаты
- •3. Сферические координаты
- •4.2. Уравнения поверхности и линии в пространстве
- •5. Уравнение плоскости
- •5.1. Общее уравнение плоскости
- •5.6. Расположение двух плоскостей Условия параллельности и перпендикулярности двух плоскостей
- •Угол между двумя плоскостями
- •5.7. Расстояние от точки до плоскости
- •6. Уравнение прямой
- •6.1. Канонические и параметрические уравнения прямой
- •6.2. Уравнение прямой, проходящей через две точки
- •6.3. Общие уравнения прямой в пространстве
- •6.4. Взаимное расположение двух прямых в пространстве
- •6.5. Угол между двумя прямыми
- •6.6. Расстояние от точки до прямой. Расстояние между двумя скрещивающимися прямыми
- •6.7. Взаимное расположение прямой и плоскости
- •Определение точки пересечения прямой и плоскости
- •Угол между прямой и плоскостью
- •7. Поверхности второго порядка
- •7.1. Канонические уравнения и поверхности второго порядка
5.1. Общее уравнение плоскости
Положение плоскости P
в пространстве вполне определено, если
известны точка
![]() ,
принадлежащая ей, и ненулевой вектор
,
принадлежащая ей, и ненулевой вектор
![]() ,
перпендикулярный к этой плоскости.
,
перпендикулярный к этой плоскости.
Постановка задачи: Составить уравнение плоскости, проходящей через точку , и вектор , перпендикулярный к этой плоскости. Вектор называется нормальным вектором плоскости.

![]() .
(5.1)
.
(5.1)
Равенство (5.1) называется уравнением плоскости с нормальным вектором и проходящей через точку .
Раскрыв скобки в уравнении (5.1), получим
![]() ,
(5.2)
,
(5.2)
где
![]() .
.
Уравнение (5.2) называется общим уравнением плоскости с нормальным вектором .
Общее уравнение плоскости (5.2) называется
полным, если все его коэффициенты
и
![]() отличны от нуля. Если же хотя бы один из
них равен нулю, то уравнение называется
неполным. Рассмотрим возможные
случаи неполных уравнений:
отличны от нуля. Если же хотя бы один из
них равен нулю, то уравнение называется
неполным. Рассмотрим возможные
случаи неполных уравнений:
1) при
![]() уравнение
уравнение
![]() определяет плоскость, проходящую через
начала координат;
определяет плоскость, проходящую через
начала координат;
2) при
уравнение
![]() с нормальным вектором
с нормальным вектором
![]() ,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
при
![]() уравнение
уравнение
![]() с нормальным вектором
с нормальным вектором
![]() ,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
при
![]() уравнение
уравнение
![]() с нормальным вектором
с нормальным вектором
![]() ,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
,
перпендикулярным к оси
,
определяет плоскость, параллельную оси
(или содержащую ее, если
);
3) при
![]() уравнение
уравнение
![]()
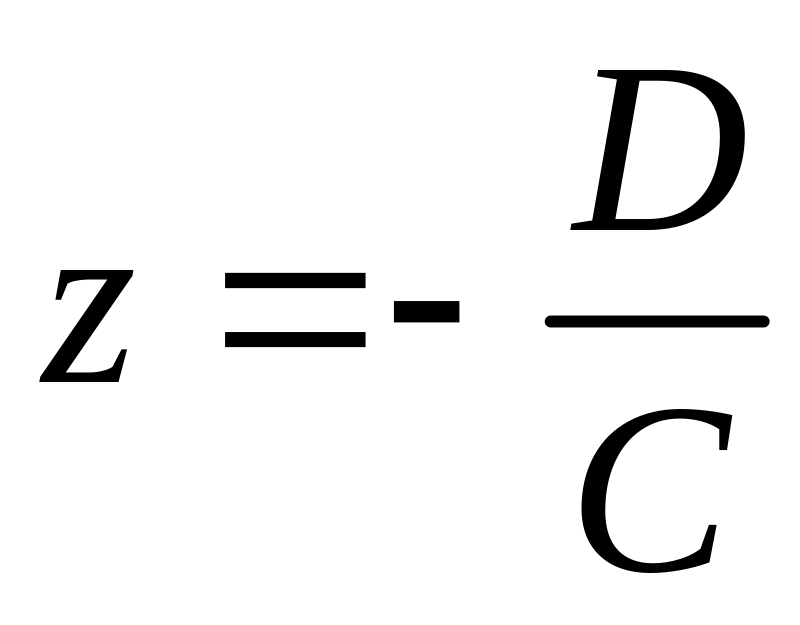 с нормальным вектором
с нормальным вектором
![]() параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
![]() .
Если
,
то уравнение
.
Если
,
то уравнение
![]() определяет плоскость
.
определяет плоскость
.
при
![]() уравнение
уравнение
![]()
![]() с нормальным вектором
с нормальным вектором
![]() параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
![]() .
Если
,
то уравнение
определяет плоскость
.
.
Если
,
то уравнение
определяет плоскость
.
при
![]() уравнение
уравнение
![]()
![]() с нормальным вектором
с нормальным вектором
![]() параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
параллельным оси
,
определяет плоскость, параллельную
плоскости
и пересекающую ось
в точке
![]() .
Если
,
то уравнение
определяет плоскость
.
.
Если
,
то уравнение
определяет плоскость
.
5.2. Уравнение плоскости,
параллельной двум данным векторам
Постановка задачи: Составить
уравнение плоскости, проходящей через
точку
,
и параллельной двум векторам
![]() и
и
![]() ,
неколлинеарных между собой.
,
неколлинеарных между собой.

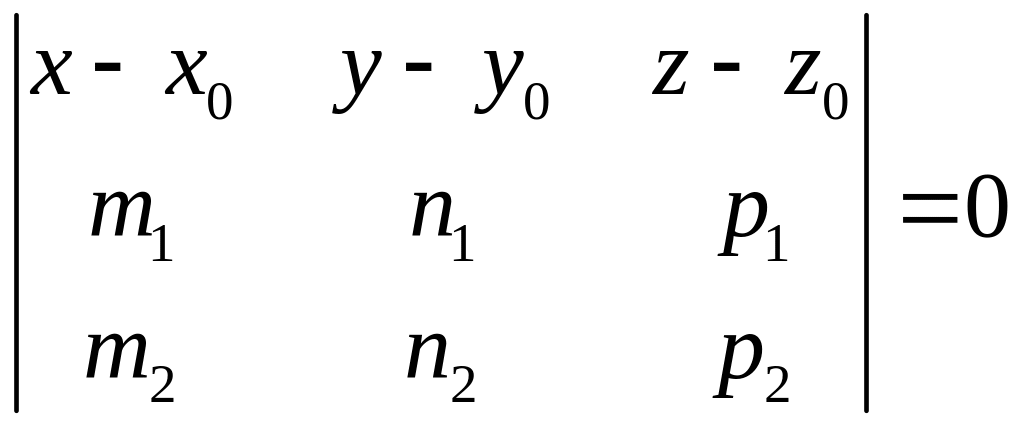 .
(5.3)
.
(5.3)
Равенство (5.3) является уравнением плоскости, параллельной векторам и и проходящей через точку .
5.3. Параметрические уравнения плоскости
Пусть плоскость P
определяется двумя неколлинеарными
векторами
и
и точкой
![]() .
.

 ,
,
или
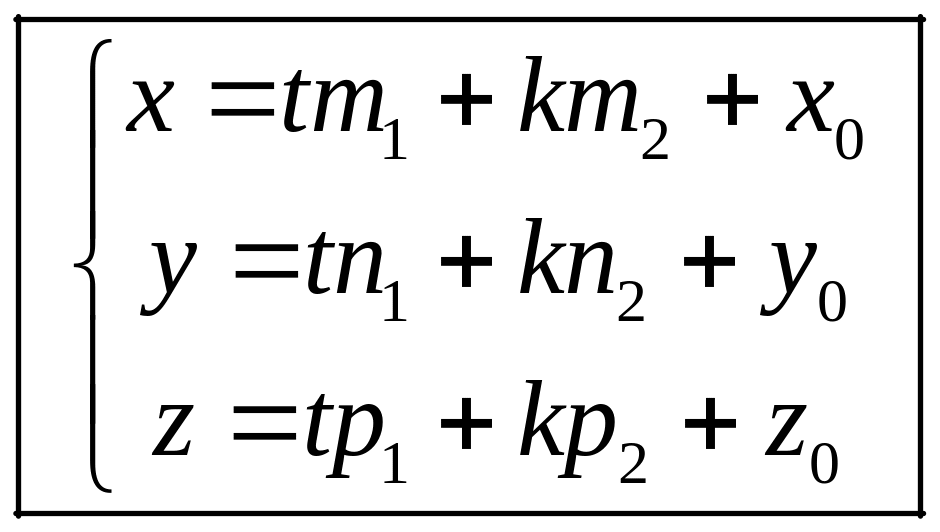 .
(5.4)
.
(5.4)
Уравнения (5.4) называются параметрическими уравнениями плоскости.
5.4. Уравнение плоскости,
проходящей через три точки
Постановка задачи: Составить
уравнение плоскости, проходящей через
три точки
![]() ,
,
![]() и
и
![]() .
.

или, используя формулу смешанного произведения в координатной форме, получаем следующее равенство
 .
(5.5)
.
(5.5)
Равенство (5.5) является уравнением плоскости, проходящей через три точки , и .
5.5. Уравнение плоскости в отрезках
Пусть плоскость на осях , и отсекает отрезки длиной , и соответственно.

Далее
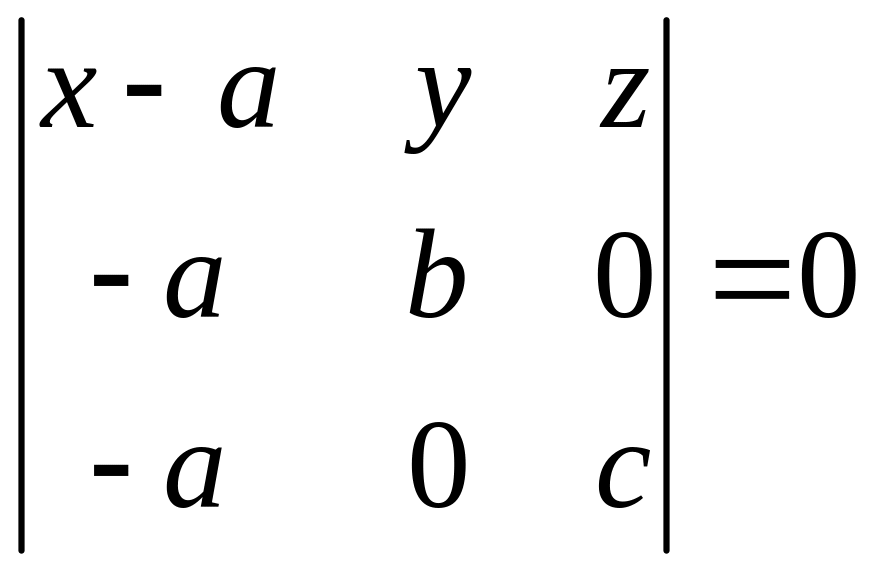 .
.
Раскрыв определитель, имеем
![]() ,
т.е.
,
т.е.
![]() или
или
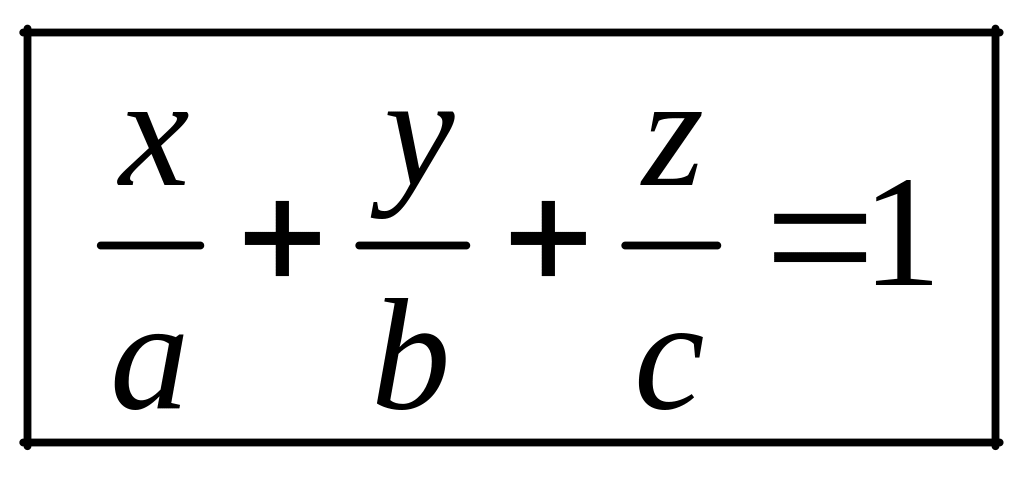 .
(5.6)
.
(5.6)
Равенство (5.6) называется уравнением плоскости в отрезках на осях. Этим уравнением удобно пользоваться при построении плоскости.
Пример 5.1. Составить уравнение
плоскости, проходящей через точку
![]() и ось
.
и ось
.
Решение. Способ 1. Так как
плоскость проходит через ось
,
то в этой плоскости лежит орт
![]() .
В этой плоскости лежит и вектор
.
В этой плоскости лежит и вектор
![]() .
.

По формуле (5.1) составляем уравнение плоскости:
![]()
![]() .
.
Способ 2. Так как плоскость
проходит через ось
,
то уравнение плоскости в общем виде
![]() .
Так как точка
принадлежит плоскости, то координаты
этой точки удовлетворяют уравнению
искомой плоскости, т.е.
.
Так как точка
принадлежит плоскости, то координаты
этой точки удовлетворяют уравнению
искомой плоскости, т.е.
![]()
![]() ,
где
,
где
![]() .
Таким образом уравнение плоскости
примет вид:
.
Таким образом уравнение плоскости
примет вид:
![]()
.
.
Способ 3. Так как плоскость
проходит через ось
,
то на этой плоскости кроме точки
можно взять точки
![]() и
и
![]() ,
принадлежащие оси
.
,
принадлежащие оси
.
По формуле (5.5) составляем уравнение плоскости:

.
.
Способ 4. Так как плоскость проходит через ось , то эта плоскость параллельна векторам и .
По формуле (5.3) составляем уравнение плоскости:

.
.
Пример 5.2. Какие отрезки отсекает на осях координат плоскость
![]() .
.
Решение. Приведем данное уравнение к уравнению в отрезках:
![]()
![]()
![]() .
.
Отсюда получаем, что на оси
плоскость отсекает отрезок
![]() ,
на оси
отрезок
,
на оси
отрезок
![]() ,
на оси
отрезок
,
на оси
отрезок
![]() .
.
