4. Двойное отношение четырех точек.

Двойным отношением четырех собственных точек A, B, C, D, лежащих на одной прямой, называется число (ABCD) = ⁼ : ⁼ .

Будем также использовать такое обозначение двойного отношения: (AB, CD). различных значений сложных отношений 4 заданных точек одной прямой может быть только шесть.

Теорема. При перестановке пар A,B и C,D значение двойного отношения сохраняется.

Свойства двойных отношений. Пусть

1. (AB, CD) = . Тогда

2. (AB, DC) = 1/ ;

3. (AC, BD) = 1 –  ;

4. (AD, BC) = 1 ^– = ;

5. (AC, DB) = ;

6. (AD, CB) = ;

Отношение разделенности (неразделенности) пар точек сохраняется при проективных преобразованиях.

5. Проективная плоскость.

Плоскость  пополненная несобственными точками всех прямых, которые лежат в плоскости  , называется расширенной или проективной плоскостью. Обозначим ее (; ¯ .

Множество всех несобственных точек расширенной плоскости называется несобственной прямой (обозначается a_ ). Остальные (обычные) прямые называются собственными.

Несобственная прямая в пространстве задается плоскостью.

Центральное проецирование расширенной плоскости на расширенную плоскость – взаимнооднозначное отображение.

Множество всех несобственных точек проективного пространства называется несобственной плоскостью (обозначается _ ). Обычные (нерасширенные) плоскости называются собственными плоскостями.

Обобщение. Проективной прямой, плоскостью, пространством называют также любое множество, которое можно взаимнооднозначно отобразить на расширенную прямую, плоскость, пространство.

6. Проективные координаты на плоскости.

Проективной системой координат (проективным репером) на проективной плоскости (; ¯ называется произвольная упорядоченная четверка точек этой плоскости R = {A₁, A₂, A_3, E}, никакие три из которых не лежат на одной прямой. Точки A₁, A₂, A₃ называются вершинами репера, а E – единичной точкой.

Выберем произвольную собственную точку O (; ¯ и будем откладывать от нее все векторы.

Вектор x;\s\up8(( порождает точку M(; ¯, если x;\s\up8(( лежит на прямой OM. Пишем ( x;\s\up8(–( ) = M.

Очевидно, что R \{0} ( x;\s\up8(( ) = (x;\s\up8(( ).

Базис B = {a1;\s\up8(( , a2;\s\up8(( , a3;\s\up8(( } в пространстве порождает репер R = {A₁, A₂, A₃, E}, если ( a1;\s\up8(( ) = A ₁ , ( a2;\s\up8(( ) = A₂ , ( a3;\s\up8(( ) = A₃, ( a1;\s\up8(( + a2;\s\up8(–( + a3;\s\up8(( ) =E . Пишем: (B ) = R .

Теорема Для любого репера R на плоскости (; ¯ существует единственный с точностью до гомотетии с центром O базис B, который порождает репер R .

Пусть базис B порождает репер R , а вектор x;\s\up8(( – точку M. Проективными координатами точки M(; ¯ в репере R называются координаты вектора x;\s\up8(–( относительно базиса B .

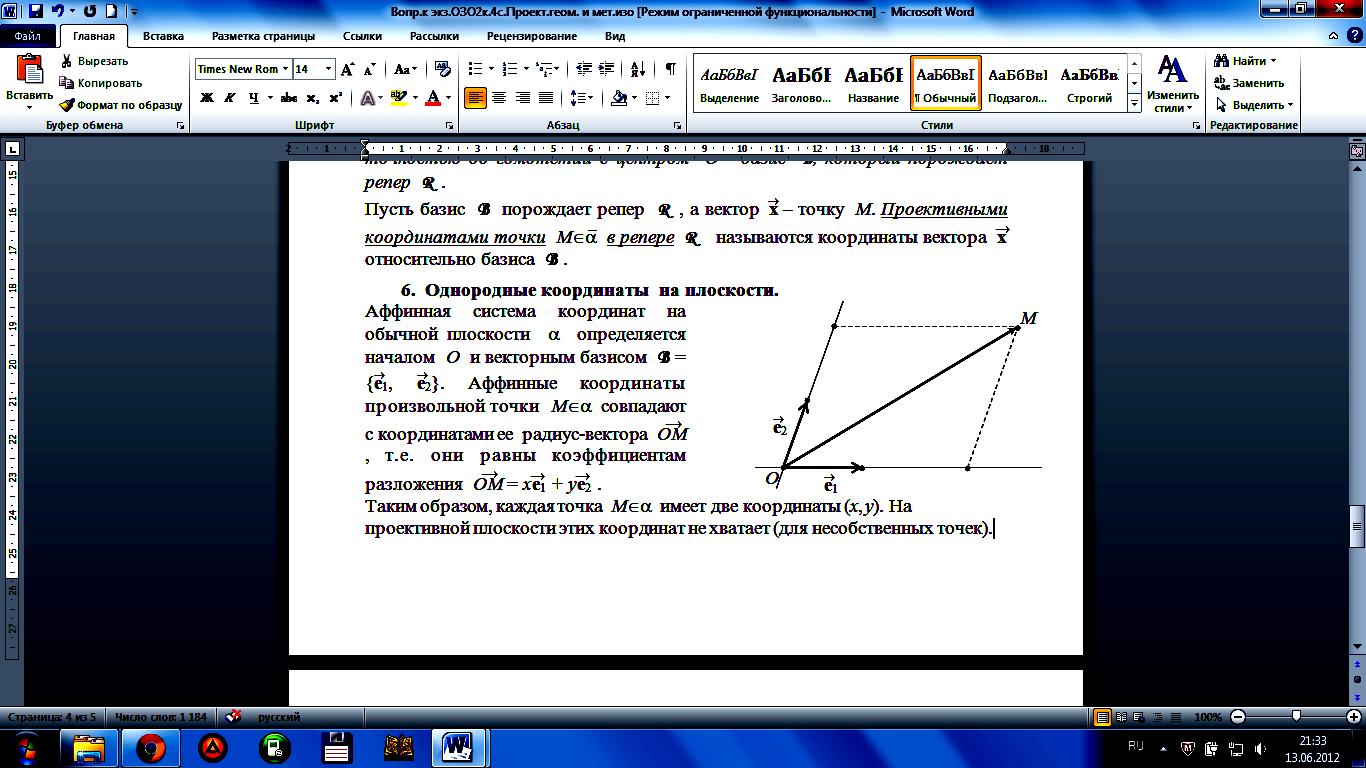
7. Однородные координаты на плоскости.

Аффинная система координат на обычной плоскости  определяется началом O и векторным базисом B = {e1;\s\up8(( , e2;\s\up8(( }. Аффинные координаты произвольной точки M совпадают с координатами ее радиус-вектора OM;\s\up10( –(, т.е. они равны коэффициентам разложения OM;\s\up10( –( = xe1;\s\up8(–( + ye2;\s\up8(–( .

Таким образом, каждая точка M имеет две координаты (x, y). На проективной плоскости этих координат не хватает (для несобственных точек). Однородными аффинными координатами собственной точки M(x, y) называются числа x₁, x₂, x₃ такие, что x = x₁/x₃ , y = x₂ / x₃ , или, что то же самое, x₁: x₂ : x₃ = x : y : 1.

Очевидно, что такие координаты определяются с точностью до пропорциональности.

Рассмотрим несобственную точку M_ . Она определяется прямой l . Пусть ее уравнение в аффинной системе координат ax + by + c = 0 . Пусть M(x, y) – произвольная собственная точка прямой. Тогда y = – (ax + с) / b, т.е. M(x, – (ax + с) / b). Значит, однородные координаты точки M будут (x, – (ax + с) / b, 1) или (b, – a – с / x, b / x). Несобственную точку прямой l; ¯можно рассматривать, как предел собственной точки, когда она бесконечно удаляется по прямой. Поэтому однородные координаты M_ получаем, как предел

lim;\s\do8(x ( ((b, – a – с / x, b / x) = (b, – a , 0)  M_(b: – a: 0).