
- •9.16. Линейные однородные дифференциальные уравнения
- •I. Основные понятия теории дифференциальных уравнений.
- •III. Линейные дифференциальные уравнения первого порядка
- •Учебный модуль №9 «Дифференциальные уравнения» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Дифференциальные уравнения»
- •9.1. Физические задачи, приводящие к дифференциальным уравнениям
- •9.2. Основные понятия теории дифференциальных уравнений
- •9.3. Дифференциальные уравнения первого порядка. Задача Коши
- •9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •9.5. Однородные дифференциальные уравнения и приводящиеся к ним
- •9.6. Линейные дифференциальные уравнения первого порядка
- •9.7. Уравнение Бернулли
- •9.8. Дифференциальные уравнения в полных дифференциалах
- •9.9. Особые решения дифференциальных уравнений первого порядка
- •9.10. Модели прикладных задач с применением дифференциальных уравнений
- •9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
- •9.12. Дифференциальные уравнения, допускающие понижение порядка
- •9.13. Понятие о краевых задачах для обыкновенных дифференциальных уравнений
- •9.14. Линейные дифференциальные уравнения высших порядков
- •9.15. Линейные однородные дифференциальные уравнения, свойства их решений. Определитель Вронского. Условия линейной зависимости и независимости решений
- •9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
- •9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
- •Вопросы к экзамену по модулю №9
- •Дифференциальные уравнения в полных дифференциалах.
9.6. Линейные дифференциальные уравнения первого порядка
Уравнение
![]() ,
,
линейное относительно
неизвестной функции и ее производной
(т.е. содержащее у
и
в первой степени), называется линейным
дифференциальным уравнением первого
порядка. Здесь p(x)
и f(x)
– непрерывные на
![]() функции, либо постоянные числа.
функции, либо постоянные числа.
Если
![]() ,
то уравнение
,
то уравнение
![]()
называется линейным
однородным
дифференциальным уравнением (левая
часть этого уравнения является однородной
функцией относительно у
и
,
так как
![]() ).
Если
).
Если
![]() ,
то уравнение называется неоднородным.
,
то уравнение называется неоднородным.
Существует несколько методов интегрирования линейных дифференциальных уравнений первого порядка. Рассмотрим некоторые из них.
Метод подстановки (Бернулли)
По этому методу искомое решение уравнения будем искать в виде
![]() ,
,
где
![]() и
и
![]() - некоторые непрерывно дифференцируемые
функции. Подставляя y
= uv
и
- некоторые непрерывно дифференцируемые
функции. Подставляя y
= uv
и
![]() в , получаем
в , получаем
![]() или
или
![]() .
.
Выберем функцию таким образом, чтобы
![]() ,
,
после чего от уравнения остается
![]() .
.
В результате получили систему двух уравнений
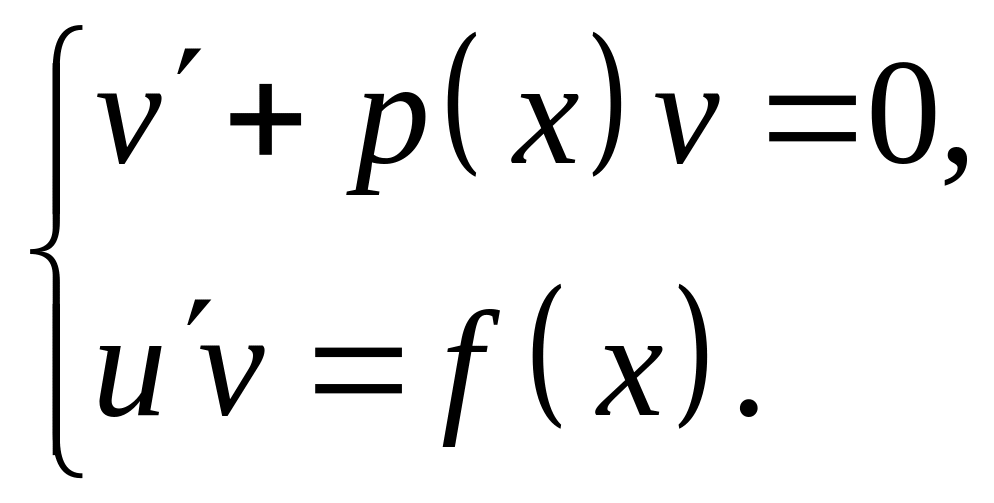
Сначала решаем
первое уравнение системы, которое
является линейным однородным
дифференциальным уравнением относительно
v
и
![]() .
Покажем, что оно, в то же время, и уравнение
с разделяющимися переменными.
.
Покажем, что оно, в то же время, и уравнение
с разделяющимися переменными.
![]()
![]()
![]() .
.
Подставляя функцию v во второе уравнение системы , получаем еще одно уравнение с разделяющимися переменными
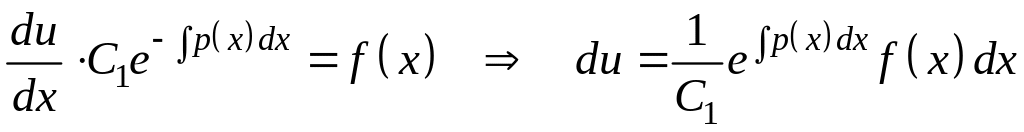 ,
откуда
,
откуда
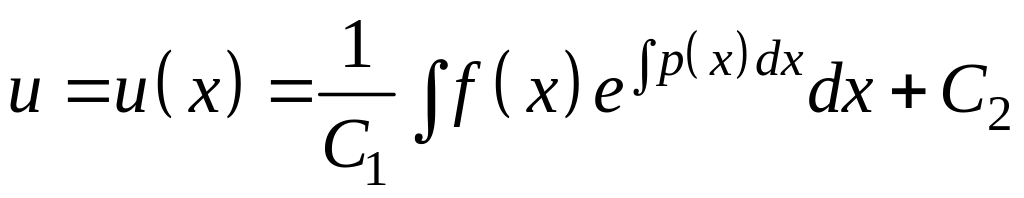 .
.
Таким образом, , т.е.

![]() .
.
Так как С1 и С2 – произвольные постоянные, то С1С2 тоже произвольная постоянная, которую можно обозначить через С. В итоге получаем, что общим решением неоднородного дифференциального уравнения будет
![]() .
.
Поскольку при
перемножении функций
![]() и
и
![]() постоянная С1
во втором слагаемом сократилась, то в
качестве функции
можно было взять
постоянная С1
во втором слагаемом сократилась, то в
качестве функции
можно было взять
![]() .
.
Пример
9.6.1. Решить
уравнение
![]() .
.
Решение. Пусть y = uv, . Тогда
![]() .
.
Составим систему
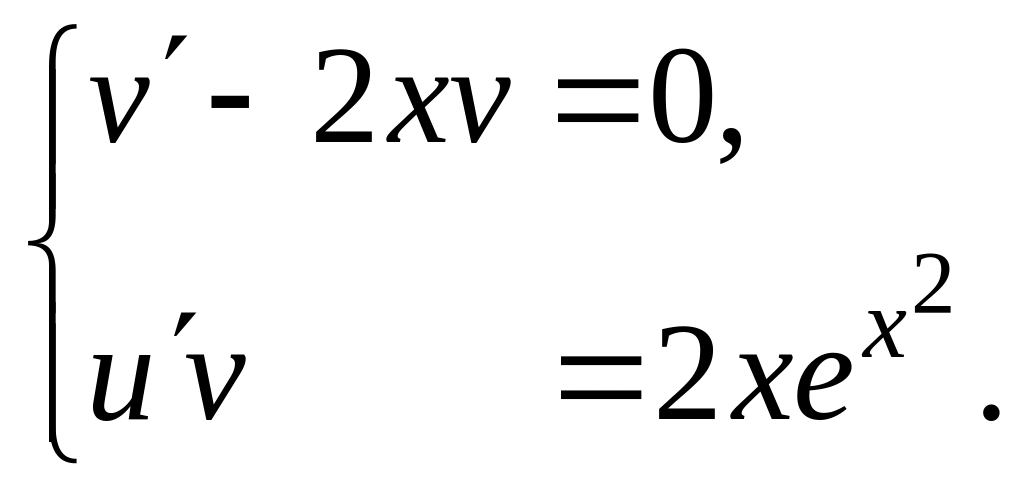
Решаем первое
уравнение
![]()
![]()
![]()
![]()
![]() (постоянную здесь не берем).
(постоянную здесь не берем).
Подставляем
во второе уравнение системы
![]()
![]()
![]()
![]() .
.
В итоге находим, что общее решение данного уравнения
, ![]() .
.
Метод вариации произвольного постоянного (метод Лагранжа)
Найдем общее решение однородного дифференциального уравнения . Разделив в нем переменные, получим
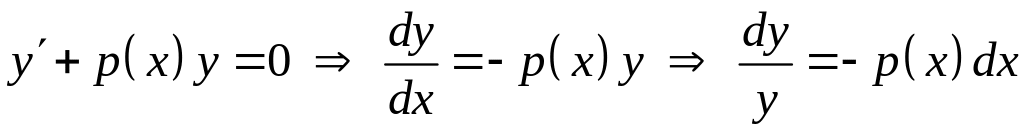
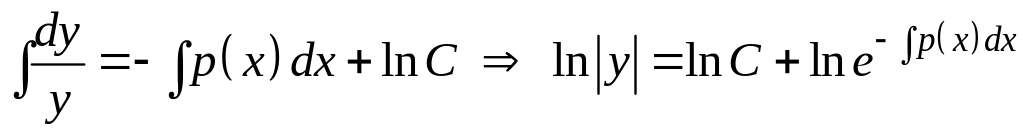
![]() ,
,
где С – произвольная постоянная.
По методу вариации (в переводе на русский язык, изменения) произвольной постоянной общее решение неоднородного уравнения ищется в виде
![]() ,
,
в котором
![]() – неизвестная дифференцируемая функция.
– неизвестная дифференцируемая функция.
Найдем
![]()
![]() .
Подставляя y
и
в , получаем
.
Подставляя y
и
в , получаем
![]() ,
,
откуда
![]()
![]() .
.
Итак, функция
![]() найдена. Подставляя ее в , находим общее
решение уравнения
найдена. Подставляя ее в , находим общее
решение уравнения
![]() ,
,
совпадающее с решением .
Пример
9.6.2. Найти
частное решение дифференциального
уравнения
![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию
![]() .
.
Решение. В
начале решаем соответствующее однородное
уравнение
![]()
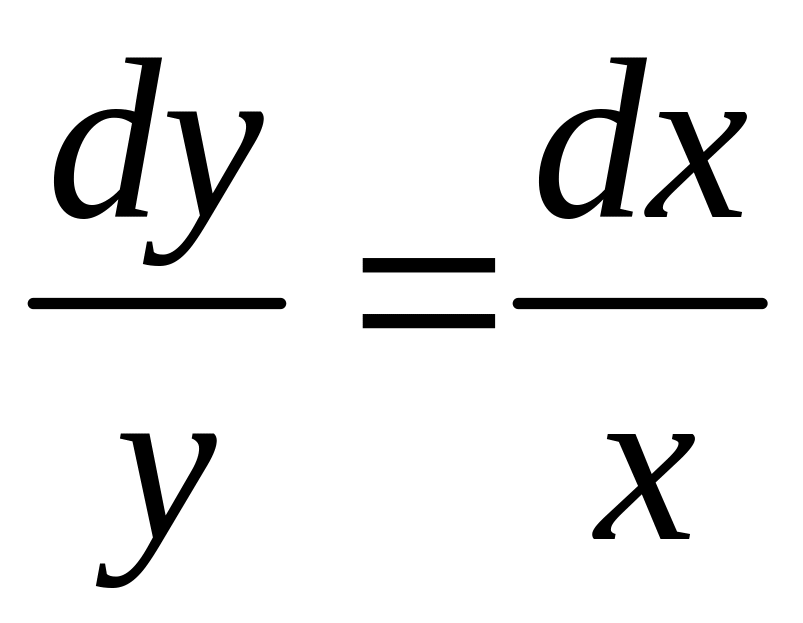
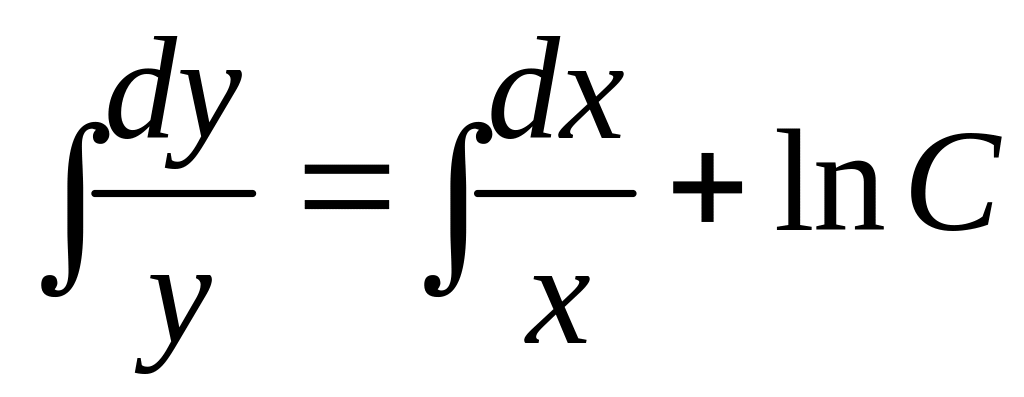
![]()
![]() .
.
В соответствии с
методом Лагранжа общее решение ищем в
виде
![]() .
Находим
.
Находим
![]() .
Тогда
.
Тогда

![]()
![]()
![]() и
и
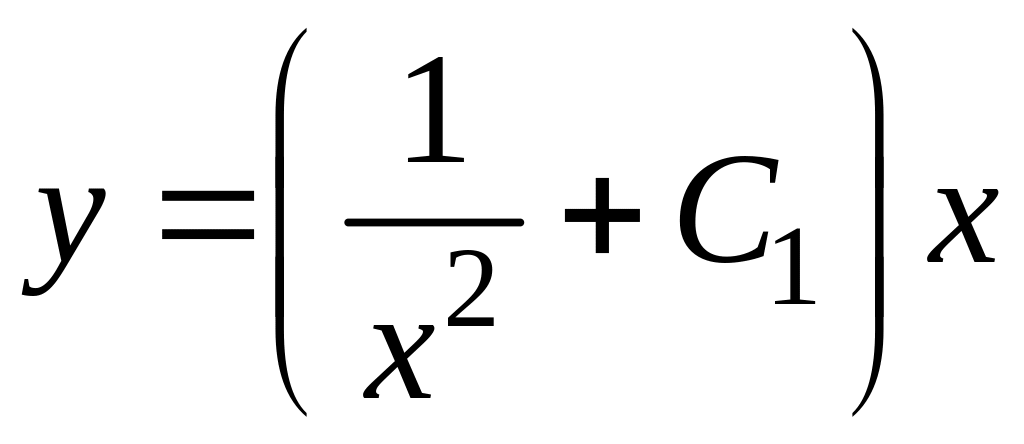 ,
или
,
или
![]() будет общим решением данного уравнения.
Из условия
имеем
будет общим решением данного уравнения.
Из условия
имеем
![]()
![]() .
.
Итак, искомым
частным решением данного уравнения,
удовлетворяющим начальному условию
,
является функция
![]() .
.
Общее решение
уравнения можно сразу найти по формуле
, подставив туда
![]() и
и
![]() и взяв три интеграла.
и взяв три интеграла.
Замечание. В приложениях часто встречаются линейные уравнения с постоянными коэффициентами
![]() ,
,
где a и b – постоянные. Его можно решить путем разделения переменных:
 .
.
