
- •Лекции на тему «Аналитическая геометрия»
- •Раздел III. Основы аналитической геометрии
- •Глава 4. Прямя и плоскость
- •4.1. Прямая на плоскости
- •4.1.1. Способы задания прямой на плоскости
- •1 Способ: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
- •2 Способ: уравнение прямой, проходящей через данную точку параллельно данному вектору.
- •3 Способ: уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом k.
- •4 Способ: уравнение прямой, проходящей через две данные точки.
- •Исследование общего уравнения прямой
- •Угол между двумя прямыми на плоскости
- •Расстояние от точки до прямой на плоскости
- •4.2. Плоскость и прямая в пространстве
- •4.2.1. Способы задания плоскости
- •1 Способ: уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •2 Способ: уравнение плоскости в координатной форме.
- •3 Способ: уравнение плоскости, проходящей через три точки.
- •4.2.2. Взаимное расположение плоскостей
- •4.2.3. Угол между двумя плоскостями
- •4.2.4. Способы задания прямой в пространстве
- •1 Способ: уравнение прямой, проходящей через данную точку параллельно данному вектору.
- •2 Способ: уравнение прямой, заданной пересечением двух плоскостей.
- •4.2.5. Взаимное расположение прямых в пространстве
- •4.2.6. Взаимное расположение прямой и плоскости
- •Фокусы, эксцентриситет, директрисы и фокальный параметр эллипса
- •1. Определение полярных координат.
- •3. Примеры уравнений линий в полярных координатах.
- •Полярные координаты в пространстве
- •Общий метод координат
- •Цилиндрические поверхности
- •Задания для самостоятельного решения
Полярные координаты в пространстве
В этой системе основными постоянными элементами являются точка 0 (полюс), ось Oz (полярная ось) и полуплоскость Ozx, примыкающая к полярной оси Oz (полярная полуплоскость).
Пусть М — какая-либо точка пространства (рис.) . Обозначим через длину радиуса-вектора ОМ, через — угол, составляемый ОМ с полярною осью Oz, и наконец, через — угол, составляемый полуплоскостью, примыкающей к оси Oz и, проходящей через точку М, с полярною полуплоскостью Oxz. Угол отсчитывается от полуплоскости Oxz в каком-либо определенном направлении, например по направлению движения часовой стрелки (для наблюдателя, стоящего вдоль Oz).
Ясно, что достаточно изменять
в пределах (0,
![]() ),
— в пределах (0, л) и
— в пределах (0, 2л), чтобы получить все
точки пространства.
),
— в пределах (0, л) и
— в пределах (0, 2л), чтобы получить все
точки пространства.
В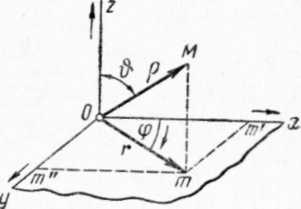 еличины
,
и
называются полярными (или сферическими)
координатами точки М.
еличины
,
и
называются полярными (или сферическими)
координатами точки М.
Найдем теперь формулы перехода от полярных координат к декартовым прямоугольным.
Мы предполагаем (рис), что ось Oz совпадает
с полярною осью. Ох расположена в полярной
полуплоскости, а Оу перпендикулярна к
обеим предыдущим осям и притом проведена
в такую сторону, чтобы угол
для полуплоскости Oyz был равен
![]() .
Имеем, очевидно,
.
Имеем, очевидно,
z = пр![]() ОМ
=
cos
.
ОМ
=
cos
.
Проектируя, далее, вектор ОМ на плоскость
Оху, мы получим вектор
![]() (черт. 63) длины r
(черт. 63) длины r
= = cos ( - ) = sin ,
который составляет с осью Ох угол . Если спроектировать этот вектор на Ох и Оу, то получим
х = | Оm | cos = sin cos ,
у = | Оm | sin = sin sin .
Итак,
х = sin cos , у = sin sin , z = cos . (1)
Обратно, зная х, у, z, можем определить , и .
Полуполярные (цилиндрические) координаты
При обозначениях предыдущего параграфа положение точки М вполне определяется заданием полярных координат (г, ) проекции т точки М на плоскость Оху и координаты z = mМ. Величины г, , z называются полуполярными (или цилиндрическими) координатами точки М.
Переход от этих координат к прямоугольным декартовым дается (при обозначениях предыдущего параграфа) формулами
x = rcos , y = rsin , z = z. (1)
Общий метод координат
Системы декартовых, полярных и полуполярных координат представляют собою только частные случаи осуществления общего метода координат; чтобы дать представление об этом методе, начнем со случая координат на плоскости.
Вообразим на плоскости (черт. 64) две системы линий (кривых или прямых), обладающих тем свойством, что через каждую точку М плоскости проходит по одной и только по одной линии каждой системы и что кроме М эти две линии нигде не пересекаются. Например, мы можем за линии первой и второй систем принять прямые, параллельные соответственно осям Ох и Оу (черт. 65). Упомянутые линии назовем координатными линиями. Предположим, далее, что каждая линия первой системы вполне характеризуется значением некоторого числа р, так что каждому значению р соответствует вполне определенная линия первой системы; пусть, аналогично, линии второй системы характеризуются значениями некоторого числа q. В приведенном выше примере можно принять Р = х, q = у, где х — отрезок, отсекаемый прямой первой системы на оси Ох, а у — отрезок, отсекаемый на оси Оу прямой второй системы; оба эти отрезка мы предполагаем снабженными знаками.
П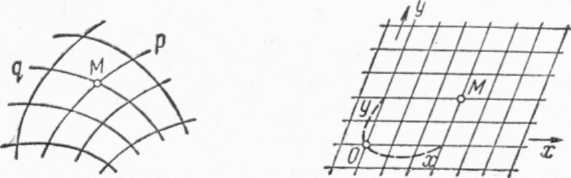 усть
М есть какая-либо точка плоскости; через
нее, по предположению, проходит по
одной линии каждой системы. Числа р и
q, характеризующие эти линии, очевидно,
вполне определяют положение точки
М на плоскости и называются криволинейными
координатами точки М.
усть
М есть какая-либо точка плоскости; через
нее, по предположению, проходит по
одной линии каждой системы. Числа р и
q, характеризующие эти линии, очевидно,
вполне определяют положение точки
М на плоскости и называются криволинейными
координатами точки М.
Если, в частности, за координатные линии мы примем прямые, параллельные двум данным осям Оу и Ох, и за р и q — числа х и у (см. выше), то получим уже известную нам систему необобщенных декартовых координат.
Чтобы прийти к полярным координатам, рассмотрим систему окружностей с общим центром О. Каждая из этих окружностей, которые мы примем за координатные линии первой системы, характеризуется вполне своим радиусом р. За линии второй системы примем полупрямые (лучи), исходящие из точки О; каждая из этих полупрямых вполне определяется углом , составляемым ею с некоторой постоянной осью Ох на плоскости (углу ср мы, как всегда, приписываем определенный знак). Если за р и q принять соответственно р и , то мы придем, очевидно, к полярной системе.
В качестве дальнейшего примера рассмотрим так называемую биполярную систему координат, которую можно определить следующим образом. Возьмем на плоскости две точки О и О'. Примем в качестве линий первой системы окружности с центром в О, а в качестве линий второй системы — окружности с центром в О'. Пусть координатами р и q служат радиусы и ' окружностей первой и второй систем. Иначе говоря, примем за координаты какой-либо точки М расстояния этой точки до двух данных точек О и О'. Полученная система координат называется биполярной. Заметим, впрочем, что координатные линии этой системы не вполне удовлетворяют поставленным выше условиям; линии различных систем пересекаются, вообще говоря, в двух точках; поэтому совокупности значений , ' соответствуют вообще не одна, а две точки. Чтобы устранить это неудобство, можно, например, ограничиться рассмотрением одной из двух частей плоскости, на которые она разбивается прямой OО'.
Заметим еще, что приведенные выше соображения применяются и к определению положения точки на любой поверхности (а не только на плоскости). Простейший пример — общеизвестные географические координаты на сфере. Здесь координатными линиями являются меридианы и параллели, а координатами р и q — долгота и широта.
Предыдущие соображения непосредственно обобщаются на случай пространства трех измерений.
Вообразим в пространстве три системы поверхностей, обладающих тем свойством, что через каждую точку проходит одна и только одна поверхность каждой системы и что эти три поверхности имеют только одну общую (всем трем) точку М. Пусть каждая из поверхностей первой системы характеризуется заданием значений некоторой величины р; аналогично, пусть каждая из поверхностей второй и третьей систем характеризуется заданием некоторой величины q, соответственно r. Рассматриваемые поверхности называются координатными поверхностями, а линии пересечения этих поверхностей — координатными линиями. Ясно, что через каждую точку пространства проходят три координатные линии.
Если дана точка М, то этим самым даны координатные поверхности, проходящие через М, т. е. даны значения величин р, q, r, и обратно. Величины р, q, r называются криволинейными координатами точки М.
Декартовы координаты представляют собою частный случай криволинейных; в этом случае координатные поверхности суть плоскости, параллельные плоскостям координат; роль величин р, q, г выполняют отрезки х, у, r (снабженные знаками), отсекаемые этими плоскостями на осях координат (считая от О), или (в случае обобщенных координат) пропорциональные им величины. Координатные линии суть прямые, параллельные осям координат.
