4.4 Система m уравнений с n неизвестными

Случай, когда число уравнений mбольше числа переменныхn, путем последовательного исключения неизвестных из уравнений приводится к случаюm=nилиmn. Первый случай рассмотрен ранее.

Во втором случае, когда число уравнений меньше числа неизвестных mnи уравнения независимы, выделяютсяm основных переменныхи (n-m)неосновных переменных. Основными являются переменные удовлетворяющие условию: определитель, составленный из коэффициентов при этих переменных, не равен нулю. Основными могут быть различные группы переменных. Общее количество таких групп Nравно числу сочетаний изnэлементов поm:

.

Если система имеет хотя бы одну группу основных переменных, то эта система является неопределенной, то есть имеет множество решений.

Если система не имеет ни одной группы основных переменных, то система является несовместной, то есть не имеет ни одного решения.

В том случае, когда система имеет множество решений, среди них выделяют базисное решение.

Базисным решениемназывают такое решение, в котором неосновные переменные равны нулю. У системы имеется не более чембазисных решений.

Решения системы делятся на допустимыеинедопустимые.

Допустимыминазывают такие решения, у которых значения всех переменных неотрицательны.

Если хотя бы одно значение переменной отрицательно, то решение называют недопустимым.

Пример 4.5

Найти базисные решения системы уравнений

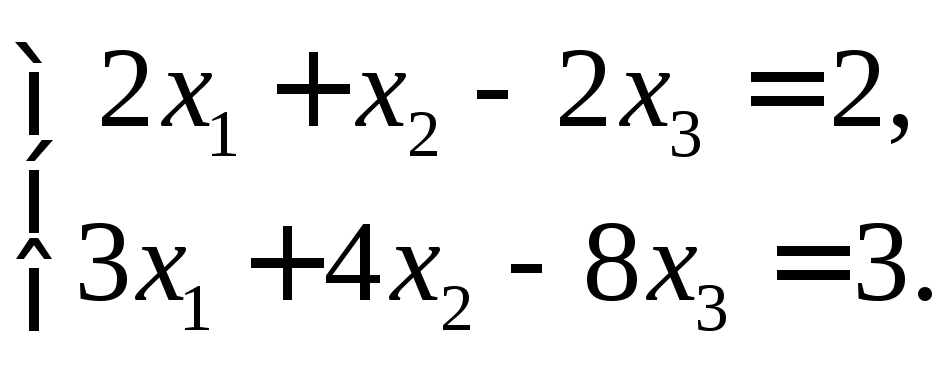
Найдем число базисных решений

.

Итак, среди множества решений системы есть не более трех базисных. Выделим две основные переменные среди трех. Предположим, что это х₁их₂. Проверим определитель из коэффициентов при них

.

Так как этот определитель не равен нулю, то переменные х₁,х₂являются основными.

Теперь положим, что х₃=0. Тогда получим систему в виде

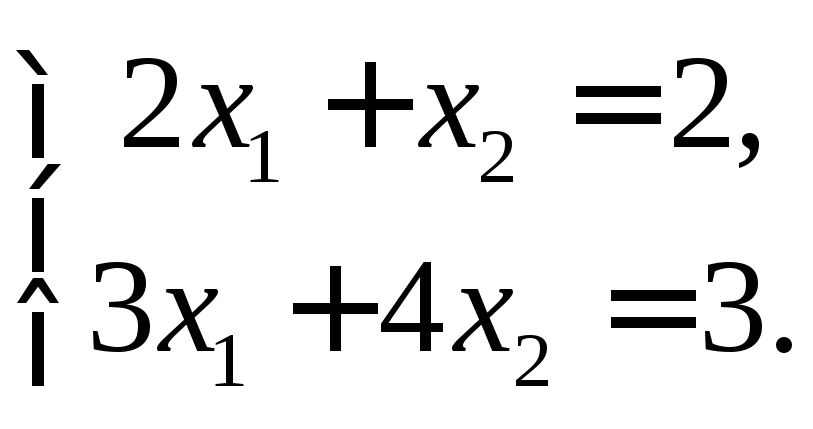
Решим ее по формулам Крамера:

, .

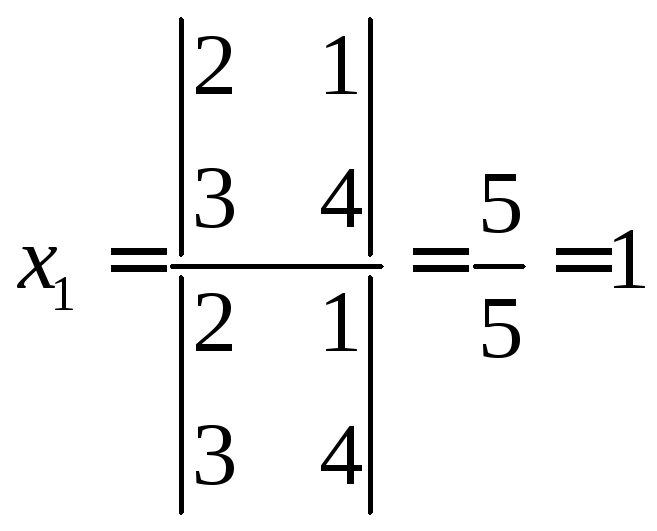Итак, первое базисное решение имеет вид

х₁=1,х₂=0,х₃=0 .

Проверим теперь на принадлежность к основным переменные х₁их₃.

.

Получим, что х₁их₃- вторая группа основных переменных. Положимх₂=0 и решим систему

, .

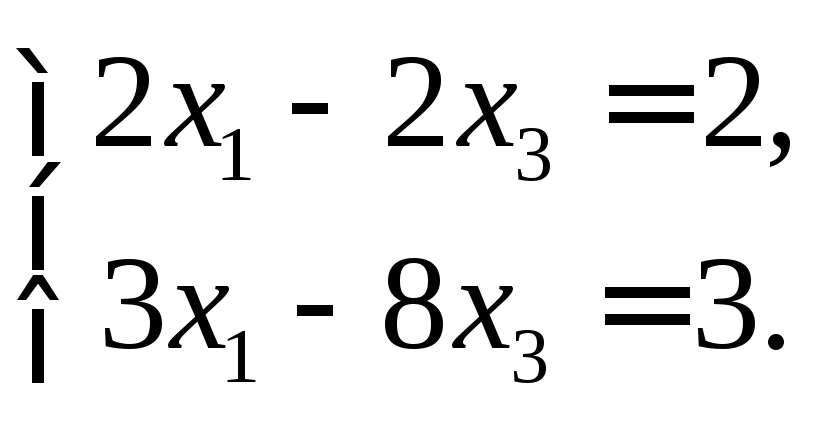
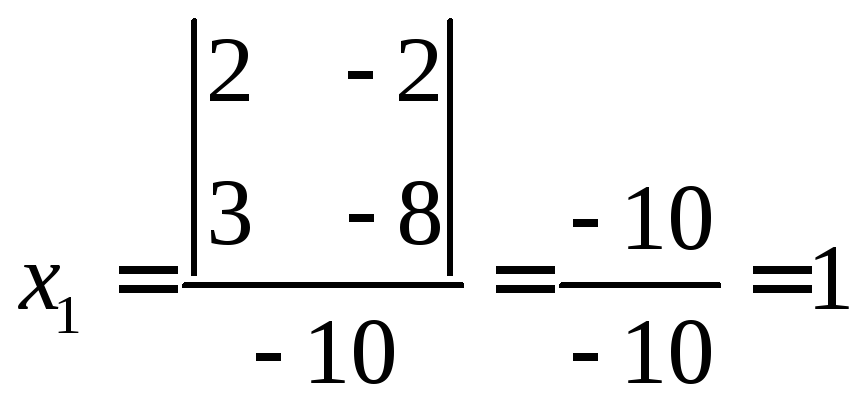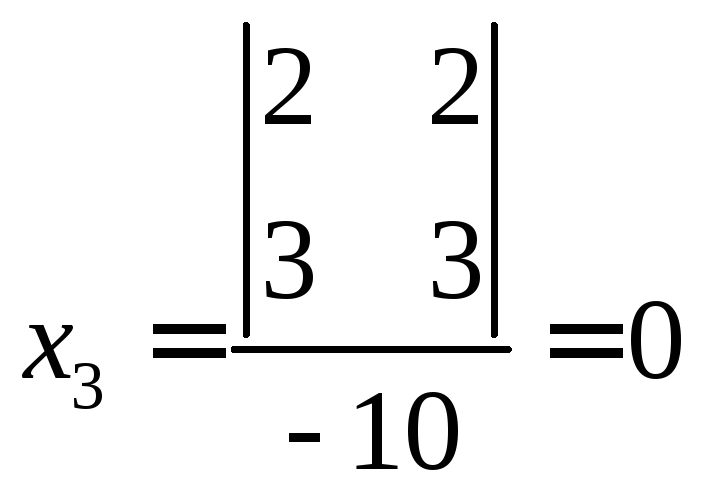Второе базисное решение имеет вид

х₁=1,х₂=0,х₃=0.

Теперь проверим на принадлежность к основным переменные х₂их₃.

то есть переменные х₂их₃неосновные. Итак, всего у данной системы оказалось два базисных решения. Оба эти решения допустимые.

Условие совместности системы mлинейных уравненийcnпеременными дается с помощью понятия ранг матрицы.

Ранг матрицы– это число равное наибольшему порядку минора отличного от нуля.

Для матрицы А

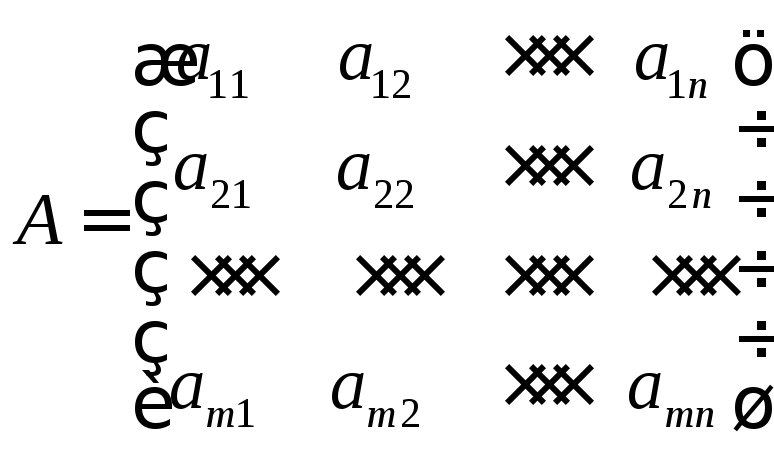
минором k-ого порядкаслужит определитель, составленный из элементов любыхkстрок иkстолбцов.

Например,

Пример 2

Найти ранг матрицы

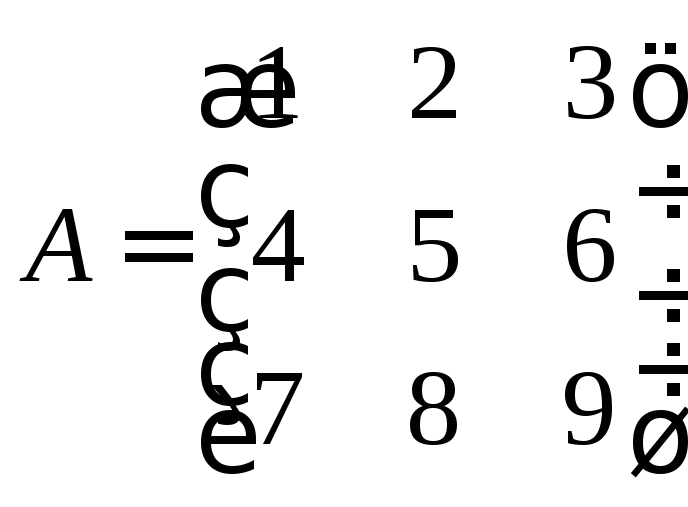
Вычислим определитель матрицы

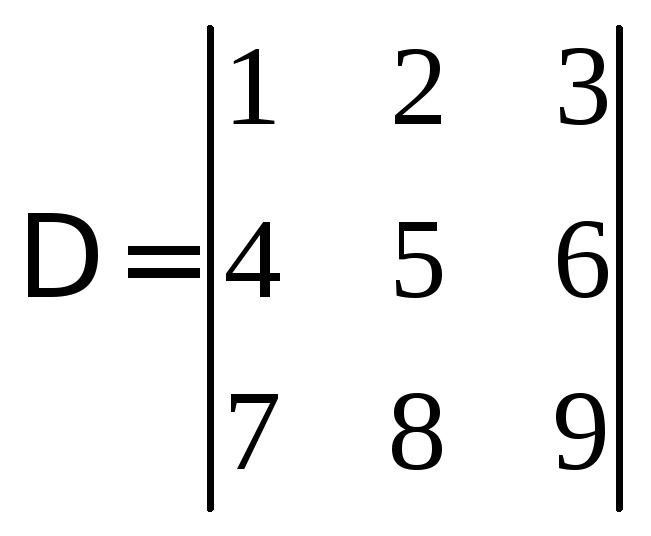
Для этого первую строку умножим на (-4) и сложим со второй строкой, затем первую строку умножим на (-7) и сложим с третей строкой, в результате получим определитель

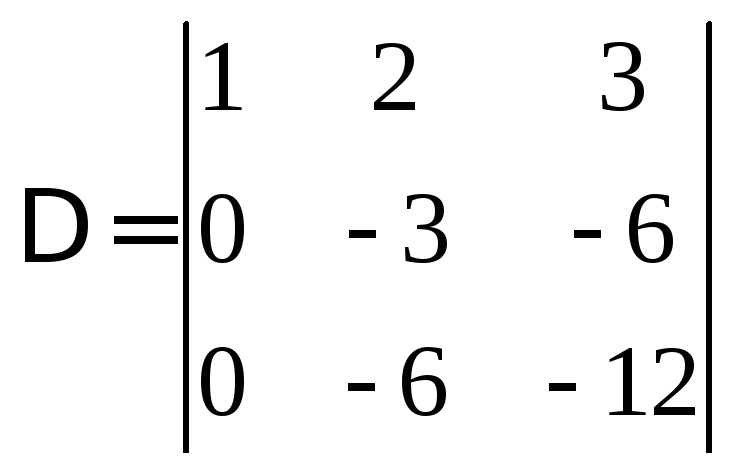
Т.к. строки полученного определителя пропорциональны, то .

Отсюда видно, что минор 3-его порядка равен 0, а минор 2-ого порядка не равен 0.

Следовательно ранг матрицы r=2.

Расширенная матрицасистемы имеет вид

Теорема Кронекера - Капелли

Для того, чтобы линейная система была совместной необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы .

Если _,то система несовместна.

Для совместной системы линейных уравнений возможны три случая:

1)Если , то система ЛУ имеет (m-r) линейно зависимых уравнений, их можно исключить из системы;

2) Если , то система ЛУ имеет единственное решение;

3) Если , то система ЛУ имеет множество решений