§ 7 . Равномерная непрерывность функции на множестве

Пусть функция f(x) определена на множестве X, которое является промежутком или объединением нескольких промежутков.

Определение 1. Функция f(x) называется равномерно непрерывной на множестве X, если такое, что _, удовлетворяющих условию|x₁– x₂|<, выполняется неравенство |f(x₁) – f( x₂)|<.

Если напомнить определение непрерывной на множестве X функции, то в общем случае для любого фиксировнного для каждогоx₁ из X существует свое , такое, что, если |x – x₁|<, то выполняется неравенство |f(x) – f(x₁)|<. В случае равномерной непрерывности для любого фиксированногосуществует общее для всехx из X , для которого выполняется необходимое неравенство. Этим равномерная непрерывность отличается от непрерывности функции на множестве X.

Замечание. Если функция f(x) равномерно непрерывна на множестве X, то она –непрерывная на множестве X.

Для доказательства этого факта достаточно в определении равномерной непрерывности считать x₁= x, x₂= x₀. Получаем:такое, что _, удовлетворяющих неравенству |x – x₀|<, выполняется неравенство |f(x) –f(x₀)|<— это определение непрерывной в любой точкефункции по Коши.

Геометрическая иллюстрация равномерной непрерывности.

Е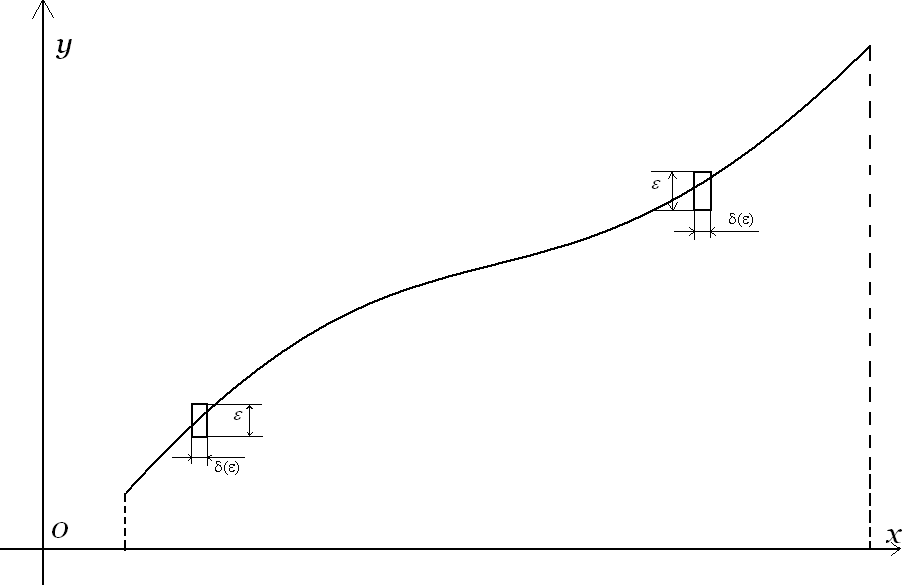сли функцияf(x) равномерно непрерывная на X, то такое, что прямоугольник со сторонамии(стороны прямоугольника параллельны соответственно осямOx и Oy) можно перемещать вдоль графика функции f(x) так, что график не пересечет горизонтальных сторон, а будет пересекать только вертикальные, при сохраняется параллельность сторон осямкоординат (см. рисунок).

Пример 1. Исследовать на равномерную непрерывность функцию на интервале (–a;a) где a>0.

Решение.

Зафиксируем любое число и пакажем, что найдется такое, что для всех , удовлетворяющих неравенству |x₁– x₂|<, выполняется неравенство

|x₁²– x₂²|<. Рассмотрим разность

(x₁²– x₂²)=(x₁– x₂)(x₁ + x₂) и заметим, что если , то модуль суммы

|x₁ + x₂|<2a. С учетом свойства модуля, получаем неравенство

|x₁²– x₂²| = |x₁– x₂ ||x₁ + x₂|<2a|x₁– x₂ |. Потребуем, чтобы 2a|x₁– x₂|<|x₁– x₂|<. Тогда для всех , удовлетворяющих условию |x₁– x₂|<, где=, выполняется неравенство |x₁²– x₂²|<. Так как– любое положительное число, то функцияравномерно непрерывная на интервале (–a;a), по определению.

Пример 2. Доказать, что функция не является равномерно непрерывной на всей числовой прямой.

► Пакажем, что существует такое число , что для всех>0 всегда найдутся _, такие, что| x₁– x₂|<, але |x₁²– x₂²|>. Возьмем=1 и рассмотрим точки

x₁=+иx₂ = , где–любое положительное число, они удовлетворяют неравенству

| x₁– x₂|=|+–|=<, но |x₁²– x₂²| = | x₁– x₂|| x₁+ x₂|=(+)=1+≥1. Значитне является равномерно непрерывной на всей числовой прямой. ◄

Теорема 1.(Кантора) Непрерывная на отрезке является равномерно непрерывной на этом отрезке

Дано: функция f(x)– непрерывная на [a;b].

Докзать: функция. f(x) — равномерно непрерывная на [a;b].

► Доказательство проведем методом от противного. Пусть f(x) не является равномерно непрерывной на [a;b], т.е. ε^* > 0такое, что δ>0и для любых x’_, x” [a;b], удовлетворяющих неравенству |x’– x”|<, выполняется неравенство |f(x’) – f( x”)|≥^*.

Для δ = 1  x₁’_, x₁”[a_, b] такие, что |x₁’– x₁”|<1, выполняется неравенство

|f(x₁’) – f( x₁”)|≥^*.

Для δ = 1 x₂’_, x₂”[a_, b] такие, что |x₂’– x₂”|< , выполняется неравенство

|f(x₂’) – f( x₂”)|≥^*.

Для δ =  x₃’_, x₃”[a_, b] такие, что |x₃’– x₃”|< , выполняется неравенство

|f(x₃’) – f(x₃”)|≥^*.

......................................................................................

Для δ =  x_n’_, x_n”[a_, b] такие, что |x_n’– x_n”|< ,(1)

выполняется неравенство |f(x_n’) – f( x_n”)|≥^*. (2)

......................................................................................

Таким образом на [a_, b] построили две ограниченные последовательности (x_n’)_{, (}x_n”) (по Т § )  – сходящаяся подпоследовательность последовательности (x_n’), и пусть [a_, b]. (3) Адпаведная подпоследовательность последовательности (x_n”) является абмежаванай – збежная подпоследовательность последовательности  – збежная подпоследовательность последовательности и . Из неравенства

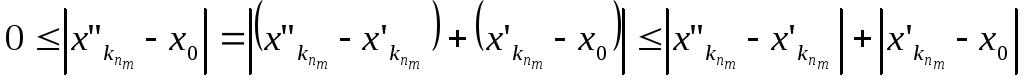
по теореме о пределе промежуточной последовательности, с учетом (1) и (3), получаем, что 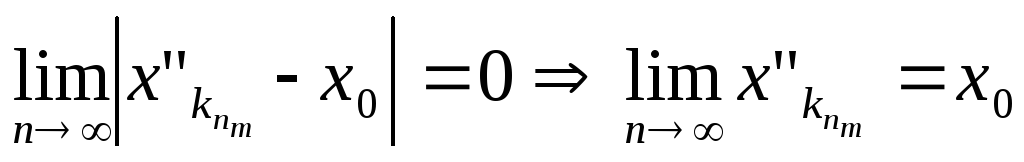[a_, b]. По условию теоремы функция f(x) –непрерывна на [a;b], а значит и в точке х₀. Воспользуемся определением непрерывной функции по Гейне: ,ε>0 (а значит и для ε = ^*.)  n₀N такой, что  n > n₀, nN выполняется неравенство 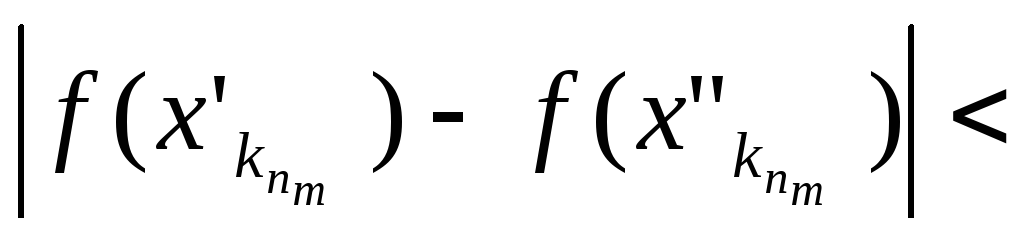^*, что противоречит (2). Полученное противоречие доказывает теорему.◄

Следствие. Если функция f(x) непрерывна на [a,b], тогда такое, что при любом делении [a,b] на части точками a=x₀< x₁<… < x_k–1< x_k<… x_n=b, при условии, что длины отрезков деления меньше , выполняется неравенство

.

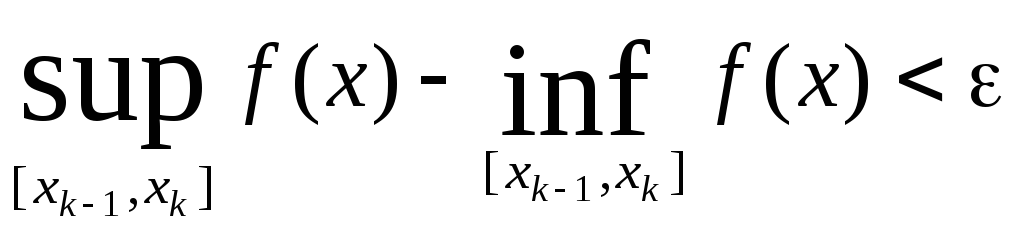Замечание. Если функция f(x) непрерывна на (a,b), то теорема Кантора, вообще говоря, не имеет места.

Пример 3. Функция не является равномерно непрерывной на (0;1). Действительно, дляε >0 δ = minтакое, что  х (0;1), удовлетворяющие условию |x – x₀|<, выполняется неравенство |f(x) –f(x₀)|<— это определение непрерывной в любой точкефункции по Коши. Из формулы для δ видно, что оно зависит отx₀ Пакажем, что ε >0 нельзя подобрать δ такое, чтобы оно было одинаковым для всех х₀ (0;1) и, как только |x – x₀|<, то выполняется неравенство |f(x) –f(x₀)|<. Доказательство проведем методом от противного, пусть дляε>0 такое, что _, удовлетворяющих условию |x₀– x|<, выполняется неравенство |f(x₀) – f( x)|< ε. Возьмем 0<x₀<δ, а потом 0<x<

 , но f(x) – f(x₀)= (противоречие)  нельзя подобрать δ такое, чтобы оно было одинаковым для всех х₀ (0;1).

Определение 2. Величина называетсяколебанием функции f(x) на промежуткеX.

8