
Уравнение плоской электромагнитной волны
При
прохождении монохроматической
электромагнитной
волны
частотой ω векторы E
и H
в данной фиксированной точке пространства
испытывают синфазные и только синфазные
гармонические колебания с этой же
частотой
![]() Из
условия синфазности следует, что в тех
точках пространства, где E
= 0
должно быть и H
= 0,
аналогично и по амплитудным значениям
E0
и H0.
Это значит, что векторная волна
электрического поля E
пространственно совпадает с векторной
волной
магнитного поля H,
но только при этом векторы E
и H
колеблются во взаимно – перпендикулярных
плоскостях, как это показано на рисунке
ниже
Из
условия синфазности следует, что в тех
точках пространства, где E
= 0
должно быть и H
= 0,
аналогично и по амплитудным значениям
E0
и H0.
Это значит, что векторная волна
электрического поля E
пространственно совпадает с векторной
волной
магнитного поля H,
но только при этом векторы E
и H
колеблются во взаимно – перпендикулярных
плоскостях, как это показано на рисунке
ниже
 Если
источником задается одно единственное
направление x
для излучения электромагнитной
волны,
то фронт волны будет плоским,
а волна одномерной, как для вектора E,
так и для вектора H.
В этом случае волну можно представить
двумя уравнениями, соответственно
Если
источником задается одно единственное
направление x
для излучения электромагнитной
волны,
то фронт волны будет плоским,
а волна одномерной, как для вектора E,
так и для вектора H.
В этом случае волну можно представить
двумя уравнениями, соответственно
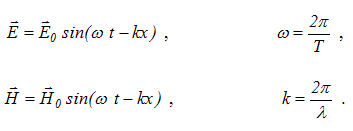
9.
Оптическая
разность хода. Вместо
разности фаз
![]() интерферирующих
волн удобно ввести в рассмотрение
пропорциональную ей величину
интерферирующих
волн удобно ввести в рассмотрение
пропорциональную ей величину
![]() —
оптическую разность хода, которая
отличается множителем
—
оптическую разность хода, которая
отличается множителем
![]() ,
где
,
где
![]() —
длина световой волны.
—
длина световой волны.
![]() Изменению разности фаз на
Изменению разности фаз на ![]() соответствует изменение разности хода
на
соответствует изменение разности хода
на ![]() .
В вакууме оптическая разность хода
в отличие от разности фаз имеет
наглядную интерпретацию. Если две
интерферирующие волны испускаются
одним источником света, то разность
хода — это геометрическая разность
длин путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана. Например, в оптической
схеме опыта Юнга, изображенной на рис.
18, разность хода для точки P на экране
находится по формуле:
.
В вакууме оптическая разность хода
в отличие от разности фаз имеет
наглядную интерпретацию. Если две
интерферирующие волны испускаются
одним источником света, то разность
хода — это геометрическая разность
длин путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана. Например, в оптической
схеме опыта Юнга, изображенной на рис.
18, разность хода для точки P на экране
находится по формуле:![]() .
В изотропной среде скорость света в
.
В изотропной среде скорость света в ![]() раз меньше, чем в вакууме, здесь
раз меньше, чем в вакууме, здесь
![]() —
показатель
преломления среды. Частота света
в среде и в вакууме одинакова,
поэтому длина волны в среде в
—
показатель
преломления среды. Частота света
в среде и в вакууме одинакова,
поэтому длина волны в среде в ![]() раз меньше. В соответствии с соотношением
раз меньше. В соответствии с соотношением
![]() вместо
реального уменьшения длины волны
вместо
реального уменьшения длины волны
![]() можно
рассматривать неизменную
можно
рассматривать неизменную
![]() и соответствующее
увеличение длины пути луча. С этой
целью вводится понятие оптической длины
пути, которая в
и соответствующее
увеличение длины пути луча. С этой
целью вводится понятие оптической длины
пути, которая в ![]() раз больше геометрической длины. Далее,
употребляя термин «разность хода»,
всегда будем иметь в виду оптическую
разность хода. Заменяя разность фаз
интерферирующих волн оптической
разностью хода, получаем следующее
выражение для интенсивности
интерференционной
картины:
раз больше геометрической длины. Далее,
употребляя термин «разность хода»,
всегда будем иметь в виду оптическую
разность хода. Заменяя разность фаз
интерферирующих волн оптической
разностью хода, получаем следующее
выражение для интенсивности
интерференционной
картины:
![]() .
Приемники света в оптическом диапазоне
реагируют на интенсивность
света, а не на напряженность
электрического или магнитного полей.
Поэтому измеряемые в опыте величины,
ширина
полос и видность,
также могут быть выражены через
интенсивность,
а значит и через оптическую разность
хода. Следовательно, понятие оптической
разности хода позволяет свести оптическую
задачу по интерференции
к геометрической задаче отыскания
разности хода. Отметим, что разность
хода лучей можно отсчитывать не только
как разность длин путей от источника
до точки наблюдения, но и как
разность длин путей от двух точек
любой поверхности равной фазы волны
до точки наблюдения. При этом, конечно,
две точки на поверхности равной фазы
— не произвольные точки, а должны
быть точками, через которые реально
проходят лучи, попадающие в точку
наблюдения. Так на рис. 18
.
Приемники света в оптическом диапазоне
реагируют на интенсивность
света, а не на напряженность
электрического или магнитного полей.
Поэтому измеряемые в опыте величины,
ширина
полос и видность,
также могут быть выражены через
интенсивность,
а значит и через оптическую разность
хода. Следовательно, понятие оптической
разности хода позволяет свести оптическую
задачу по интерференции
к геометрической задаче отыскания
разности хода. Отметим, что разность
хода лучей можно отсчитывать не только
как разность длин путей от источника
до точки наблюдения, но и как
разность длин путей от двух точек
любой поверхности равной фазы волны
до точки наблюдения. При этом, конечно,
две точки на поверхности равной фазы
— не произвольные точки, а должны
быть точками, через которые реально
проходят лучи, попадающие в точку
наблюдения. Так на рис. 18 ![]() ,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
![]() .
Этот прием часто используется при
решении задач.
.
Этот прием часто используется при
решении задач.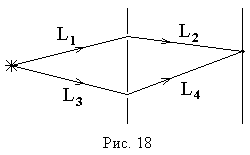
. 10
Дифракция Фраунгофера. Дифракция рассматривает процессы отклонения направления распространения света от прямолинейного при встрече с некоторыми препятствиями или при отражении от них. В случае дифракции Фраунгофера рассматривается падение на препятствие плоской волны (бесконечно удаленный источник света) и подразумевается, что зона наблюдения удалена от препятствия на достаточно большое расстояние (находится на бесконечности). Коротко говоря, это “дифракция в параллельных лучах”. Как Вы увидите, основные задачи дифракции Фраунгофера мы, собственно, уже решили. Просто мы говорили о волнах вообще, а словом дифракция обычно обозначают именно оптические явления, поведение в том или ином случае световой (электромагнитной) волны.
9.1.
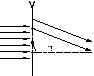
Дифракция на щели. Ранее
мы получили такое выражение для углового
распределения амплитуды от системы
точечных источников, от “цепочки”
источников длиной b: .Ввиду
особой важности да и сложности понимания
этого результата получим его еще раз -
другим способом.
.Ввиду
особой важности да и сложности понимания
этого результата получим его еще раз -
другим способом.
X
b
0
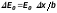 ,
а начальная фаза колебаний зависит от
координаты выбранной полоски:
,
а начальная фаза колебаний зависит от
координаты выбранной полоски:
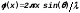 .
Таким образом, разность фаз колебаний
от соседних элементарных полосок шириной
x
составит
.
Таким образом, разность фаз колебаний
от соседних элементарных полосок шириной
x
составит
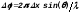 .
На такой угол будут повернуты по отношению
друг к другу соответствующие векторы
на фазовой диаграмме.
.
На такой угол будут повернуты по отношению
друг к другу соответствующие векторы
на фазовой диаграмме.
E
R
E0
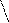

 .
.
При изменении угла угловые размеры дуги изменяется. Но длина дуги, равная сумме модулей (длин) элементарных векторов, считается постоянной:
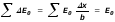 .
.
Это позволяет нам определить радиус дуги и амплитуду суммарных колебаний (см. рисунок) при произвольном :
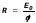 ;
;
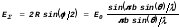 .
.
Как видите, мы получили то же выражение, что и раньше. Но векторная диаграмма позволяет нам нагляднее представить причины обращения амплитуды суммарных колебаний в нуль и достижение максимумов.
При дуга превращается в окружность, амплитуда суммарных колебаний равна нулю. Максимумы достигаются при и, (приблизительно) при 2k.
1
2
E
3
E
E0
E0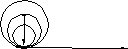
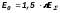 .
Затем спираль становится “двойной
окружностью”, амплитуда колебаний
снова обращается в нуль (3)
и т.д.
.
Затем спираль становится “двойной
окружностью”, амплитуда колебаний
снова обращается в нуль (3)
и т.д.
