
- •Глава 6. Производные и дифференциалы
- •§ 6.1. Производная и её основные свойства
- •6.1.1. Дифференцируемость функции
- •6.1.2.Производная
- •6.1.3. Касательная к графику функции
- •§ 6.2. Вычисление производных
- •6.2.2. Производные элементарных функций
- •6.2.3. Производная обратной функции
- •6.2.4. Производные обратных тригонометрических функций
- •6.2.5. Производная сложной функции
- •6.2.6. Производная функции, заданной параметрически
- •§6.3. Дифференциал
- •6.3.1.Понятие дифференциала числовой функции
- •6.3.2. Геометрический и механический смысл дифференциала
- •6.3.3. Инвариантность формы первого дифференциала
- •6.3.4.Дифференциал суммы, произведения и частного функций
- •§6.4. Производные и дифференциалы высших порядков
- •6.4.1. Последовательные производные
- •6.4.3. Линейное свойство производных высших порядков
- •6.4.5. Вторая производная функции , заданной параметрически
- •6.4.6. Дифференциалы высших порядков
- •§ 6.5. Эластичность и её свойства
6.2.2. Производные элементарных функций
.
1.Производная
степенной функции
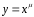 ,
(где
,
(где − любое вещественное число).
− любое вещественное число).
Область
определения этой функции зависит от
 .
Произведём рассуждения, предполагая,
что
.
Произведём рассуждения, предполагая,
что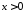 ,
хотя
аналогичные рассуждения справедливы
в естественной области определения
рассматриваемой функции. Имеем
(при
,
хотя
аналогичные рассуждения справедливы
в естественной области определения
рассматриваемой функции. Имеем
(при
 )
)
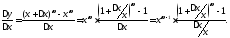 .
.
При
 пользуясь пределом
пользуясь пределом
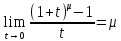 ,
,
вычисленным
в теореме 4.8 ,получим, полагая
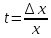 и замечая, что при такой замене выполнены
условия теоремы о пределе сложной
функции,
и замечая, что при такой замене выполнены
условия теоремы о пределе сложной
функции,
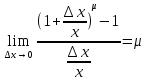 .
Следовательно,
.
Следовательно,
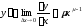 .
.
2.Производная
показательной функции
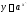 (
( ,
,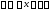 ).
Здесь
).
Здесь
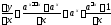 .
.
Используя предел
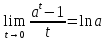 ,
,
вычисленный в теореме 4.8, найдём:
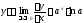 .
.
В
частности, если
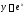 ,
то и
,
то и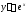 .
.
Таким
образом, скорость возрастания показательной
функции ( при
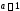 )
пропорциональна значению самой функции.
Это характеризует рост показательной
функции.
)
пропорциональна значению самой функции.
Это характеризует рост показательной
функции.
3.
Производная логарифмической
функции
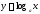 (
(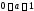 ,
,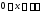 ).
В этом случае
).
В этом случае
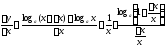 .
.
Воспользуемся пределом
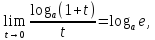
вычисленным в теореме 4.8:
 .
.
Для натурального логарифма получается совсем простая формула:
при
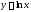 имеем
имеем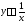 .
.
4.Производные
тригонометрических функций.
Пусть
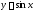 ,
тогда
,
тогда
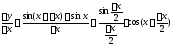 .
.
Функция
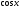 непрерывна, кроме того,
непрерывна, кроме того,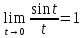 , поэтому
, поэтому
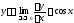 .
.
Аналогично,
если
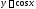 ,
то
,
то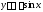 .
.
В
случае
 применима теорема 6.2.1 , по которой
применима теорема 6.2.1 , по которой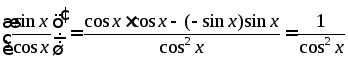
Аналогично,
если
 ,
то
,
то![]() .
.
6.2.3. Производная обратной функции
Докажем следующую общую теорему.
Теорема
6.2.2.
Пусть
функция
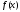 возрастает(или убывает) и непрерывна
на некотором промежутке и в точке
возрастает(или убывает) и непрерывна
на некотором промежутке и в точке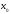 этого
промежутка имеет иотличную
от нуля
производную
этого
промежутка имеет иотличную
от нуля
производную
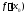 .
Тогда для обратной функции
.
Тогда для обратной функции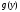 в соответствующей точке
в соответствующей точке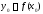 также существует производная, равная
также существует производная, равная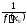 .
.
Доказательство.
Придадим значению
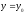 приращение
приращение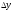 ,
тогда соответствующее приращение
,
тогда соответствующее приращение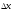 получит и функция
получит и функция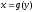 .
При
.
При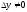 ,
ввиду монотонности функции
,
ввиду монотонности функции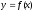 ,
также и
,
также и .
Поэтому
.
Поэтому
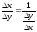 .
.
Если
теперь
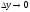 ,
то, вследствие непрерывности функции
,
то, вследствие непрерывности функции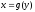 , также и
, также и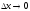 .
Но знаменатель правой части стремится
к пределу
.
Но знаменатель правой части стремится
к пределу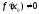 ,
следовательно, существует предел и для
левой части, равный обратной величине
,
следовательно, существует предел и для
левой части, равный обратной величине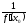 .
По определению, он равен производной
.
По определению, он равен производной .
.
Итак,
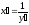 .
.
Легко
выяснить геометрический
смысл этой формулы.
Производная
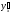 есть тангенс угла
есть тангенс угла ,
образованного касательной к графику
функции
,
образованного касательной к графику
функции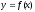 с осью
с осью .
График обратной функции
.
График обратной функции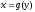 совпадает
с графиком функции
совпадает
с графиком функции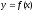 и
имеет ту же касательную. Поэтому
производная
и
имеет ту же касательную. Поэтому
производная равна тангенсу угла
равна тангенсу угла![]()
![]() ,
составленного той же касательной с
осью
,
составленного той же касательной с
осью (см. рис.) Таким образом, выведенная
формула означает, что
(см. рис.) Таким образом, выведенная
формула означает, что
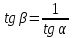 .
.

![]() .
.
Рассмотрим,
например, функцию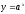 .
Обратной для неё функцией является
.
Обратной для неё функцией является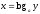 .
Так как
.
Так как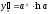 ,
то
,
то
 ,
что и было установлено в 6.2.2 другим
способом.
,
что и было установлено в 6.2.2 другим
способом.
Доказанная
формула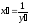 равносильна формуле
равносильна формуле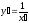 .
.
6.2.4. Производные обратных тригонометрических функций
Рассмотрим
функцию
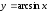 (
(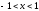 ).
Для неё выполнены неравенства
).
Для неё выполнены неравенства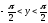 .
Она является обратной для функции
.
Она является обратной для функции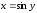 ,
имеющей для указанных значений
,
имеющей для указанных значений положительную производную
положительную производную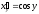 .
В таком случае существует также
производная
.
В таком случае существует также
производная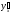 и равна, по нашей формуле,
и равна, по нашей формуле,
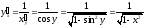 ;
;
корень
мы берем со знаком плюс, так как при
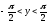 выполняется
неравенство
выполняется
неравенство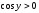 .
Мы исключили значения
.
Мы исключили значения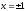 ,
ибо для соответствующих значений
,
ибо для соответствующих значений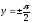 производная
производная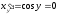 .
.
Функция
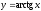 (
(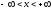 )
служит обратной для функций
)
служит обратной для функций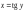 .
По нашей формуле
.
По нашей формуле
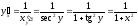 .
.
Аналогично можно получить:
производная
функции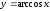 равна
равна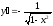 (
(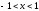 ),
),
производная
функции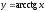 равна
равна (
( ).
).
6.2.5. Производная сложной функции
Теорема
6.2.3.(Теорема
о производной сложной функции). Пусть
функция
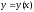 определена в окрестности точки
определена в окрестности точки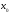 и имеет в этой точке производную
и имеет в этой точке производную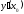 .
Пусть функция
.
Пусть функция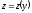 определена в окрестности
определена в окрестности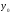 и имеет в точке
и имеет в точке производную
производную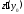
Тогда
сложная функция
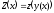 имеет производную, равную
имеет производную, равную
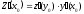 .
.
Доказательство.
Придадим
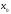 приращение
приращение такое, что соответствующее значение
такое, что соответствующее значение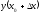 принадлежит окрестности точки
принадлежит окрестности точки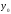 ,
в которой определена функция
,
в которой определена функция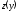 .
Так как
.
Так как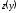 ,
по условию, дифференцируема в точке
,
по условию, дифференцируема в точке ,
,
 ,
где
,
где
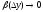 при
при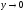 и
и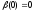 .
.
Так
как
 дифференцируема в точке
дифференцируема в точке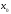 ,
выполнено равенство
,
выполнено равенство
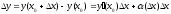 ,где
,где
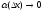
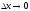 .
Как установлено в теореме 6.1.1, если
.
Как установлено в теореме 6.1.1, если ,
то и
,
то и .
.
Поэтому
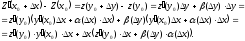
Так
как при
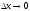 и
и ,функции
,функции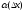 ,
,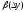 −бесконечно
малые, из этого равенства следует, что
−бесконечно
малые, из этого равенства следует, что
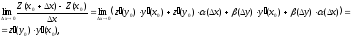 что
и требовалось доказать.
что
и требовалось доказать.
