Типовые задачи c решениями

Задачи по теории функций комплексного переменного Часть 2

На дневном, на вечернем и на заочном отделениях факультета прикладной математики-процессов управления Санкт-Петербургского государственного университета читается годовой курс по Теории функций комплексного переменого (ТФКП). Программа этого курса приведена на сайте факультета http://www.apmath.spbu.ru/ru/staff/starkov/. Там же помещена первая часть курса.

При составлении методических указаний использовались различные источники, список которых приведен.

В каждом пункте даются краткие сведения теоретического характера с целью сделать читателя менее зависимым от наличия или отсутствия у него соответствующей литературы. Для некоторых задач решение доведено до конца, для других даются указания к решению, для всех задач приведены ответы.

Содержание

1.Интегрирование функций комплексного переменного

1.1.Вычисление интегралов по формуле Ньютона-Лейбница

1.2.Интеграл по контуру

1.3.Интегральная формула Коши

2.Ряды

2.1.Степенные ряды и ряд Тейлора

2.2.Ряд Лорана

3.Изолированные особые точки и вычеты функций

3.1.Классификация особых точек

3.2.Вычеты функций

4.Применение вычетов к вычислению интегралов

4.1.Вычисление интегралов на основе теоремы Коши

4.2.Вычисление определенных интегралов с помощью вычетов

4.3.Несобственные интегралы от действительной переменной

5.Тестирование по пройденному материалу

6.Литература

1.Интегрирование функций комплексного переменного

1.1.Вычисление интегралов по формуле Ньютона-Лейбница

Функция F(z) называется первообразной функцией для f (z) , если F′(z) = f (z) . Если функция f (z) является аналитической в односвязной области D, то интеграл от f (z) по любому пути, соединяющему точки z1 и z2 этой области и лежащему в ней, равен разности значений первообразной в точках z2 и z1 , т.е. вычисляется по известной формуле Ньютона-Лейбница. Интегралы от элементарных функций

комплексного переменного вычисляются с помощью тех же формул, что и для функций вещественной переменной.

i	1+πi	1+i
1. Вычислить интегралы: а) ò z cos zdz , б)	ò ze−z dz ,	в) ò z2dz .
0	0	0

	Ответ: а)	1	−1, б)	1	(2 + πi) ,	в)	2	(−1+ i) .
		e		e			3

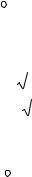
i

1+i

π +i

dz

2

2. Вычислить интегралы: а) ò zez dz ,

б) ò

,

в)

òsin zdz .

z

0

1

0

Ответ: а) (1− cos1− sin1) + i(cos1− sin1) ,

1

p

i

æ

1

ö

б)

ln 2 +

i , в) 1

+

çe -

÷ .

2

4

2

e

è

ø

1.2.Интеграл по контуру

Если f (z) = u(x, y) + iv(x, y) , то интеграл по дуге АВ,					лежащей	в плоскости z ,	вычисляется	по
формуле	ò f (z)dz = òudx - vdy + i òvdx + udy , т.			е.	представляется как сумма криволинейных
	AB	AB	AB
интегралов от вещественной переменной.
При параметрическом задании дуги АВ: z(t) = x(t) + iy(t) , t1 < t < t2						имеем
	t2	¢
			Это удобно для случая,	когда дуга		является частью	окружности,	а
ò f (z)dz =ò f (z(t))z (t)dt .
AB	t1

параметром служит полярный угол.

Если функция f (z) аналитична в некоторой односвязной области D, то интеграл по любому контуру в

этой области не зависит от пути интегрирования, а вдоль замкнутого контура равен нулю (теорема Коши для односвязной области).

Если функция f (z) есть аналитическая функция в замкнутой многосвязной области, то интеграл по

внешнему контуру равен сумме интегралов по внутренним контурам (теорема Коши для многосвязной области). Везде интегрирование как по внешнему, так и по внутренним контурам совершается в положительном направлении, т.е. так, что область остается все время слева.

3.

Вычислить òIm zdz , где С — прямолинейный отрезок, соединяющий точку 0 с точкой 2 + i.

С

Ответ:

1 + 0, 5i.

4. Вычислить ò

dz

, где С — окружность

z

=1.

z

C

Ответ: 2pi .

dz

5.

Вычислить ò

, где С — верхняя половина окружности

z

=1, направление обхода: от точки (1,0)

С

z

до точки (—1,0) (

взять из общей формулы при k = 0).

z

Ответ:

2(i – 1).

dz

6.

Вычислить ò

, где С — граница области 1<

z

< 2 .

C

z

Ответ:

4

.

3

=1, 0 £ arg z £ p .

7.

Вычислить ò z3dz , где С — четверть окружности

z

С

2

Ответ:

0.

8.

Вычислить òi

z

dz вдоль полуокружности

z

=1,

Re z ³ 0 .

−i

Ответ: 2i.

9.

Вычислить интегралы вдоль кривой С — части окружности

z

= 2 , лежащей в полуплоскости

Im z £ 0 и пробегаемой от точки z1 = -2 до точки z2 = 2 в случаях:

f (ξ)dξ

а) ò		z		dz	б) ò z			z		dz в) ò(2x − 3iy)dz
С					С					С
Ответ: а) 4πi ,						б) 0; в) 10πi .

10.Вычислить интегралы вдоль С — отрезка прямой с началом в z1 =1 и концом в z2 = i от

следующих функций: а) z ,

б)

Im z , в)

z

−1 .

1−i

ln(3 + 2

Ответ: а) i,

б) 0,5(–1 + i);

в)

2) .

2

11. Вычислить интегралы по замкнутому контуру: а)

ò zzdz , б)

ò z Im(z2 )dz , в)

òRe zdz .

б) −16π , в)

я

=1

я

=2

я−1

=1

Ответ: а) 0;

πi .

12. Вычислить интеграл òi

dz

, вдоль дуги параболы y2

= x +1.

−i

z

Ответ: − πi .

13.	Вычислить ò( y + xi)dz , где С — ломаная ОАВ с вершинами в точках zO = 0 , zA = i , zB =1+ i .
		С
Ответ:		0,5 + i.
			x	2	2
14.	Вычислить интеграл ò z10dz , где С — эллипс				+	y	=1.
				2		2
		С	a			b
Ответ:		0.

1.3Интегральная формула Коши

Пусть функция f (z) аналитична в замкнутой области D (односвязной или многосвязной) и Г — граница области D. Оказывается, что тогда значения функции f (z) в любой точке области D можно вычислить, зная только значения f (z) на границе области по интегральной формуле Коши:

f (z) =	1	ò	f (ξ)dξ	.
	2πi		ξ − z
		Γ

Заметим, что формула Коши остается в силе и для многосвязной области, но под интегралом подразумевается сумма интегралов по всем кривым, составляющим контур (обходимые области остаются слева).

Известно, что аналитическая в данной области функция f (z) имеет в этой области производную любого порядка. Производная определяется по формуле

f (n) (z) = 2nπ!i òΓ (ξ − z)n+1 .

С помощью этих формул можно вычислять некоторые криволинейные интегралы по замкнутым контурам для подынтегральной функции специального вида. Формулы следует записать в обратном

порядке

ò	f (ξ)dξ	= 2πif (z) ,	ò	f (ξ)dξ		=			2πi	f (n) (z) .
	ξ − z			n+1
Γ			Γ	(ξ − z)					n!
Пример 1. Вычислить интеграл ò								ez dz			, где С — окружность с радиусом 3/2 и центром в точке 2.
							z(z − 3)
				C

Решение. В качестве числителя подынтегрального выражения в интегральной формуле Коши следует

взять функцию f (z) =

ez

,

которая аналитична в круге,

ограниченном С. Применяя интегральную

z

2πe3i

формулу Коши, получим

ò

ez dz

= ò

f (z)dz

= 2πif (3) =

.

z(z − 3)

z − 3

3

C

C

Пример 2. Вычислить ò

ez dz

.

3

C (z − i)

где С — произвольный замкнутый контур, однократно обходящий точку i в положительном направлении.

Решение.

Функция

f (z) = ez

аналитична в области,

ограниченной контуром С и в силу формулы для

производной, находим

ò

ez dz

=

2πi

f ′′(i) = −πsin1+ iπcos1.

(z − i)

3

C

2!

15. Вычислить интеграл

ò

2z3 +1

dz .

4

z−2

=2

(z −1)

Ответ: 4πi .

dz

16. Вычислить

ò

, если: а) точка 3i лежит внутри контура С, а точка –3i — вне его, б) точка –3i

z

2

+ 9

C

лежит внутри контура С, а точка 3i — вне его.

Ответ: а)

π ,

б) −

π .

3

3

17. Применяя формулу Коши,

вычислить интегралы: а)

ò

z

3dz

,

б) ò

zdz

,

где С— окружность с

z −

1

z

4

−1

центром в точке 2

и радиусом 2.

C

C

Ответ: а) 2πi ; б)

π i .

2

18. Вычислить интегралы по окружностям: а) ò

z2dz

, б)

ò

sin z

dz ,

в)

ò

zdz

.

z + i

z

z

2

−1

z

=2

z−1

=2

z+2

=2

Ответ: а) − 2πi , б) 0;

в) πi .

2 Ряды

2.1Степенные ряды и ряд Тейлора

Различают числовые и функциональные ряды. Из всевозможных функциональных рядов большое распространение имеют степенные ряды:

	∞
	åcn zn = c0 + c1z + c2 z2 +...+ cn zn +...
	n=0
							cn
	Радиус сходимости К можно определить, пользуясь признаками Даламбера или Коши: R = lim							,
						c
					n→∞
							n+1
	R = lim		1		.
	n→∞ n		c
			n

Ряд сходится при z < R , т.е. в круге радиусом R . Более общий вид степенного ряда — ряд Тейлора

∞

1

f (z) = åcn (z − z0 )n , cn =

f (n) (z0 ) .

n!

n=0

Кругом сходимости этого ряда является круг

z − z0

< R .

∞

Пример 1. Рассмотрим геометрическую прогрессию åzn = 1+ z + z2 + ...+ zn + ...

n=0

Ее круг сходимости

z

< 1. Внутри этого круга прогрессия сходится абсолютно, а во всяком замкнутом

круге

z

≤ q < 1–равномерно.

Как и в действительном анализе,

сумма прогрессии внутри ее круга

сходимости равна функции

1

. Эта функция и ее представление рядом очень полезно в задачах

1

− z

разложения в ряды.

z −1

−1)

∞

n

(z

2

Пример 2. Исследовать сходимость ряда å

(z −1)

= 1+

+

+ ...

2!

n=0

n!

1!

cn

Его радиус сходимости равен R = lim

= lim(n +1) = ∞ .

cn+1

n→∞

n→∞

Следовательно, кругом сходимости данного ряда будет вся плоскость z.

Как и в действительном анализе, имеют место разложения при z0 = 0 следующих функций:

∞

z

n

z

z

2

z

n

∞

z

2n+1

z

3

z

5

ez = å

=1+

+

+ ...+

+...,sin z = å(−1)n

= z −

+

−...+

n!

n!

(2n +1)!

n=0

1!

2!

n=0

3!

5!

∞

z

2n

z

2

z

4

z

2n

cos z = å(−1)n

= 1−

+

−...+ (−1)n

+ ...,

(2n)!

(2n)!

n=0

2!

4!

(1+ z)n

=1+ nz +

n(n −1)

z2 + ...+

n(n −1)...(n − k +1)

zk + ...,

2!

k!

∞

z

n

z

z

2

z

3

z

n

ln(1+ z) = å(−1)n

=

−

+

−...+ (−1)n

+ ...

n

2

3

n=1

1

n

Радиус сходимости первых трех рядов R = ∞ , а последних двух R = 1.

∞

19. Определить радиус сходимости степенного ряда åсn zn , если: а) сn = nn , б)

n=1

в) cn = 2nn , г) cn = cos(in) .

z2n+1

(−1)n (2n +1)! + ...,

cn = n1! ,

Ответ: а) 0; б) ∞ , в) 2; г)

1

.

e

∞

z

n

∞

20. Найти круг сходимости рядов: а) 1+ å

,

б) ån!zn ,

n!

n=1

n=1

Ответ: а) R = ∞ , вся плоскость,

б) R = 0 , точка z = 0 ,

в)

∞

n

21. Найти радиус сходимости степенного рядов: а) å

n!z

,

n

n=1 n

Ответ: а) R = e , б) R =

2

.

2

∞

(z − i)

n

в) å

.

2

n

n=1

n (1+ i)

R =

z − i

<

.

2,

2

∞

(1+ i)

n

б) å

(z − 2)n .

(n +1)(n + 2)

n=1

∞	(z + i)	n	∞
22. Найти круг сходимости следующих степенных рядов: а) å			, б) å[2 + (−1)n ]zn ,
	1+ in
n=0			n=0

∞

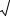
n

∞

в) å

(z +1+ i)

,

г)

å(sin(in))zn .

n

]

n

n=0 [3+ 4×(-1)

n=1

1

Ответ:

а)

z + i

<1

,

б)

z

<1,

в)

z +1+ i

<1,

г)

z

<

.

e

∞

∞

∞

n

23. Определить область сходимости рядов: а)

åez lnn

, б) å

sin nz

,

в)

å

(-1)

.

n=2

n=1

n

n=0 z + n

Ответ:

а) Полуплоскость

Re z < −1, б)

действительная

ось;

в)

вся

плоскость, кроме точек

z = 0,±1,±2,...

∞

æ

n

1

ö

∞

æ zn

n

2 ö

24. Найти область сходимости данных рядов: а)

å

ç z

+

÷ ,

б)

ç

+

÷

,

n

n

è

2

z

ø

åç

n ÷

n=0

n=0

è n! z

ø

∞ é z(z + n)ùn

в) åê

ú .

n

n 1 ë

û

=

Ответ:

а) Кольцо

1

<

z

<1, б)

внешность единичного

круга

z

>1,

в)

z

<1.

2

∞

2n

∞

zn

∞

zn

25. Найти область сходимости данных рядов: а) å

, б)

å

, в) å

.

z

2n

1- z

n

1- z

2n

n=0

+1

n=1

n=1

Ответ:

а)

z

>1, б)

z

<1, в) вся

плоскость, кроме

окружности

z

=1.

26. Разложить

в ряд Тейлора

по степеням z −i функцию

f (z) = z5 .

Ответ:

f (z) = i + 5(z - i) -10i(z -i)2 -10(z - i)3 + 5i(z -i)4 + (z - i)5 .

27. Разложить функции в ряд Тейлора в окрестности точки z0 и указать область сходимости:

а) ln z ,

z0 =1, б) (1- z)ez ,

z0 = 0 , в)

sin 2z − 2sin z , z0 = 0 .

∞

(z -1)

n

∞

nz

n+1

Ответ:

а) ln z = å(-1)n−1

,

z -1

<1, б) 1- å

,

z

< ¥ ,

n

(n +

n=1

n=1

1)!

∞

2 - 2

2n+1

в) å(-1)n+1

z2n+2 ,

z

< ¥ .

(2n +1)!

n=1

∞

1

28. Разложить функции в степенной ряд åсn zn и найти радиус сходимости: а)

, b ¹ 0 ,

az + b

n=0

z

z2

б)

, в)

.

z2 - 4z +13

(z +1)2

∞

n n

∞

n

Ответ: а) å(-1)n

a z

, R =

b

,

б)

i

å[(2 -3i)n - (2 + 3i)n ]

z

, R =

13

,

n+1

a

n

∞

n=0

b

6 n=1

13

в) å(-1)n (n -1)zn , R =1.

n=2

∞

29.

Разложить указанные функции в степенные ряды

åсn zn , используя известные разложения:

в) òz

n=0

а)

ln(z2 - 3z + 2) ,

б) ln

1+ z

,

sin z

dz .

1- z

0

z

∞

z

n

∞

z

2n+1

∞

z

2n+1

Ответ:

а) ln 2 - å(1+ 2−n )

, R =1,

б)

2å

, R =1,

в) å(-1)n

, R = ¥ .

2n +1

(2n +1)!(2n +1)

n=1

n

n=0

n=0

z

30. Разложить указанные функции в ряд по степеням z −1 и найти радиус сходимости: а)

,

z + 2

б)

z

, в)

z2

.

z2 - 2z + 5

(z +1)2

1

∞

(z -1)n

1

∞

(z -1)n

Ответ:

а)

+ 2å(-1)n+1

, R = 3,

б)

å

, R = 2 ,

n

1

n 1

3

n=1

3

+1

4 n=0 2n+

[1+(−1)

+ ]

2

1

∞

n (n -3)(z -1)n

в)

+ å(-1)

, R = 2 .

4

2

n+2

n=1

31.

Функцию sin(2z - z2 ) разложить в ряд по степеням z −1, найти радиус сходимости ряда.

∞

1

æ

np ö

2n

Ответ:

å

sinç1

+

÷(z -

1)

, R

= ¥ .

n!

2

n=0

è

ø

32. Разложить в ряд Тейлора функцию f (z) = ln z

в окрестности z0 = 2 .

∞

n

Ответ:

ln 2 + å(-1)n−1

(z - 2)

, R = 2 .

n

n=1

n2

2.2.

Ряд Лорана

Ряд,

содержащий,

кроме

положительных степеней

z - z0 , также и

отрицательные

степени

z - z0 ,

называется рядом Лорана и имеет вид

∞

a−n

a−1

åan (z - z0 )n = ...+

+...+

+ a0 + a1(z - z0 ) +...+ an (z - z0 )n +...

(z

- z0 )

n

z

n=−∞

- z0

Областью

сходимости

ряда

Лорана

является

круговое

кольцо

R1 <

z - z0

< R2 (кольцо

может

выродиться в кольцо с выколотым центром: 0 <

z - z0

< R2 или во внешность круга с выколотой точкой

z = ∞ :

R1 <

z - z0

< ¥ ,

а также во всю плоскость с двумя выколотыми точками:

0 <

z - z0

< ¥ ).

Часть ряда Лорана с коэффициентами a−n называется главной частью ряда Лорана, а с коэффициентами an — правильной частью.

Всякая аналитическая функция f (z) внутри кругового кольца R1 < z - z0 < R2 может быть разложена

внутри этого кольца в ряд Лорана и притом единственным образом. Коэффициенты ряда Лорана

вычисляются при помощи формулы

	1	ò	f (z)		n = 0,±1,±2,...,
an =				dz,
	2pi		(z -z )n+1
		C	0

где С — любой замкнутый контур, расположенный внутри кольца и окружающий точку z0 .

Однако на практике для вычисления коэффициентов иногда удобнее использовать представление разлагаемой функции в виде суммы функций, каждую из которых можно непосредственно представить в

виде разложения по отрицательным или положительным степеням z - z0 .

Пример. Рассмотрим функцию f (z) =	1	. Она имеет две особые точки	z =1 и z = 2 и,
	(z -1)(z - 2)

значит, в кольце 1< z < 2 является аналитической и разлагается в ряд Лорана. Найдем это разложение, представив функцию в виде суммы простейших дробей:

1

=

1

-

1

.

(z -1)(z - 2)

z

- 2

z -1

Дробь

1

является аналитической

функцией

в круге

z

< 2 и разлагается

z

- 2

степеням аналогично ряду геометрической прогрессии:

æ

ö

ön

1

ç

1

÷

1

æ

z

z2

zn

ö

1

∞ æ z

-

ç

÷

= -

ç1+

+

+...+

+...÷

= -

ç

÷ .

2

z

2

2

22

2n

2

ç

÷

ç

÷

ån 0 è 2

ø

ç1

-

÷

è

ø

=

2

è

ø

Дробь -

1

является аналитической вне круга

z

>1и разлагается по степеням

z -1

по положительным

1z также как сумма

1

1

1

æ

1

1

1

ö

∞ 1

геометрической прогрессии: -

= -

= -

ç1+

+

+...+

+...÷

= -å

-

æ

1

ö

2

n

n

z

1

z è

z z

z

ø

n=1 z

zç1

-

÷

z

è

ø

1

∞

æ z

ön

∞

1

1

∞

é zn

1 ù

Окончательно имеем f (z) = -

åç

÷

-

å

= -

- å

ê

+

ú

n

2

2

n

z

n

2 n=0

è 2

ø

n=1

z

n=1

ë

û

Для этой функции можно получить и другие разложения в других областях. Так, например, в области z <1она аналитична и разлагается в ряд Тейлора:

1

= -

1

+

1

=

1

-

1

×

1

=

(z -1)(z - 2)

z -1

z - 2

1- z

2

z

1-

2

æ

ö

n

1

z

z

2

z

n

=1+ z + z

2

+...+ z

ç

÷

+...

-

ç1

+

+

+...+

+...÷

=

2

2

2

2

2

n

è

ø

∞ æ

1

ö n

= åç1

-

÷z

,

z

<1.

2

n+1

n=0 è

ø

Разложим ее в кольце 0 < z -1 <1 (окрестность точки z0 =1) по степеням z −1:

f (z) = -

1

+

1

= -

1

-

1

=

z -1

z - 2

z

-1

1

- (z -1)

1

∞

∞

= -

- å(z -1)n

= -å(z

-1)n , 0 <

z -1

<1.

z -1

n=0

n=−1

Таким образом, для одной и той же функции можно получить различные разложения. Это не противоречит единственности разложения, ибо полученные ряды имеют место в различных областях.

1

33. Разложить функцию

f (z) =

в ряд Лорана в кольце 0 <

z -1

<1.

z(z -1)

∞

Ответ:

f (z) = -åzn

n=−1

z − 2 функцию f (z) =

z4

34. Разложить в ряд Лорана по степеням

.

(z - 2)2

Ответ:

f (z) =

16

+

32

+ 24 + 8(z - 2) + (z - 2)2 .

(z - 2)2

z - 2

35.

Разложить

в ряд

Лорана следующие функции в указанных

областях:

а)

z

при

(z2 -1)(z2 - 4)

1<

z

< 2 , б)

1

при 1

<

z

< 2 ,

в)

1

при

z

> 2 .

(z2 -1)(z2 - 4)2

(z2 -1)(z2 - 4)2

1

∞

1

1 ∞

z2n+1

1 ∞

2n

3n + 7

Ответ: а)

å

-

å

, б)

åan z

,

an =1 при n < 0 ,

an

=

при n > 0 ,

z

2n+1

4

n

4

n+2

3 n=1

12 n=0

9 n=−∞

в)

1

å∞ [1+ (3n - 7)4n−2 ]z−2n .

9 n=1

3.Изолированные особые точки и вычеты функций

3.1.Классификация особых точек

Точки, в которых функция f (z) перестает быть аналитической, называются особыми. Если в

достаточно малой окрестности особой точки нет других особых точек, то данная особая точка на- зывается изолированной. Изолированные особые точки бывают трех типов: устранимая особая точка, полюс, существенно особая точка.

Изолированная особая точка z0 функции f (z) называется устранимой (или правильной), если существует конечный предел lim f (z) при z ® z0 (этот предел не совпадает с f (z0 ) ). Для того чтобы изолированная особая точка z0 функции f (z) была устранимой, необходимо и достаточно, чтобы лорановское разложение f (z) в окрестности z0 не содержало главной части, т.е. представляло бы ряд

Тейлора:

∞

åan (z - z0 )n = a0 + a1(z - z0 ) +...+ an (z - z0 )n +...

n=0

Данная функция совпадает с суммой ряда, если z ¹ z0 Функция будет аналитической и в точке z0 , если положить f (z0 ) = a0 , что обычно и делают.

Изолированная особая точка z0 функции f (z) называется полюсом, если lim f (z) = ¥ при z ® z0 . Для того чтобы изолированная особая точка z0 функции f (z) была полюсом, необходимо и достаточно, чтобы главная часть лорановского разложения f (z) в окрестности z0 содержала бы лишь конечное число членов:

a−m

a−m+1

a−1

∞

f (z) =

+

+...+

+ åan (z - z0 )n

(z

- z0 )

m

(z

m−1

- z0 )

z - z0

n=0

m > 0,

a−m ¹ 0 , -т называется порядком полюса, при т = 1 полюс, называется простым.

Если для

f (z) точка

z0 есть полюс порядка т, то для функции

1

точка z0 есть нуль порядка т

f (z)

(точка z0

называется нулем порядка т,

если разложение в степенной ряд аналитической функции w(z)

∞

имеет вид

w(z) = åak (z - z0 )k

, a−m ¹ 0 ,

k ³1).

k =m

Изолированная особая точка z0

функции

f (z) называется существенно особой, если lim f (z)

при

z ® z0

не существует.

1

1

Например, z

=

0 для функции

f (z) = e

z

является существенно

особой, так как lim e

z

= 0 ,

z→0−

1

lim e

z

= ¥ .

z→0+

Для того чтобы изолированная особая точка z0

функции f (z) была существенно особой, необходимо и

достаточно, чтобы главная часть лорановского разложения функции

f (z)

в окрестности z0 содержала

∞

бы бесконечное число членов:

f (z) = åan (z - z0 )n .

z = ∞ . Точка

n=−∞

Теперь о точке

z = ∞ называется бесконечно удаленной изолированной особой точкой,

если все другие особые точки находятся на конечном расстоянии от начала координат.

Точку

z = ∞ будем называть устранимой особой точкой функции

f (z) ,

если ее разложение в ряд

∞

Лорана имеет вид

f (z) = åan z−n

или существует предел

lim f (z) = a0

при

z → ∞ , т.е. функция

n=0

∞

ограничена в окрестности бесконечно удаленной точки. Пусть в разложении åan z−n будут равны нулю

n=0

a0 = a1 = ... = am−1 = 0 , но am ¹ 0 . В этом случае говорят,

что точка

z = ∞ является нулем кратности т

функции f (z) .

Точка

z = ∞ называется

полюсом

порядка m функции

f (z) , если

разложение

в ряд Лорана в

∞

окрестности этой

точки

имеет

вид

f (z) = åan z

−n ,

где

a−m ¹ 0 .

Видно,

что

в этом случае

lim f (z) = ∞ при z → ∞ .

n=−m

Бесконечно удаленная точка называется существенно особой точкой функции

f (z) , если разложение в

∞

ряд Лорана для нее имеет вид

f (z) = åan zn , причем главная часть состоит из бесконечного числа

членов.

n=−∞

36. Определить характер точки 20 для следующих функций: а) sin z + 3sin 2 z, z0

= kp, k Î Z ,

p

3 p

cos 2 z

sin z

б) sin( z -1) cos

2 z, z0 =1,

в)

, z0

=1, г)

, z0 = p.

sin 2 (z -1)

z - p

Ответ:

а) z = kπ— простые нули функции;

б) z =1— нуль четвертого порядка;

в) z =1— полюс

первого порядка; г) z = π — устранимая особая точка.

37. Определить порядки полюсов z0

для следующих функций:

а)

z

, z

0

= kp, k Î Z , б)

z2 -3z + 2

, z

0

= 2, z

0

=1

, в)

cos pz +1

, z

0

= -1, z

0

= 2 .

sin3

z

(z2 - 4)2 (z -1)3

(z2 - z - 2)3

Ответ:

а)

z = 0 — полюс второго порядка, z = kπ — полюсы 3 порядка (k = 0, ±1, ±2, . . .); б) z = 2 —

полюс 1 порядка, z =1— полюс 2 порядка, в) z = −1— простой полюс, z = 2 –полюс 3 порядка.

38. Найти особые точки функций и определить их тип (для полюсов указать порядок):

z + 2

, б) ctgz ,

1

e

1

, д) cos

1

а)

в)

,

г)

z−2i

.

z(z +1)(z -1)3

(z2 + i)3

z + i

Ответ:

а) z =1— полюс 3 порядка z = 0 и

z = −1— полюсы 1

порядка;

б)

z = kπ— простые

полюсы (k = 0,±1,±2,. . . );

в)

±

2

(i -1) —полюсы 3 порядка; г) z = 2i — существенно особая точка,

2

д) z = −i — существенно особая точка.

e

1

39. Найти особые точки функции

f (z) =

z−1

.

ez

-1

Ответ:

z =1–существенно особая точка,

z = 2kπi

(k= 0, ±1, ±2,

. . .)—полюсы 1

порядка, z = ∞ –

устранимая особая точка.