4.3. Интегрирование по частям Пусть две дифференцируемые функции изависят от. Тогда

.

интегрируя обе части равенства, получим:

или

Данная формула называется формулой интегрирования по частям и применяется тогда, когда, например, интеграл в левой части равенства вычислить сложнее, чем интеграл в правой части равенства. При интегрировании по частям важно правильно выделить функцию в подынтегральной функции. Иногда для получения результата формулу интегрирования по частям приходится применять несколько раз. Кроме того, интегрирование по частям применяется для получения уравнений, из которых можно найти искомую первообразную. Такие возможности возникают, когда подынтегральное выражение содержит произведение множителей видаsin kx или cos kx и e^nx, и в некоторых других случаях. Отметим некоторые из этих классов.

1.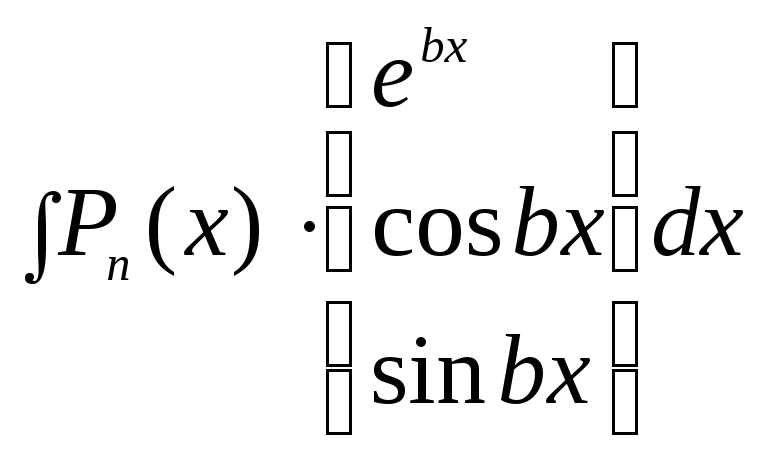, где– алгебраический многочлен степени. Данные интегралы вычисляются- кратным применением метода интегрирования по частям, последовательно полагая, затем. Получающиеся интегралы будут упрощаться, так как производная от алгебраического многочленабудет алгебраическим многочленом степени, на единицу меньшей.

2. Интегрирование выражений .

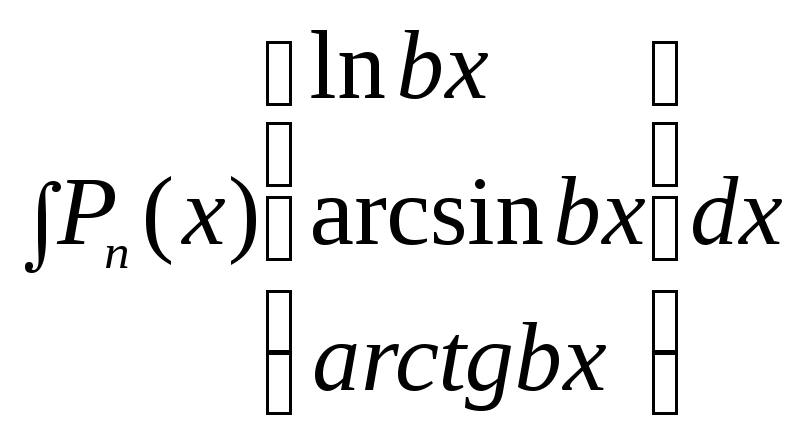Если под знаком интеграла находится произведение ал­гебраической функции (многочлен ) на логарифмическую или обратную тригонометрическую функции, то в этом случае рекомендуется за «» принимать трансцендентную функцию, а оставшуюся часть за .

3. Интегрирование выражений вида .

Если под знаком интеграла находится произведение по­казательной функции (или) на тригонометрическую( или ), то в этом случае безразлично, какую из входящихчастей подынтегрального выражения обозначать за «» или . Формула интегрирования по частям при этом применяется дваж­ды, и в правой части получается такой же интеграл, что и в ле­вой.

Типовой пример

Вычислить интеграл .

►Обозначим: , . Тогда: , . По формуле интегрирования по частям получаем:

.◄

Типовой пример

Вычислить интеграл .

►Обозначим: ,. Тогда: , . По формуле интегрирования по частям получаем:

.◄

Типовой пример

.

►Пусть ,. Тогда,и по формуле (3)

.

Для нахождения интеграла снова применим формулу (3). Положим,. Тогда,и. Окончательно получаем:

=.◄

Типовой пример

.

►

.

Тогда 2I = e^x (sin x – cos x), или ◄

§2. Интегрирование рациональных функций.

1. Интегрирование простейших дробей

Рассмотрим правильные рациональные дроби вида

, ,,,

где ,– натуральное число (). Эти дроби называютсяпростейшими I, II, III, IV типа соответственно.

1.1. Интегрирование простейших дробей I и II типа не представляет сложности. Действительно,

,

.

1.2. Для нахождения интеграла от простейшей дроби III типа преобразуем сначала ее знаменатель:

,

а затем введем новую переменную . В результате интеграл будет приведен к виду, где(подкоренное выражение будет положительно в силу условия). Получившийся интеграл можно представить в виде суммы двух интегралов, один из которых легко найти, внеся знаменатель под знак дифференциала, а другой – табличный. Действительно,

.

1.3. Рассмотрим интегрирование простейших дробей IV типа. Эта задача довольно сложная. Сначала необходимо, как и в случае простейшей дроби III типа, выделить полный квадрат в квадратном трехчлене :

,

и сделать замену . В результате получим интеграл вида

.

Его можно представить в виде суммы двух интегралов

,

первый из которых легко найти:

.

Что касается интеграла , то для его вычисления получим рекуррентную формулу (т.е. формулу, сводящую вычислениек вычислению). Преобразуем этот интеграл следующим образом:

.

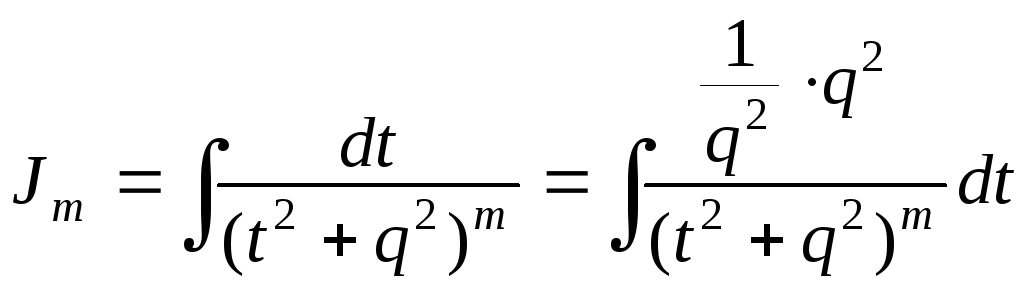
Первый их получившихся интегралов есть ; ко второму применим формулу интегрирования по частям:

,

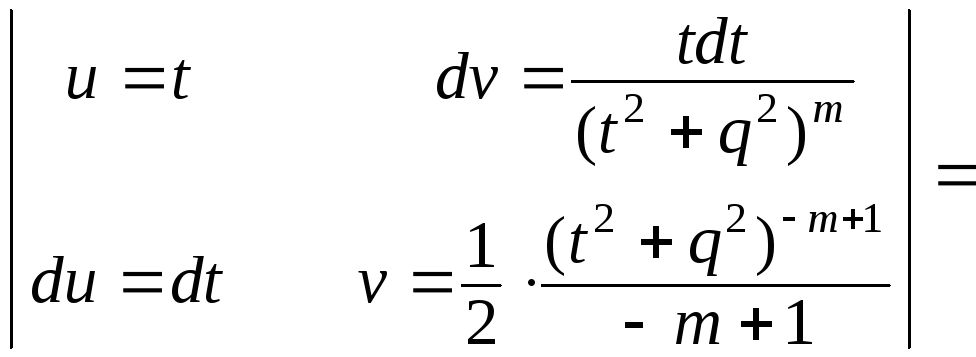
т.е. опять пришли к интегралу . Таким образом, для интеграламы получили:

,

откуда, раскрыв скобки и приведя подобные, находим

. (1)

Это и есть искомая рекуррентная формула, которая приводит к интегралу того же типа, но с меньшим на единицу показателем знаменателя. Применяя формулу (1) последовательнораз, мы сведем интегралк табличному интегралу

.

Типовой пример

Найти .

►Так как , то дробь является простейшейIII типа. Выделим полный квадрат в знаменателе:

и сделаем замену ,. Получаем

.◄

Типовой пример

Найти .

►Так как , то дробь является простейшейIV типа. Выделим полный квадрат в квадратном трехчлене:

и сделаем замену

, .

Получаем

Первый из полученных интегралов найдем, внеся функцию под знак дифференциала:

.

Для нахождения второго интеграла используем формулу (1):

.

Окончательно получаем:

.◄