Принцип перестановочной двойственности
Рассмотрим две системы:
1. Пластинка (вид с торца) с электрическим током IЭ.
2. Две заряженные полуплоскости.
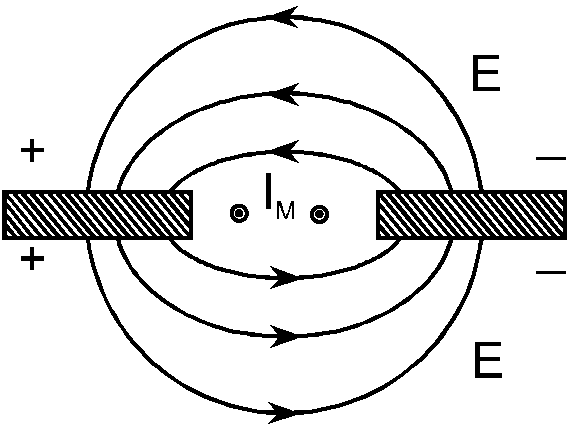
Ширина
пластинки и зазора -
.
Картинки однотипны с точностью до направлений стрелок.
Это сходство позволяет формально предположить: в щели параллельно кромкам протекает гипотетический ток IM , называемый магнитным током (физически не существует).
Геометрическое сходство полей - следствие симметрии двух основных уравнений Максвелла:
Которые
переходят одно в другое при перестановках
Если
в первом уравнении был ток jCT
Э, то следует
предположить наличие jCT
M и
.
Если найдено решение какой-либо задачи ЭД, то простая перестановка дает решение дуальной (двойственной) задачи, причем физически реализуемой.
Лемма Лоренца
Оценим связь между полями, возбужденными двумя независимыми системами сторонних токов.
Поле, созданное одной системой:
;
(1.17)
для другой
(1.18)
Проделаем ряд операций:
-
умножим скалярно первое уравнение из
(1.17) на вектор
-
умножим скалярно второе уравнение из
(1.18) на вектор
- вычтем второе равенство из первого, учитывая векторное тождество:
получим:
( ** )
Теперь
умножим второе уравнение из (1.17) на
,
а первое из (1.18) на
и вычтем второе равенство из первого,
получим:
( *** )
Складываем почленно равенства (**) и (***), получим:
(1.19)
Уравнение (1.19) - Лемма Лоренца в дифференциальной форме.
Векторные произведения [E1H2] и [E2H1] в левой части уравнения - взаимные векторы Пойнтинга двух независимых процессов.
Проинтегрируем уравнение (1.19) по произвольному объему V и используем теорему Остроградского-Гаусса, получаем Лемму Лоренца в наиболее общем виде:
где S - поверхность, ограничивающая объем V.
Предположим, что V - все пространство, т.е.(S - бесконечно большая).
Полагаем, что источники сосредоточены в конечной области пространства и, кроме того, на бесконечности поля убывают быстрее, чем 1/R, где R - расстояние от фиксированной точки. (Это физически обоснованно, т.к. в пространстве всегда будут причины для ослабления поля - потери)
Интеграл в левой части при этом становится исчезающе малым, и Лемма Лоренца для безграничного пространства, имеющего в каждой точке некоторые потери, принимает вид:
.
Упростим задачу, полагая, что в пространстве есть только сторонние электрические токи (любая проволочная антенна), тогда:
Последнее соотношение - теорема взаимности для антенн, возбуждаемых электрическими токами.
В простейшем случае если имеются две идентичные антенны, возбуждаемые одинаковым образом, то первая антенна будет создавать вблизи второй такое же поле, как вторая вблизи первой, независимо от параметров среды, разделяющей их (исключение – анизотропные среды).
В общем случае теорема взаимности связывает свойства приемной антенны со свойствами ее в режиме передачи.
В частности Диаграммы Направленности, (в дальнейшем ДН) в обоих режимах совпадают.
В анизотропных средах теорема взаимности справедлива, если:
(для ферритов - нет, для кристаллов - да).
ВОЛНЫ.
Процесс распространения колебаний в пространстве называется волной.
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они «бегут» от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.