Лианеаризация не линейных характеристик

Выбираем на данной характеристику точке А, которая будет соответствовать задающему режиму работы элемента. С достаточной степенью точности криволинейный отрезок САД заменяется прямолинейным совпадающим с касательной, проведенной в этой кривой в точке А с координатой с «Д» и считается зависимость Хвых =f (Хвх) на этом участке линейной т.е. ΔХвых = К • Хвых

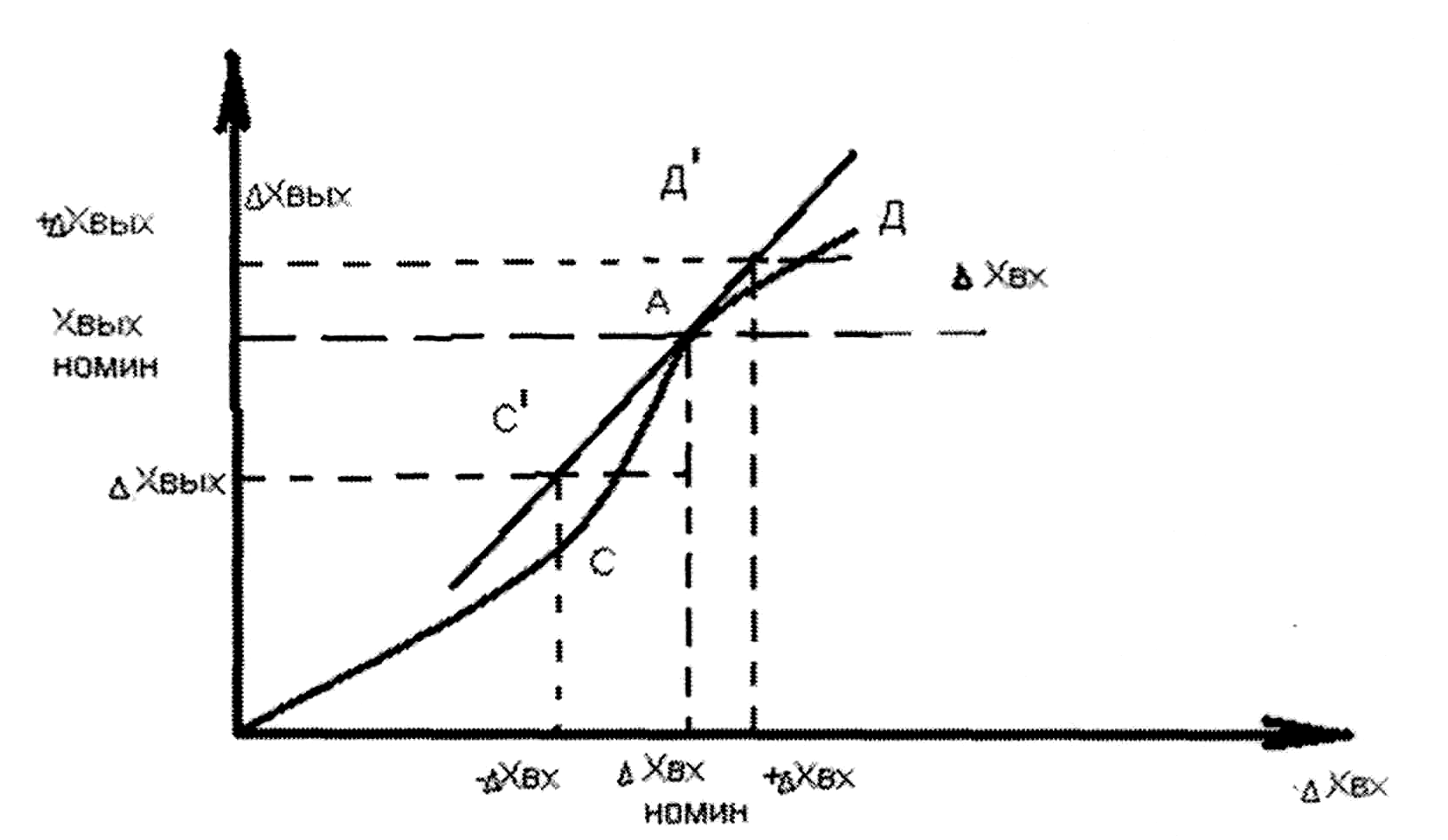
Хвых = f(Xвx), разложим в ряд Тейлора, по стечении малых отклонений в точке А:

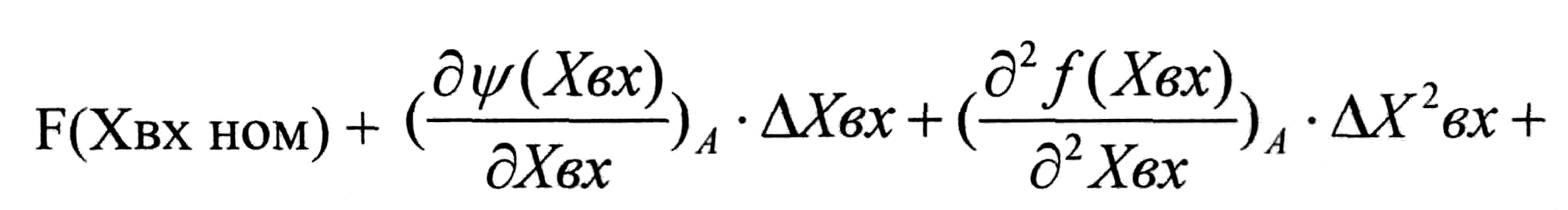
Все частные производные берут в точке А, где функция Хвх имеет const значения, по этому коэффициент при Хвх и X² вх будут постоянны. Кроме того, пренебрегают членами высшего порядка, начиная с X² вх, тогда уравнение звена запишется:

Хвых а ± ∆Хвых= Хвых а ± К * ΔХвх, где

К= ΔХвых/ΔХвх= ₍df(Xвx)/дХвх^)А

Этого и следовало ожидать, т.к. частная производная трактуется как tga касательной С"Д" в точке А, т.е. чем меньше отклонения от Хвх , тем больше линейная зависимость будет отражать истинную и чем ближе функция Хвых = Хвх к прямой, тем в больших пределах можно допустить линеаризацию. Существенное значение для анализов уравнений системы имеют начальные условия. Наиболее просто выглядит решение при 0 нулевых начальных точках, т.е. когда входная величина = 0 и все ее производные =0.

На практике начальные условия обычно не равны 0 и это усложняет их анализ. При анализе пользуются следующим приемом: принимать установившемся состоянием координатном системы в точке А = 0, т.е. учитывают величину Хвх, а ее отклонения Хвх, кроме того считают что все производные по времени от Хвых = 0.

Эту операцию производят переносом начала координат в точку А.

Математически эта операция производится вычитанием через данного выражения управления установившегося состояния.

Хвых а ± ΔХвых = Хвх а ± КΔХвх

Хвых а == Хвх± ΔХвх = ± КΔХвх

Т.е. теория автоматического регулирования оперирует только малыми отклонениями и эти отклонения связанны между собой линейными зависимостями.

Динамические характеристики элементов

/^

йХвых JL

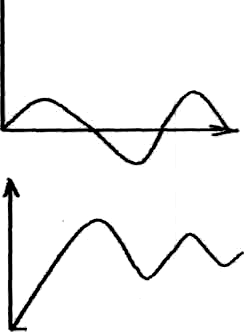
Изменения регулируемой величины во времени в результате того или иного возмущающегося воздействия вызванных этим возмущением действия регулятора называют процессом регулирования или переходным процессом (динамический режим).

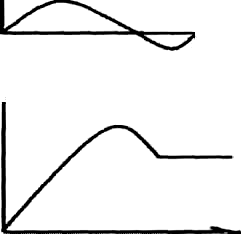
На рисунках представлены кривые переходных процессов вызванное как возмущением (А и Б, В, Г), так и изменением задания регулятору (Д и Е).

Пик выше пунктирной линии (точки задания) называется перерегулирование, на 20% выше задания (не больше).

График А - апериодически сходящиеся. Допустим, если Хмах < Хмах допустимого.

График Б - затухающий колебательный. Допустим: tp < tp допустимого.

График В - не затухающий колебательный. Допустим с малой амплитудой.

График Г расходящийся колебательный. Может быть допустим в системах автоматического регулирования (САР).

График Д - апериодически в результате управляющего воздействия.

График Е - колебательный в результате управления воздействия.

При изменении задания, отклонения отсчитывается от нового

установившегося значения, т.е. от оси абсцисс переносится в другую точку.

Если система в результате управляющего воздействия приходит к

равновесному состоянию, то она называется устойчивой (А, Б - графики).

В случае если регулируемая величина либо удаляется от значения заданного, либо совершает не затухающих колебаний - система не устойчива.

К САР представляются следующие требования:

1. Устойчивость;

2. Качество переходного процесса (минимальная статическая ошибка, minXmax, min tp)

Чем качественней система, тем она сложнее в реализации, поэтому при расчетах идут на компромисс между стремлением получить наиболее высокое качество регулирования и достичь решения задачи, возможно более простыми техническими средствами

Динамические свойства линейных элементов, а так же САР, часто описываются неоднородными, линейными, дифференциальными уравнениями.

Общий вид этих НЛДУ:

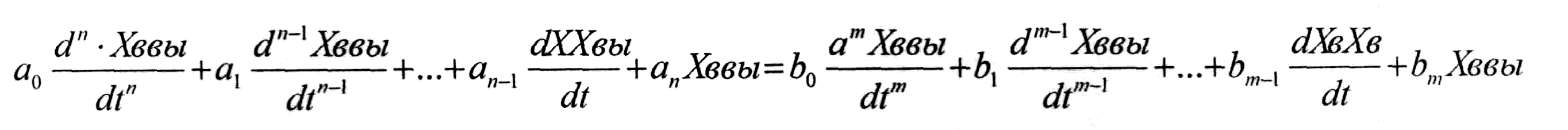
Динамические свойства не линейных элементов и систем описываются

дифференциальными уравнениями в частных производных и таких

уравнений представляющих еще большие трудности.

Поскольку большинство звеньев практически не линейные, для анализа их динамических свойств пользуются некоторыми искусственными приемами, заключающимися в следующем:

1. Не линейную характеристику; если это возможно подвергает линеаризации, т.е. криволинейный участок характеристики заменяют прямым.

2. Пользуясь преобразованием Лапласа сводят решение системы в сложным дифференциальных уравнений к системе алгебраических уравнений, решение которых не представляет трудностей.