Глава 2. Физические задачи приводящие к понятию ряда фурье

Понятие о ряде Фурье можно ввести, исходя из задачи раскладывания периодических прямоугольных и пилообразных импульсов напряжения, подаваемых на осциллограф. Следует сообщить студентам, что такие периодические сигналы могут, например, играть роль тестовых при исследовании конструкции различных частотных фильтров, «обрезающих» определенные частоты, а само разложение в ряд Фурье широко используется в радиотехнике и теории связи. Периодические прямоугольные импульсы получают при разложении в ряд Фурье функций 1) , ; 2) , , а пилообразные – раскладывая функцию , где – время. πСоответствующие коэффициенты и находят по методу Эйлера-Фурье в предположении, что разложение имеет место.

1)Разложить функцию

в промежутке (-π, π).

По формулам:

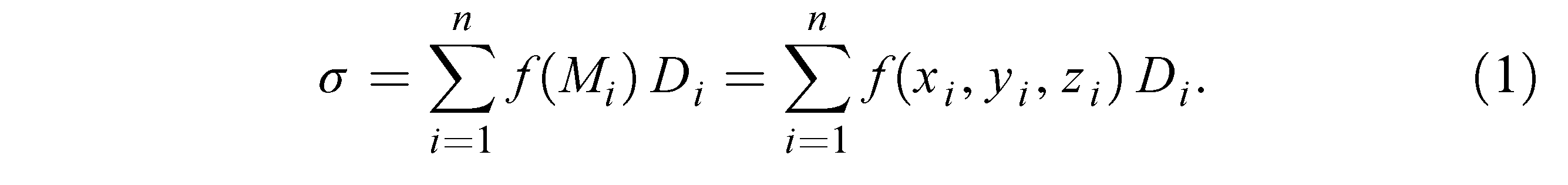
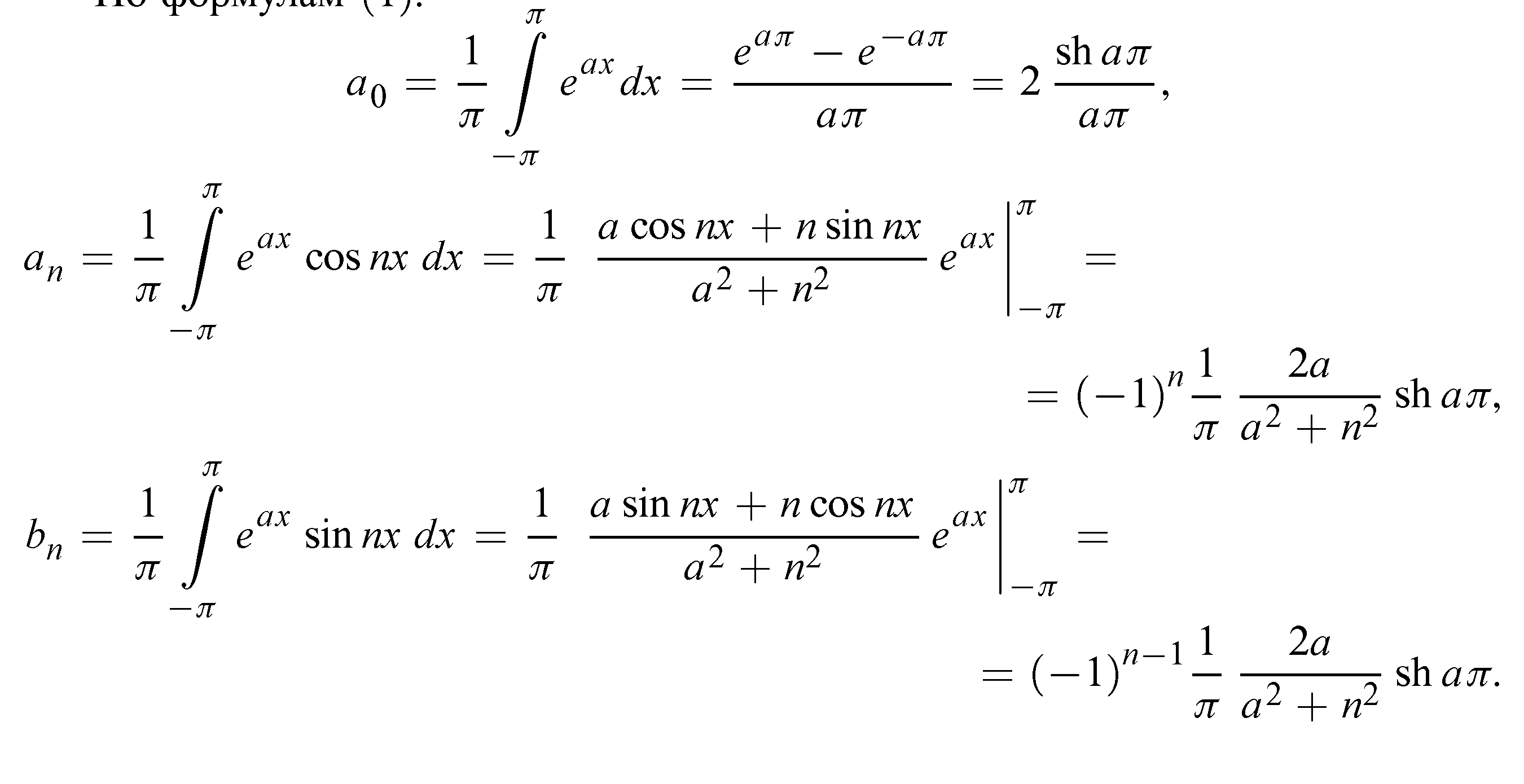
Итак, для –π<x< π будем иметь

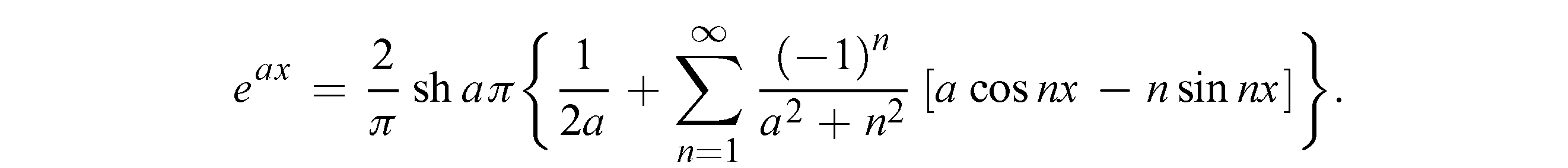
2)Разложить функцию

в промежутке (0, 2π)

Поформулам:

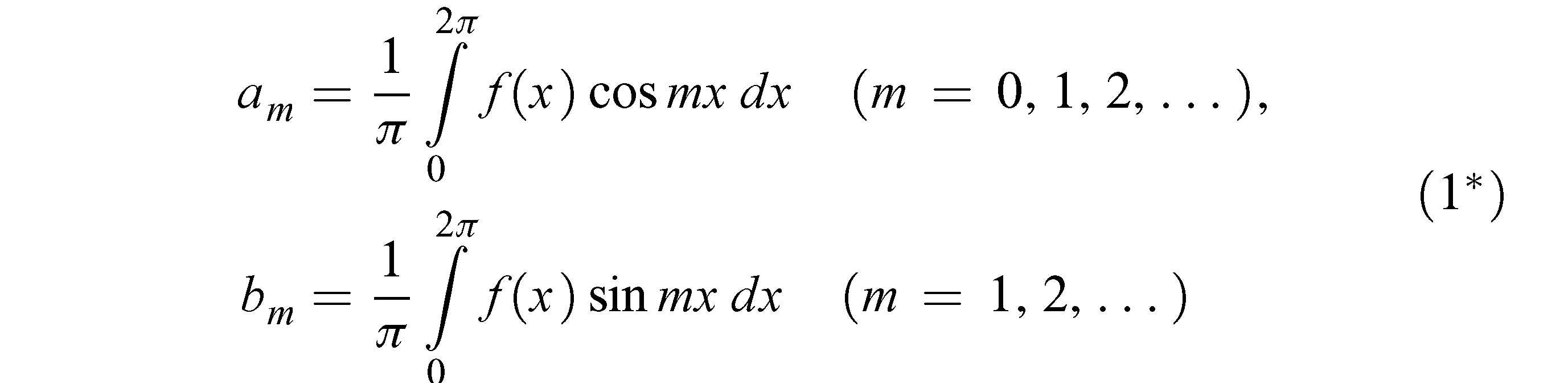
получим

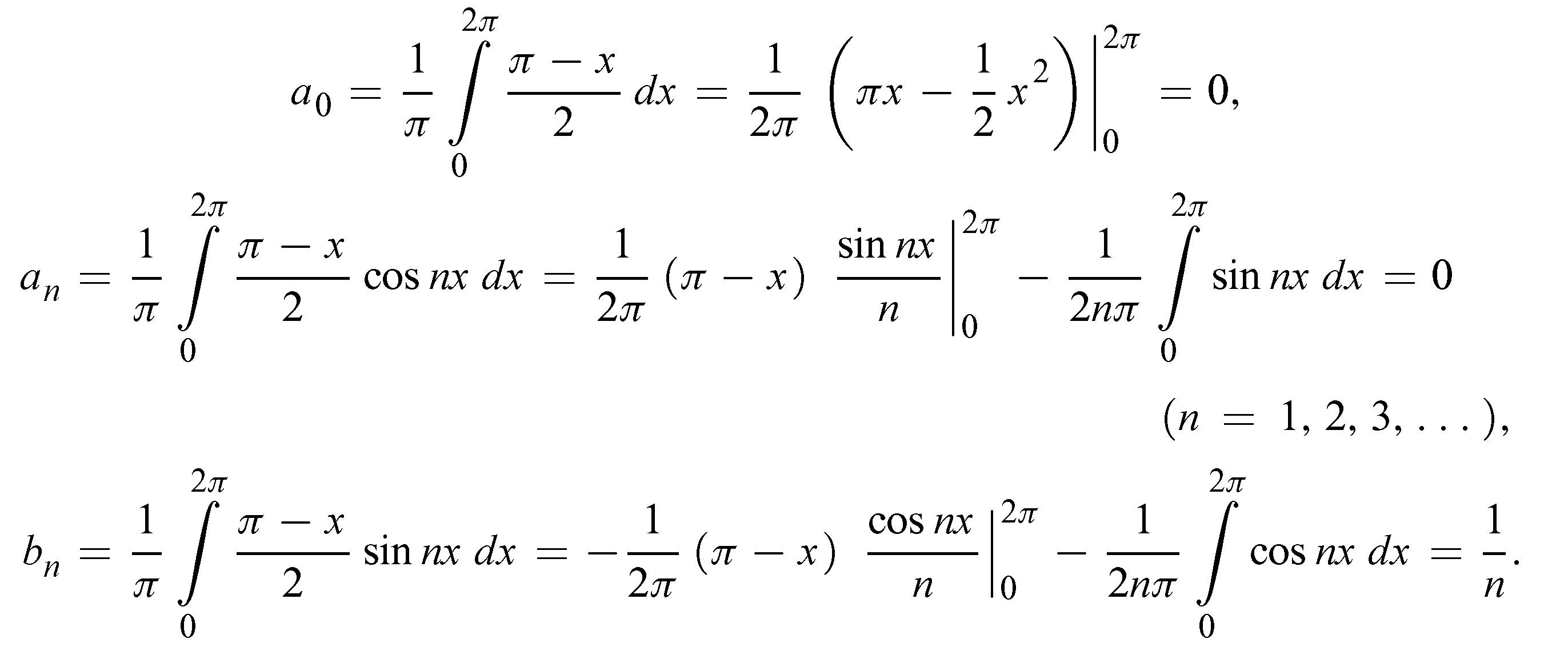
Таким образом, мы приходим к замечательному по простоте разложению, содержащему одни лишь синусы:

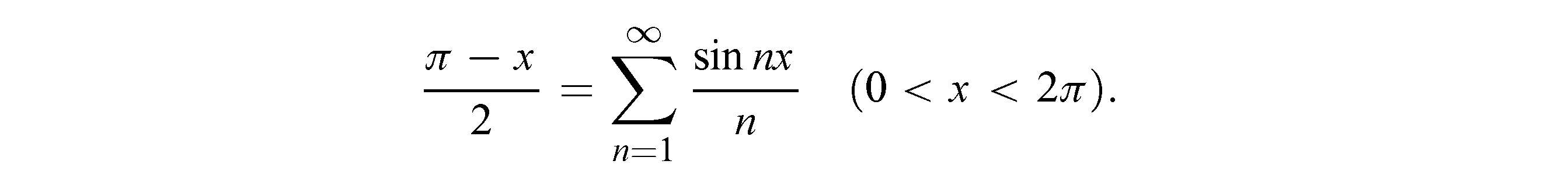
При x=0 (или 2π) сумма ряда равна нулю, и равенство нарушается. Не будет равенства и вне указанного промежутка. График суммы ряда S(x) (рис.124) состоит из бесчисленного множества параллельных отрезков и ряда отдельных точек на оси х.

U

t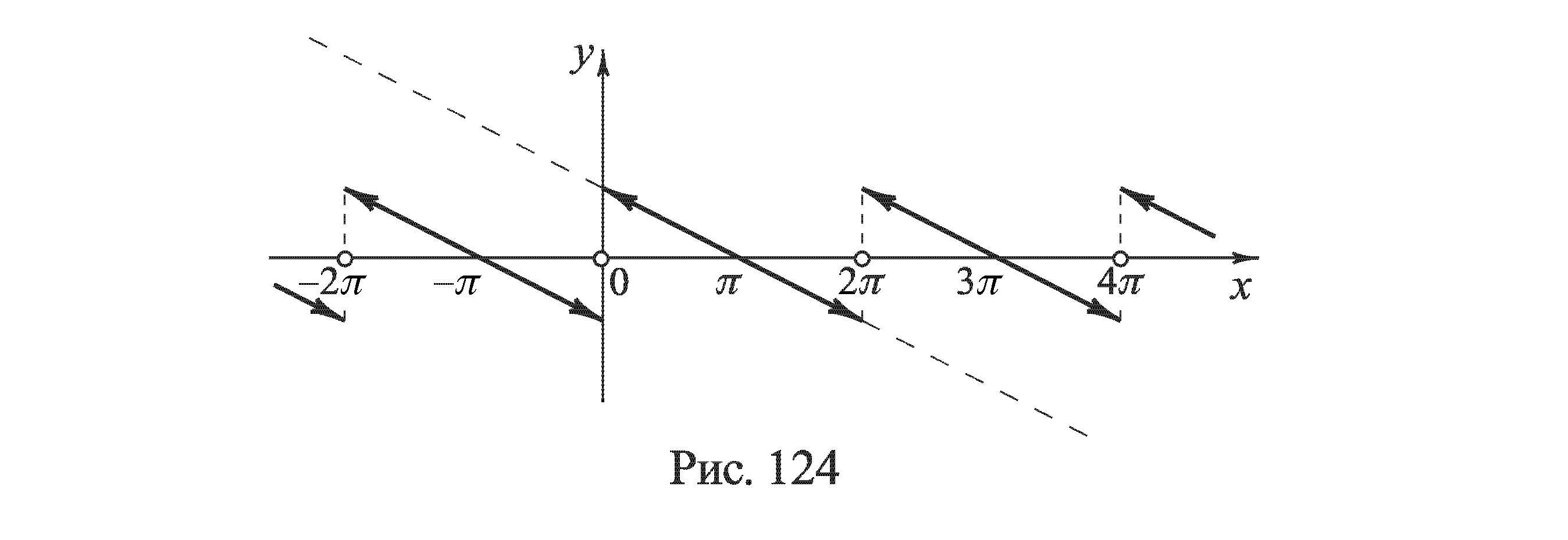

3)Ввиду особой важности разложения, полученного в предыдущем упражнении, мы дадим элементарный вывод его, не опирающийся на общую теорию.

Пусть 0<x<2π. Воспользовавшись формулой (26)

Которую мы можем написать так:

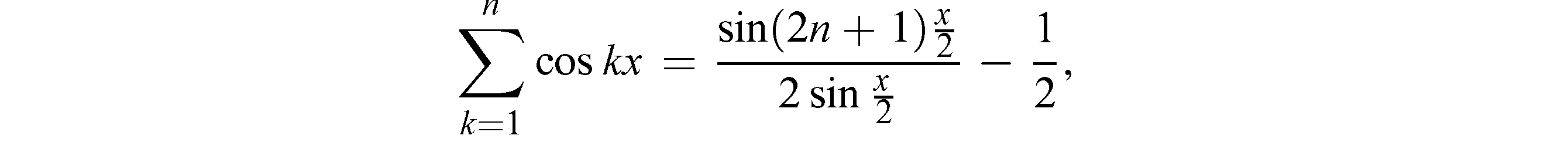
Имеем последовательно:

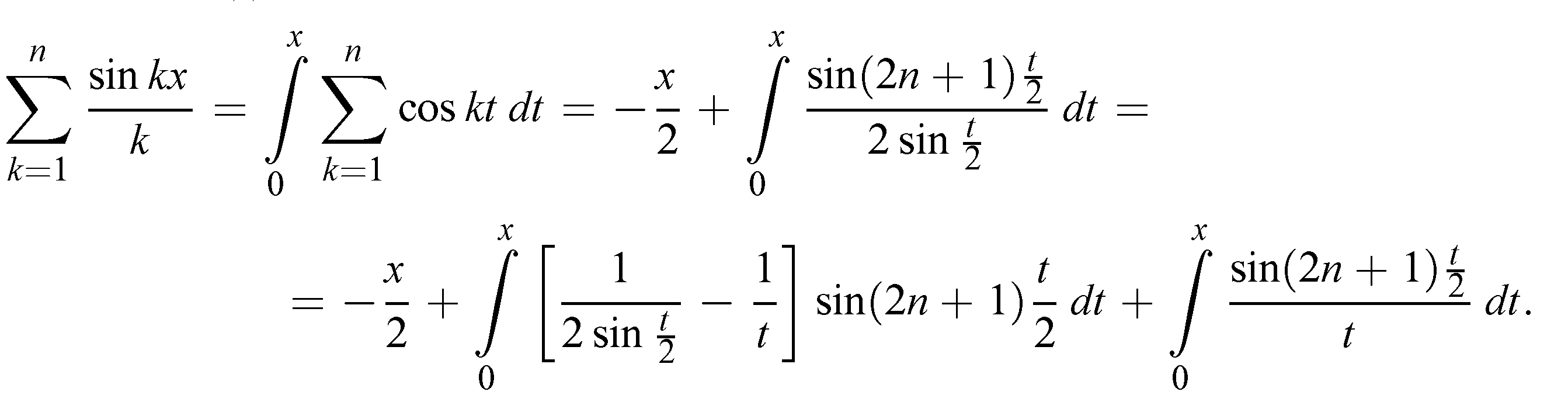
Но приn→+∞ второй член в последовательней части равенства стремиться к 0 по основной лемме, а третий член подстановкой u=(2n+1)t/2 преобразуется к виду

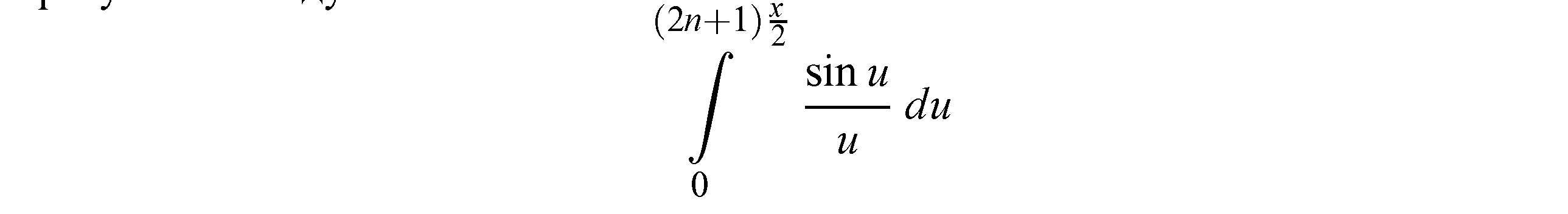
И, очевидно, стремится к

отсюда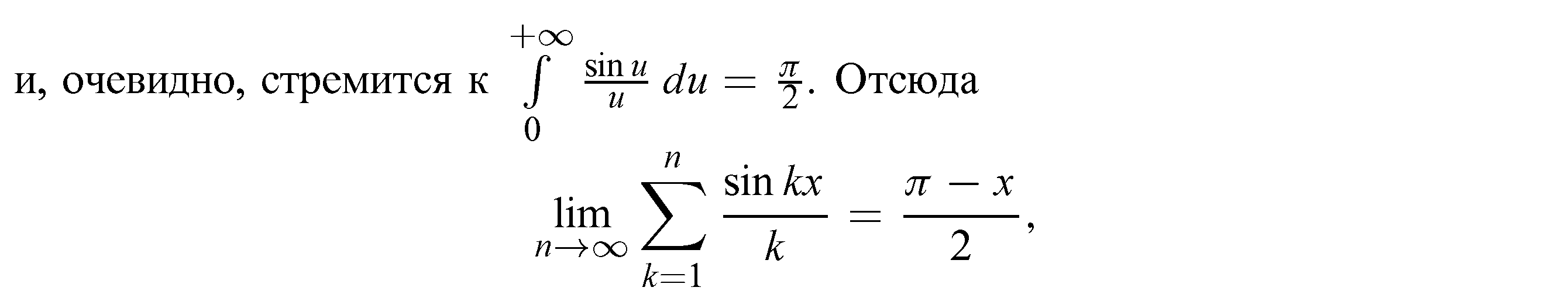

Что и требовалось доказать.

4)Из разложения в 2) уже без вычислений можно получить и другие интересные разложения. Заменяя в нем x на 2x и деля обе части равенства на 2, найдем:

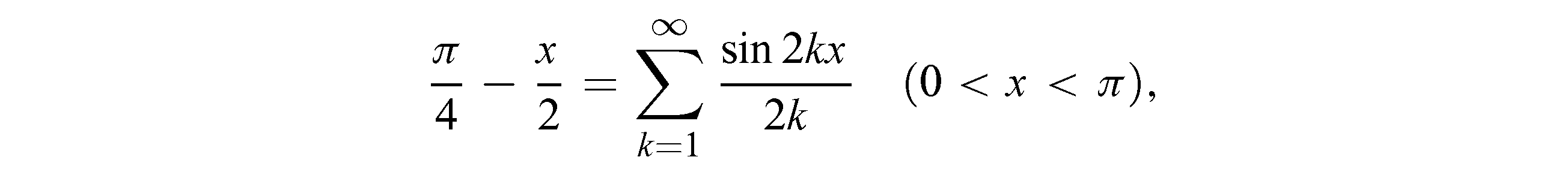
Вычитая одно и тоже разложение из другого, получим:

Если через S(x) обозначить сумму последнего ряда, то S(0)=S(π)=0. Изменяя знак x, для промежутка (-π,0) понечетности синуса найдем, что S(x)= - π/4; для прочих же значений x сумма S(x) поулчается по закону периодичности, так что, в частности, для промежутка (2 π,3 π) снова S(x)= π/4 и т.д. График функции S(x) изображен на рис. 125; а рис 126 характеризует постепенное приближение к этой разрывной функции частичных сумм ряда.

U

t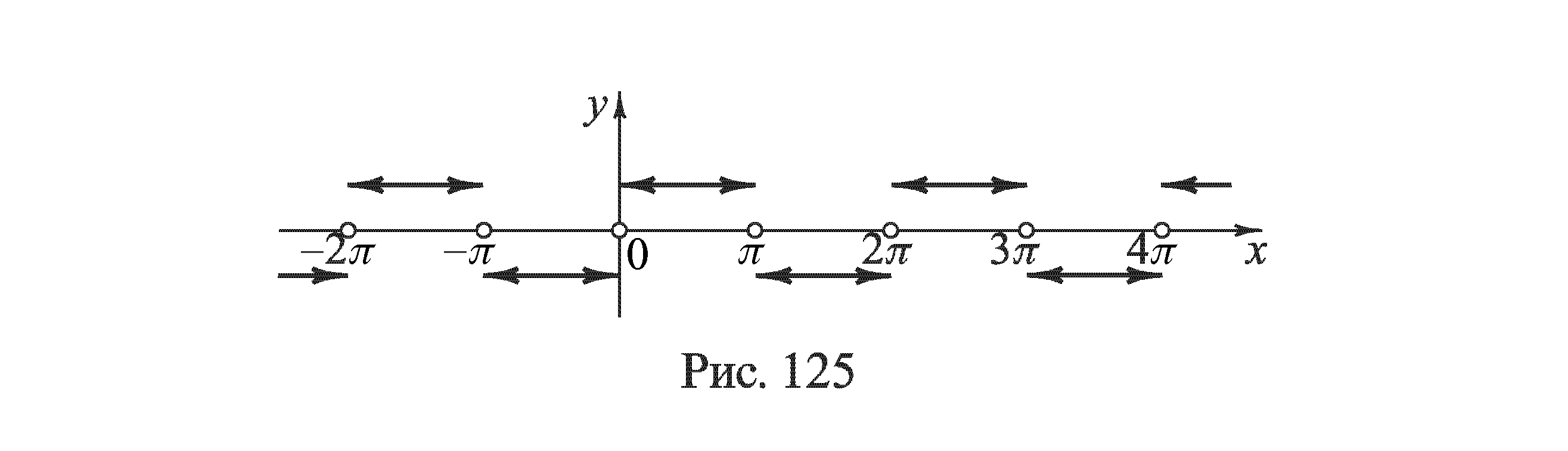

U

t

U

t

U

t

U

t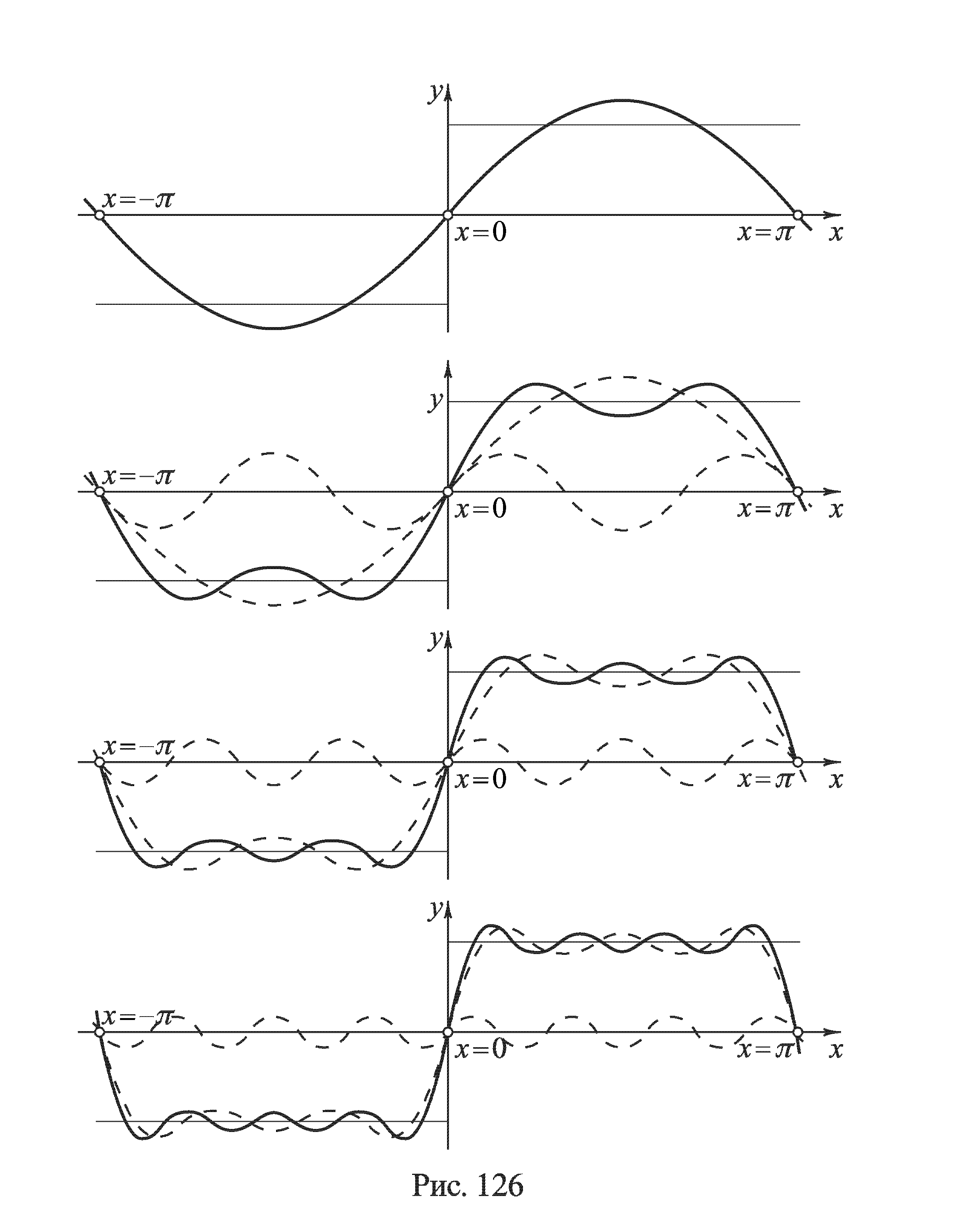

Если положить в рассматриваемом разложении x=π/2, то получим известный нам ряд Лейбница

При x=π/6 и x=π/3 получаются ряды:

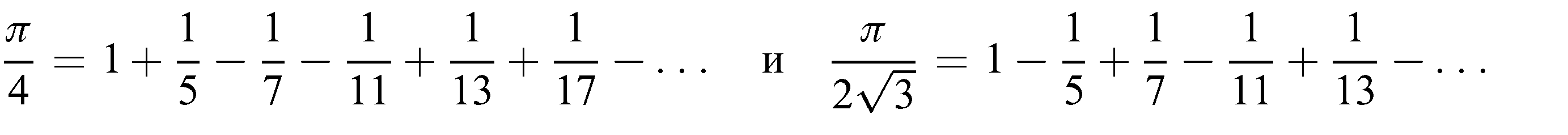
Сочетая полученное здесь разложение с разложением в 2), легко прийти к ряду для функции F(x)=x:

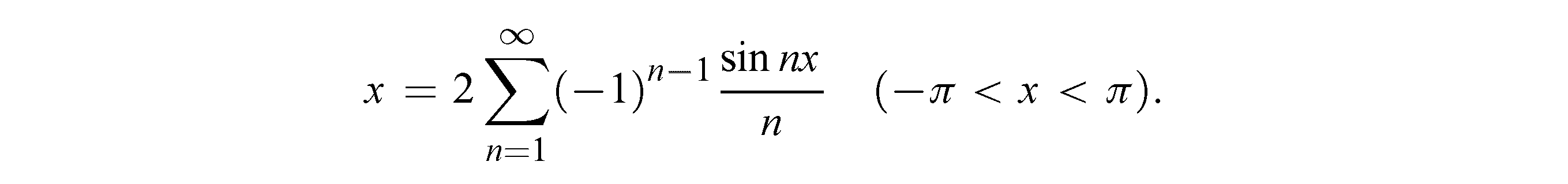
Непосредственно мы получаем его лишь для 0<x<π, но равенство явно имеет место для x=0 и, кроме того, обе его части, очевидно,представляют нечетные функции, так что окончательно разложение оказывается верным для

U

t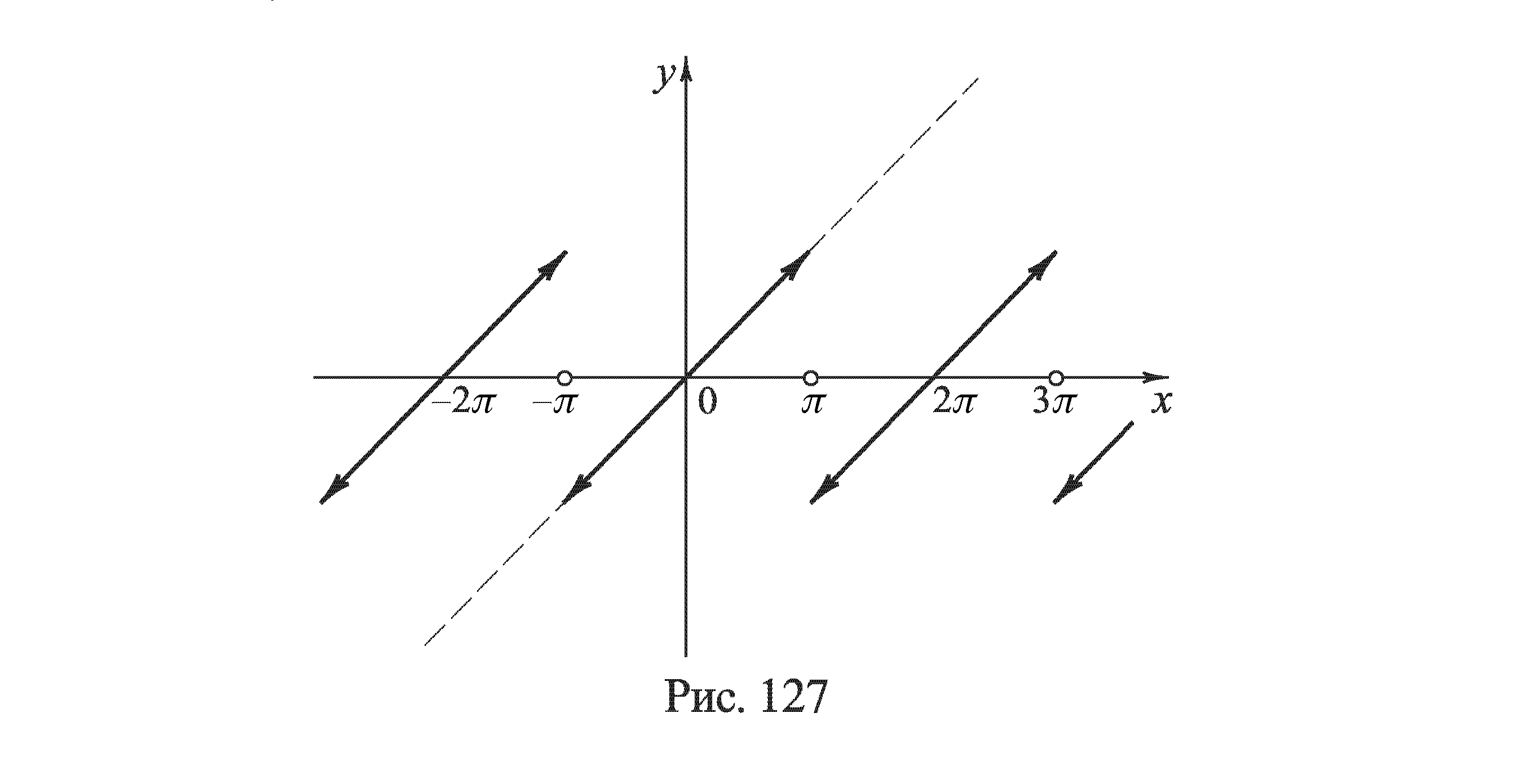

Всего промежутка (-π,π).График суммы ряда при изменении x от -∞ до +∞ легко себе представить по рис. 127. На рисунке 128 изображен график частичной суммы,а рисунки 129-131 характеризуют постепенное приближение к этой разрывной функции частичных сумм ряда

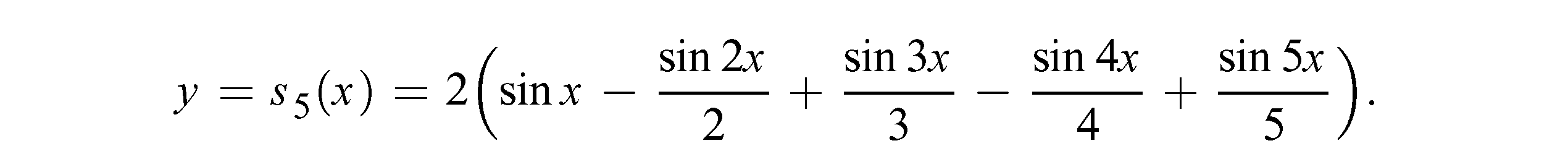
U

t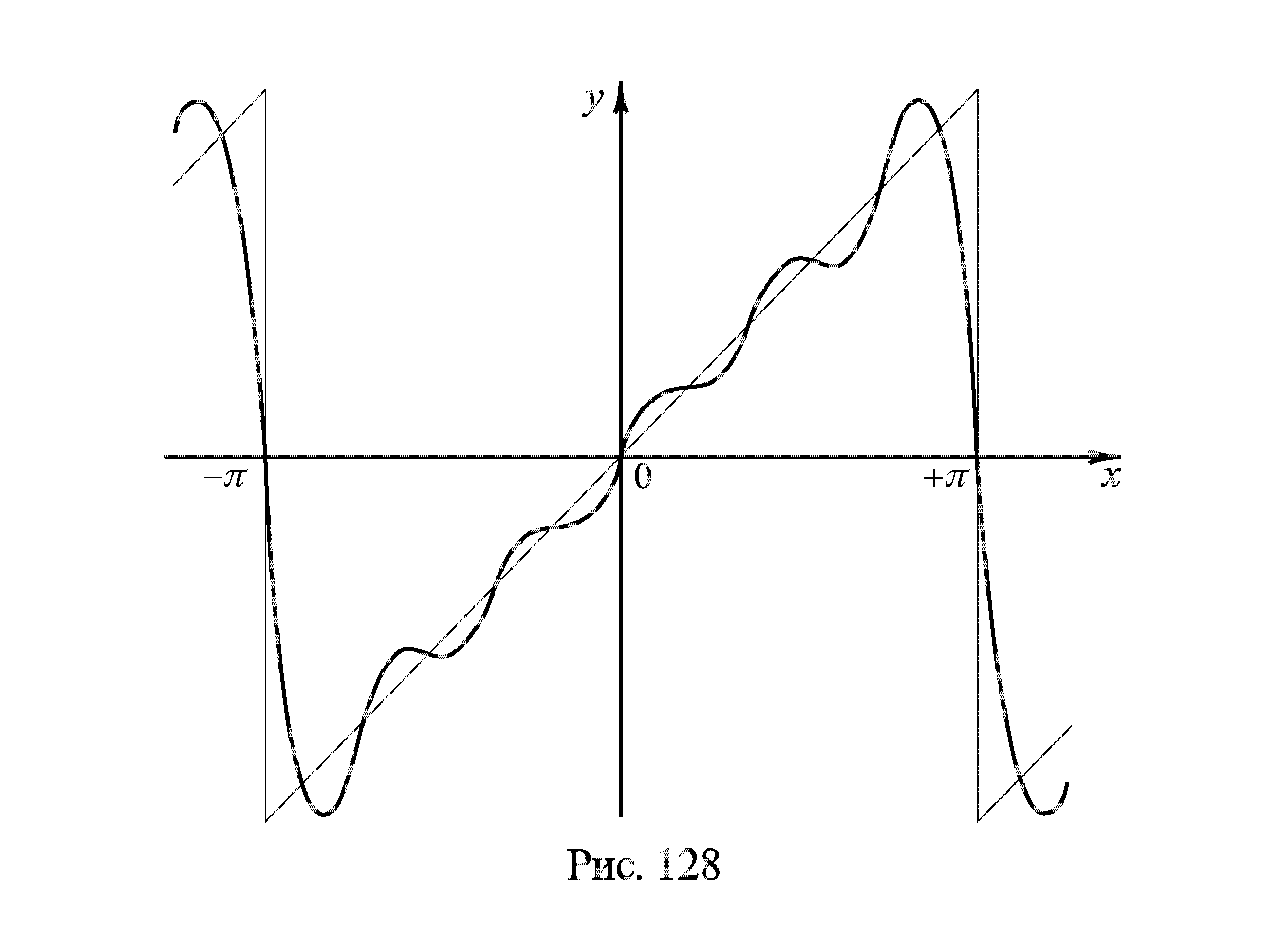

Рисунок 129

Рисунок 130

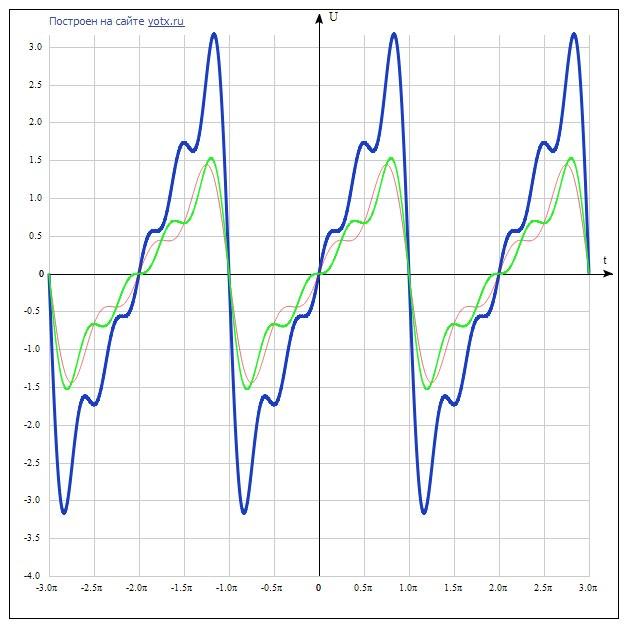
Рисунок 131

На основании рассмотренных выше примером можно сделать вывод о том, что, на самом деле, представлячет из себя определение понятия ряда Фурье.

Пусть задана функция f(x) периода 2l и известно, что ее можно разложить в тригонометрический ряд:

т. e. она уже есть сумма некоторого тригонометрического ряда вида (1) для всех t (или, быть может, для всех t, за исключением отдельных значений t). Спрашивается, как определить по функции f(t) коэффициенты a_k,b_k Этот воп­рос принципиально был решен математиками и физиками в начале прошлого столетия. Существенный вклад в его реше­ние внес Ж. Фурье. Он показал, что коэффициенты a_k,b_k тригонометрического ряда, представляющего периодическую периода 2l функцию f(t), вычисляются по формулам

Числа a_k и b_k вычисляемые по этим формулам, назы­вают коэффициентами Фурье функции f(t), а тригономет­рический ряд (1), в который вместо a_k и b_k подставлены соответствующие коэффициенты Фурье, называют рядом Фурье функции f(t).