- •1.Линейные операции над векторами
- •2. Базис и аффинные координаты. Проекция вектора на ось. Прямоугольная система координат
- •3.Деление отрезка в данном отношении. Пусть точка c лежит на отрезке ab. Говорим, что c делит отрезок ab в отношении 1:2 , если
- •3. Скалярное произведение векторов
- •2. Свойства скалярного произведения двух векторов.
- •4. Векторное произведение векторов
- •5. Смешанное произведение векторов
- •3. Свойства смешанного произведения.
- •6, Полярная система координат
- •7. Сферическая и цилиндрическая системы координат
6, Полярная система координат
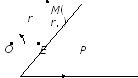
Выберем на плоскости произвольные точку O и ось OP, которая задается единичным направленным отрезком OE;\s\up10( – . Пусть M – произвольная точка плоскости. Обозначим r = OM, = (OE;\s\up10( –, OM;\s\up10( –) – ориентированный угол. Тогда пара (r, ) называется полярными координатами точки M.
Точка O называется полюсом, а OP – полярной осью. Совокупность точки O и оси OP называется полярной системой координат на плоскости.
Очевидно, что 0 r < + , а для угла обычно договариваются, что 0 < 2, либо, что – < . При этом, если r = 0, то считается неопределенным.
Выберем декартову СК так, чтобы точка O была ее началом, а положительное направление оси Ox совпадало с направлением оси OP. Пусть M1 и M2 – проекции точки M на координатные оси Ox и Oy соответственно. Тогда из OMM1 и OMM2 получаем
 x
=
r
cos
, r
=
,
x
=
r
cos
, r
=
,
y = r sin . (14) = arctg .
Вообще, знание синуса, косинуса, или тангенса в отдельности не позволяет однозначно определить угол . Его следует находить сразу из двух равенств: cos = x/r, sin = y/r,
либо так: = arccos , если y 0;
= – arccos , если y < 0 (предполагается, что – < ). Использование арктангенса неудобно: надо оговаривать еще случай x = 0 и поэтому приходится писать 4 равенства.
7. Сферическая и цилиндрическая системы координат
 Пусть
в пространстве задана декартова СК
Oxyz
и пусть M(x,
y,
z)
– произвольная точка. Опустим перпендикуляр
MMo
на плоскость Oxy.
Тогда, очевидно,
MMo=
z.
Обозначим
=OM,
=
MoOM
; при этом,
если z
>0, то
считаем, что
>0, а если
z
<0, то
<0.
Пусть
в пространстве задана декартова СК
Oxyz
и пусть M(x,
y,
z)
– произвольная точка. Опустим перпендикуляр
MMo
на плоскость Oxy.
Тогда, очевидно,
MMo=
z.
Обозначим
=OM,
=
MoOM
; при этом,
если z
>0, то
считаем, что
>0, а если
z
<0, то
<0.
Пусть (r, ) – полярные
координаты точки Mo на
плоскости. Тогда тройка (r, , ) называется сферическими координатами точки M, а тройка (r, , z) – ее цилиндрическими координатами. Очевидно, что 0 < +, –/2 /2 . Если = /2, то точка M лежит на оси Oz, Mo= O и тогда считается неопределенным.
Найдем формулы, которые связывают декартовы, сферические и цилиндрические координаты
точки M. Из OMMo находим, что
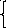
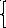 r
=
cos
,
=
,
r
=
cos
,
=
,
z = sin . = arcsin
Эти формулы можно рассматривать, как переход от сферических координат к цилиндрическим и обратно; а у этих систем координат общее. Формулы перехода от декартовых координат к сферическим:
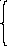
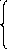 x
=
cos
cos
,
= ,
x
=
cos
cos
,
= ,
y = sin cos , = arccos ,
z = sin . = arcsin( z /) .
Во второй формуле знак выбирается в соответствии со знаком y.
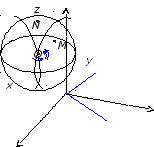
 Сферические
координаты можно использовать для
введения внутренних координат на сфере.
Если начало координат поместить в центр
сферы радиуса ,
то
и
будут играть роль географических
долготы и широты точки M,
лежащей на сфере; пишем M(,
).
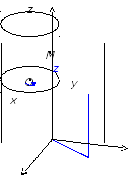
Точно также цилиндрические координаты
позволяют ввести внутренние координаты
на поверхности цилиндра. Если начало
координат разместить на оси цилиндра
радиуса r,
то
и z
будут
координатами точки
M,
лежащей
на поверхности
цилиндра; пишем M(,
z).
Сферические
координаты можно использовать для
введения внутренних координат на сфере.
Если начало координат поместить в центр
сферы радиуса ,
то
и
будут играть роль географических
долготы и широты точки M,
лежащей на сфере; пишем M(,
).
Точно также цилиндрические координаты
позволяют ввести внутренние координаты
на поверхности цилиндра. Если начало
координат разместить на оси цилиндра
радиуса r,
то
и z
будут
координатами точки
M,
лежащей
на поверхности
цилиндра; пишем M(,
z).