Тема 2.2. Функциональные (степенные) ряды 1. Степенные ряды. Основные определения.

2. Теорема Абеля об области сходимости степенных рядов. Интервал сходимости степенного ряда.

3. Свойства степенных рядов.

4. Разложение элементарных функций в степенные ряды.

5. Примеры разложения элементарных функций в степенные ряды.

Конспект лекции

1. Степенные ряды. Основные определения.

Ряд вида

(1)

называется степенным рядом.

Числа называются коэффициентами степенного ряда.

Придавая различные числовые значения, будем получать раз­личные числовые ряды, которые могут оказаться сходящимися или расходящимися Множество тех значений , при которых ряд (1) сходится, называется областью его сходимости. Это множество всегда не пусто, так как любой степенной ряд сходится при .

Очевидно, что частичная сумма степенного ряда является функцией переменной . Поэтому и сумма ряда также является некоторой функцией переменной , определенной в области сходимости ряда: (или ).

2. Интервал сходимости степенного ряда. Теорема Абеля об области сходимости степенных рядов.

Докажем теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда

Теорема 1 (теорема Абеля)

1) Если степен­ной ряд (1) сходится при , то он сходится, и при­том абсолютно, для всех , удовлетворяющих условию ;

2) Если ряд (1) расходится при , то он расходится для всех , удовлетворяющих условию .

Доказательство. 1) Так как по условию числовой ряд сходится, то его общий член при , откуда следует, что последовательность ограничена, т.е. существует число такое, что

(2)

Перепишем ряд (1) в виде

(3)

и рассмотрим ряд, составленный из абсолютных величин его чле­нов

(4)

Члены ряда (4) в силу неравенства (2) меньше соответствующих членов ряда

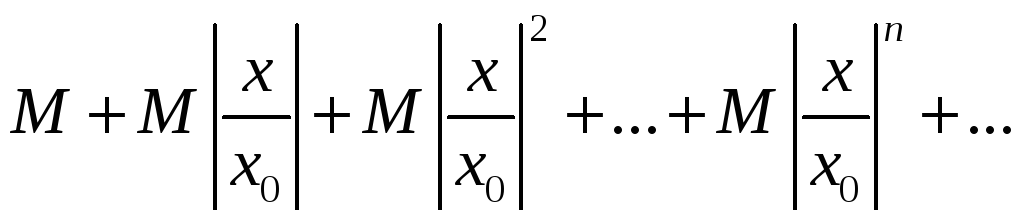(5)

при ряд (5) представляет собой геометрическую прогрессию со знаменателем и, следовательно, сходится.

Так как члены ряда (4) меньше соответствующих членов ряда (5), то, по признаку сравнения, ряд (4) также сходится, а это зна­чит, что ряд (1) при сходится абсолютно.

2) Докажем теперь вторую часть теоремы. По условию, в точ­ке ряд (1) расходится. Требуется показать, что он расходится для всех , удовлетворяющих условию . Предполо­жим обратное, т. е. допустим, что при некотором значении та­ком, что , ряд (1) сходится. Тогда по только что дока­занной первой части теоремы ряд (1) должен сходиться и в точке , так как . Но это противоречит тому, что в точке ряд

расходится. Теорема доказана.

Теорема Абеля утверждает,

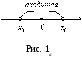
а) что если — точка сходимости степенного ряда, то во всех точ­ках, расположенных на интервале (рис. 1 а), этот ряд сходится абсолютно,

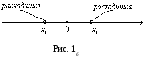
б) если — точка расходимости степенного ряда, то во всех точках, рас­положенных вне интервала (рис. 1 _б), ряд рас­ходится.

Отсюда вытекает следующая теорема.

Теорема 2. Если, ряд сходится не при всех значениях и не

только при , то существует число такое, что ряд абсолютно сходится при и расходится при .

Доказательство. Обозначим через множество то­чек , в которых ряд сходится. Покажем, что множество ограничено. Действительно, если взять точку , в которой ряд расходится (по условию такие точки существуют), то по теореме Абеля для любого из выполняется неравенство .

Известно, что у ограниченного сверху множества существует точ­ная верхняя грань. Положим . Так как ряд сходится не только при , то .

Возьмем теперь любое , для которого . Согласно свойству точной верхней грани найдется такое, что , откуда по теореме Абеля следует абсолютная сходи­мость ряда при взятом .

Возьмем теперь любое , для которого . Такое . Следовательно, при этом ряд расходится. Теорема доказана.

Таким образом, решен вопрос об области сходимости степен­ного ряда. Интервал называется интервалом сходимости степенного ряда. Число называется радиусом сходимости сте­пенного ряда.

Так как члены ряда (4) меньше соответствующих членов ряда (5), то, по признаку сравнения, ряд (4) также сходится, а это зна­чит, что ряд (1) при сходится абсолютно.

Таким образом, решен вопрос об области сходимости степен­ного ряда. Интервал называется интервалом сходимости степенного ряда. Число называется радиусом сходимости сте­пенного ряда.

Отметим, что интервал сходимости некоторых рядов охваты­вает всю числовую прямую (в этом случае пишут ) у дру­гих вырождается в одну точку ().

Итак, всякий степенной ряд имеет свой радиус сходимости

.

При ряд может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.

Приведем способ определения радиуса сходимости степенного ряда.

Теорема 3. Если существует предел 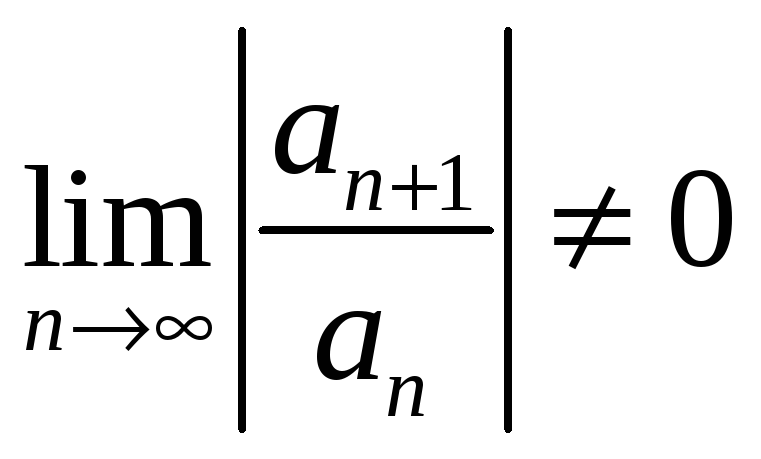, то радиус сходимости ряда равен .

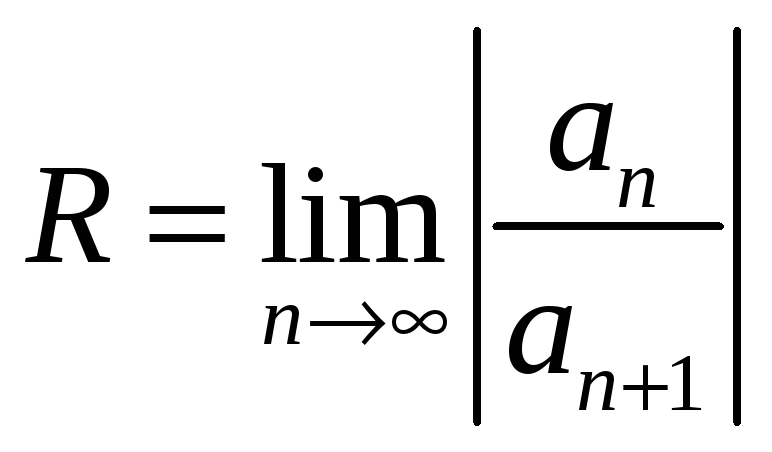Доказательство. Рассмотрим ряд . По условию существует 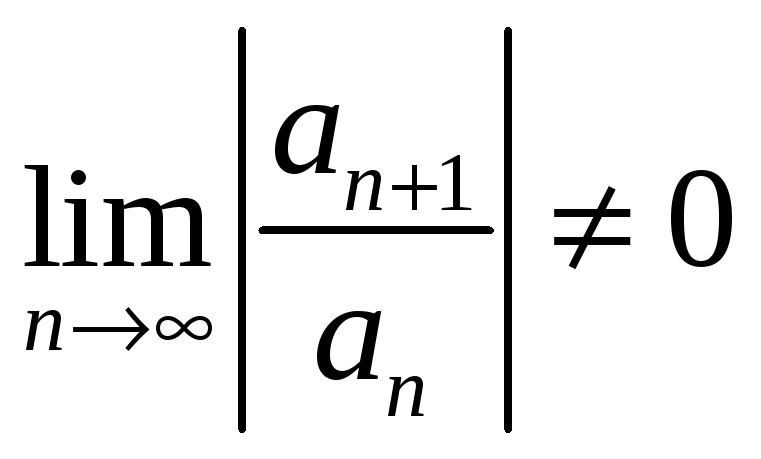. Обозначим его через . Тогда .

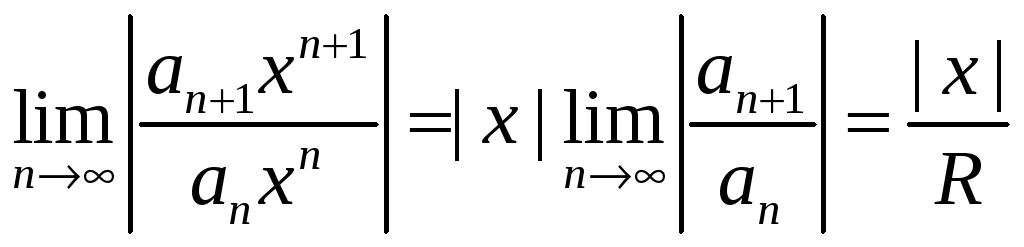При каждом значении степенной ряд становится числовым. Поэтому по признаку Даламбера ряд

сходится, если , т.е. .

Следовательно, по теореме 14.10 о сходимости знакопеременных рядов ряд также сходится при , причем абсолютно. При ряд расходится, так как 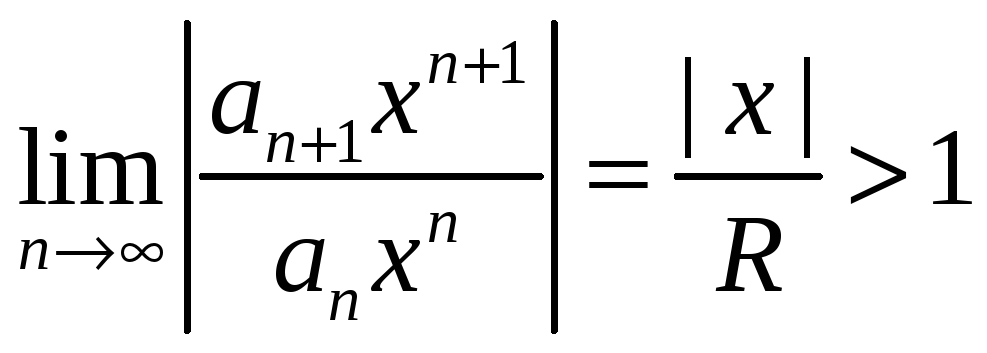и, следовательно, общий член ряда не стремится к нулю при .

Таким образом, данный ряд сходится внутри интервала и расходится вне его, т.е. радиус сходимости равен 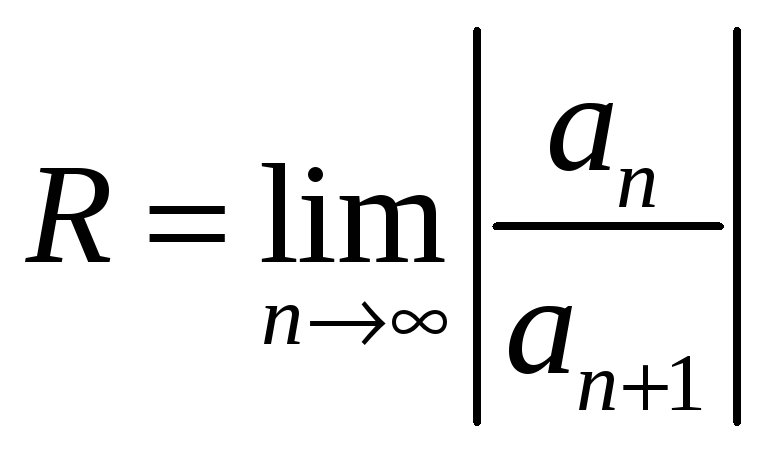. Теорема доказана.

Замечание. Можно доказать, что если 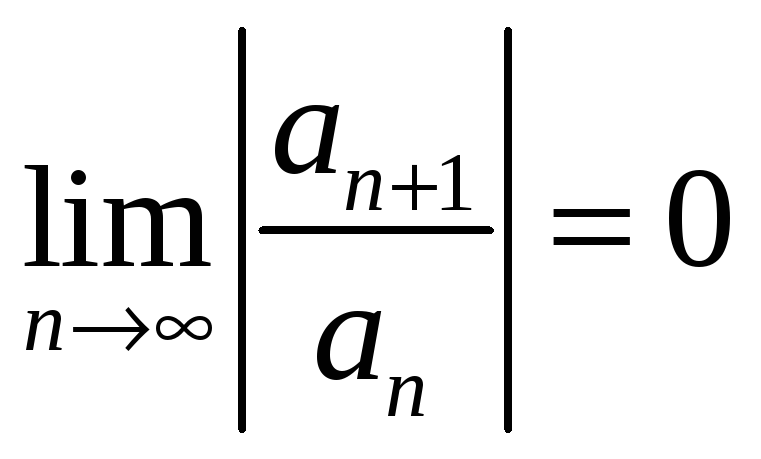, то ряд сходится на всей числовой прямой, т.е. , а если , то ряд сходится только при , т.е. .

Пример 1. Рассмотрим ряд . Здесь и . Поэтому

.

Следовательно, по теореме 14.13 данный ряд сходится на интер­вале (—1, 1). Исследуем поведение ряда на концах интервала схо­димости, т. е. в точках . При получаем гармонический ряд , а при ряд , который сходится

в силу признака Лейбница. Таким образом, данный ряд сходится в любой точке полуинтервала [— 1, 1) и расходится вне его.

Пример 2. Ряд расходится на всей числовой прямой, кроме точки ,

так как его радиус сходимости

.

Пример 3. Ряд сходится абсолютно на всей числовой прямой, так как его радиус сходимости

.