9. Теорема Кронекера-Капелли о разрешимости системы линейных алгебраических уравнений.

Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA^*.

Очевидно, что система может быть записана в виде:

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А А^* не изменяют ранга.

2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, т.е. верна запись, приведенная выше.

10. Запись и решение системы линейных алгебраических уравнений в линейном виде.

Неизвестные или переменные уравнений общепринято обозначать буквами х₁, х₂,… х_n. Уравнение называется линейным относительно переменных х₁, х₂,… х_n, если оно записано в виде .

Здесь – произвольные действительные числа.

Набор чисел называется решением уравнения, если в результате подстановки этих чисел вместо неизвестных уравнение превращается в алгебраическое тождество

.

Пусть задана совокупность уравнений. В общем виде такая система уравнений записывается так:

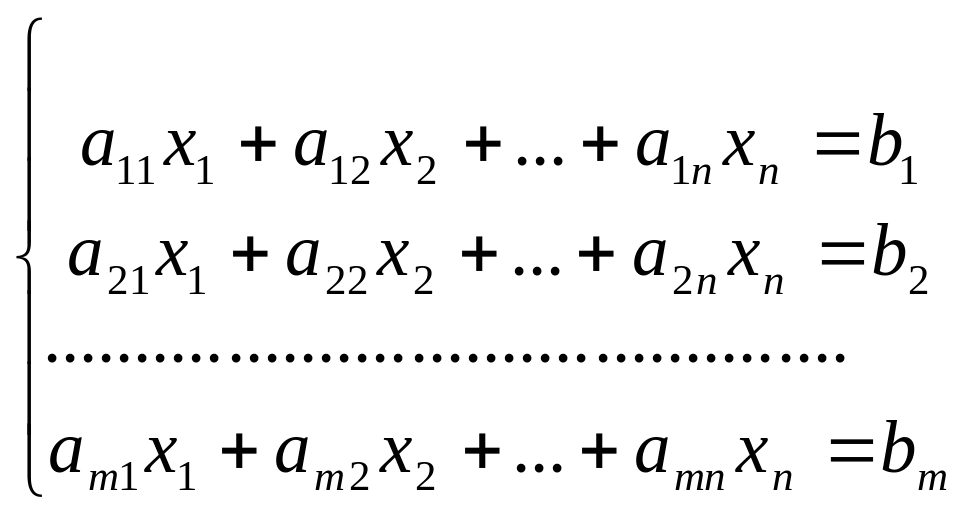
В общем виде система уравнений содержит m уравнений и n неизвестных. Коэффициенты при неизвестных имеют два индекса – первый индекс указывает номер уравнения, а второй – номер неизвестной. Коэффициенты b₁, b₂, …b_m, называются свободными элементами уравнений.

11. Решение системы линейных алгебраических уравнений методом Гаусса.

Метод Гаусса называют методом последовательного исключения неизвестных. Сущность метода заключается в том, что при помощи элементарных преобразований, таких как умножения (деления) любого уравнения системы на число и сложения с любым другим уравнением система приводится к треугольному виду. Последнее уравнение позволяет сделать заключение о совместности системы и, если система определенна, найти одно из неизвестных. Затем, двигаясь от последнего уравнения к первому (операции обратного хода), последовательно определяются все неизвестные системы.

Рассмотрим алгоритм метода Гаусса на примере решения системы уравнений.

В рассматриваемом примере коэффициенты при всех неизвестных отличны от единицы. Сделаем первое уравнение ведущим для исключения переменной х₁, для чего все уравнение разделим на коэффициент при х₁, который равен 2.

Ведущее уравнение запишем первым в системе

Из системы уравнений видно, что для исключения неизвестной х₁ из второго уравнения нужно первое уравнение умножить на (-2) и сложить со вторым. Для исключения неизвестной х₁ из третьего уравнения нужно первое уравнение умножить на (-4) и сложить с третьим.

В результате этих операций система уравнений будет иметь вид:

Теперь за ведущее примем второе уравнение и исключим неизвестную х₂ из третьего уравнения. Для этого второе уравнение нужно умножить на (-8) и сложить с третьим.

Будем иметь систему уравнений

Это были операции прямого хода. В результате исключения неизвестных х₁ и х₂ получена система треугольного вида.

Операции обратного хода.

Из последнего уравнения определяется ;

Из второго уравнения определяется ;

Из первого уравнения определяется .