Доверительный интервал для вероятности

Пусть случайная величина Х имеет только два возможных значения: 0 и 1. В результате проведения достаточно большого количества наблюдений эта случайная величина приняла единичное значение т раз. Необходимо при заданной надежности 1–  определить доверительный интервал для вероятности р, оценка которой соответствует частоте h = т/п.

Оценка h вероятности р является состоятельной, эффективной и несмещенной. Если оцениваемая вероятность не слишком мала и не слишком велика (0,05< p <0,95), то можно считать, что распределение случайной величины h близко к нормальному. Этим допущением можно пользоваться, если пр и п(1–р) больше четырех. Параметры нормального распределения частоты т₁ = р, т₂ = р(1–р)/п (дисперсия  ₂ (m) количества успехов т составляет величину пр(1–р), а дисперсия частоты  ₂(m)/п²). Тогда по аналогии с определением доверительного интервала для математического ожидания нормально распределенной величины h можно записать

Е = |h– p| = u _{1–  /2}( ₂(т) )^0,5 = u_{1–  /2}(р(1–р)/п)^0,5,

где u _{1–  /2} – квантиль стандартизованного нормального распределения.

Чтобы связать доверительный интервал с исходными параметрами n, h и u_{1–  /2}, возведем выражение для Е в квадрат, т. е. преобразуем равенство к виду (h–p)²=u²_{1–  /2}(1–p)p/п. Доверительные границы можно получить, решив это уравнение второй степени

p _{2, 1} ={nh + 0,5u²_{1–  /2}  u_{1–  /2} [nh(1–h) + 0,25u²_{1–  /2}]^0,5}/(п + u²_{1–  /2}).

№19 Проверка статистических гипотез.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой Р неизвестно полностью или частично. Тогда любое утверждение, касающееся Р называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение Р, то есть 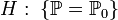, где Р₀ - какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения Р к некоторому семейству распределений, то есть вида 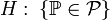, где 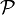- семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H₀. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H₁, называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения Р. В последовательном анализе выборка формируется в ходе самого эксперимента и потому ее объем является случайной величиной (см. Последовательный статистический критерий).

Этапы проверки статистических гипотез

1. Формулировка основной гипотезы H₀ и конкурирующей гипотезы H₁. Гипотезы должны быть чётко формализованы в математических терминах.

2. Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.

3. Расчёт статистики φ критерия такой, что:

   • её величина зависит от исходной выборки ;

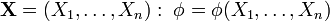   • по её значению можно делать выводы об истинности гипотезы H₀;

   • сама статистика φ должна подчиняться какому-то известному закону распределе-ния, т.к. сама φ является случайной в силу случайности .

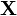4. Построение критической области. Из области значений φ выделяется подмно-жество С таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство 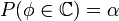. Это множество С и называется критической областью.

Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область С выносится решение об отвержении (или принятии) выдвинутой гипотезы H₀

№20 Проверка согласия опытного распределения с теоретическим на основе критерия Пирсона (критерия «хи-квадрат»)

Необходимость разработки настоящих рекомендаций вызвана следующими причинами.

Во-первых, в нормативных документах по стандартизации, устанавливающих правила проверки опытного распределения с теоретическим, нечетко определены правила применения критериев согласия типа χ² при проверке сложных гипотез. Некорректное использование оценок параметров по точечным (негруппированным) наблюдениям зачастую приводит к неоправданному отклонению проверяемой гипотезы.

Во-вторых, способы группирования наблюдений (способы разбиения области определения случайной величины на интервалы) при применении критериев типа χ² и выбор числа интервалов группирования не учитывают асимптотических свойств этих критериев. Неоднозначность процедуры группирования, неоптимальный выбор числа интервалов отражаются на мощности применяемого критерия, его способности различать близкие гипотезы, что, как правило, приводит к неоправданному принятию проверяемой гипотезы.

Настоящие рекомендации, с одной стороны, облегчают практическое применение критериев согласия типа χ², обеспечивают корректность статистических выводов, с другой стороны, содержат новые сведения из рассматриваемого раздела математической статистики.