7. Линейное векторное пространство: определение, свойства.

Векторным (линейным) пространством называется множество векторов (элементов) с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющим определенным аксиомам (свойствам)

1)х + у = у + х (перестановочность сложения);  2) (х + у) + z = x + (y + z) (ассоциативность сложения);  3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x;   4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,   5) 1 · х = х,   6) a(bx) = (ab) х (ассоциативность умножения);   7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя);   8) a(х + у) = aх + aу (распределительное свойство относительно векторного множителя).

Линейное пространство (векторное) V(P) над полем P – это непустое множество V. Элементы множества V называют векторами, а элементы поля P – скалярами.

Простейшие свойства.

1.Векторное пространство является абелевой группой(группа, в которой групповая операция является коммутативной. Групповая операция в абелевых группах обычно называется «сложением» и обозначается знаком +)

2.Нейтральный элемент является единственным, что вытекает из групповых свойств для любого .

3.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.

4.(–1) х = – х для любого х є V.

5.(–α) x = α(–x) = – (αx) для любых α є P и x є V.

Выражение a₁e₁ + a₂e₂ + … + a_ne_n   (1) называется линейной комбинацией векторов e₁, e₂,..., e_n с коэффициентами a₁, a₂,..., a_n. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a₁, a₂,..., a_n отличен от нуля. Векторы e₁, e₂,..., e_n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e₁, e₂,..., e_n равна нулевому вектору) векторы e₁, e₂,..., e_n называется линейно независимыми. Размерность пространства – максимальное число содержащихся в нем ЛЗ векторов.

Векторное пространство называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). Векторное пространство называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного Векторное пространство образуют базис этого пространства. Если e₁, e₂,..., e_n — базис Векторное пространство, то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: x = a₁e₁ + a₂e₂ +... + a_ne_n. При этом числа a₁, a_2,..., a_n называются координатами вектора х в данном базисе.

Векторное подпространство

Векторным подпространством, или просто подпространством, векторное пространство Е над полем К называется множество , замкнутое относительно действий сложения и умножения на скаляр. Подпространство, рассматриваемое отдельно от вмещающего его пространства, есть векторное пространство над тем же полем.

Множество называется подпространством линейного пространства V, если:

 1)

 2)

Евклидовы пространства. Для развития геометрических методов в теории Векторное пространство нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам х и у из R ставится в соответствие число, обозначаемое (х, у) и называемое скалярным произведением векторов х и у. При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения:   1) (х, у) = (у, х) (перестановочность);   2) (x₁ + x₂, y) = (x₁, y) + (x₂, y) (распределительное свойство);   3) (ax, у) = a(х, у),   4) (х, х) ³ 0 для любого х, причем (х, х) = 0 только для х = 0.   Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. Векторное пространство, в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством. 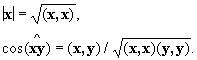Длина |x| вектора x и угол  между векторами х и у евклидова пространства определяются через скалярное произведение формулами     Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство Eⁿ получим, определяя в n-мepном арифметическом Векторное пространство скалярное произведение векторов x = (l₁, …, l_n) и y = (m₁, …, m_n) соотношением   (x, y) = l₁m₁ + l₂m₂ +… + l_nm_n.    (2)   При этом требования 1)—4), очевидно, выполняются.   В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: (х, у) = 0. В рассмотренном пространстве Eⁿ условие ортогональности векторов x = (l₁, …, l_n) и y = (m₁, …, m_n), как это следует из соотношения (2), имеет вид:   l₁m₁ + l₂m₂ +… + l_nm_n = 0. (3)